GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
This topic is relevant for:


Sketching Quadratic Graphs
Here we will learn about sketching quadratic graphs including how to identify key points on a graph of a quadratic function, and how to sketch quadratic graphs from these key points.
There are also quadratic graphs worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is sketching quadratic graphs?
Sketching quadratic graphs is slightly different to plotting quadratic graphs; a sketch of a graph shows the key points (see below) and the general shape of the graph, but is not expected to be as accurate as plotting a graph from a table of values.
A sketch of a graph wouldn’t be good enough to be able to estimate solutions to quadratic equations. However, a sketch is often useful in topics like solving quadratic inequalities, where knowing the general shape is important, but we don’t need to be really accurate.
Note that ‘sketch’ does not mean what it does in Art! A sketch of a graph should still be drawn with one smooth line or curve, and it’s good practice to use a ruler for the axes.
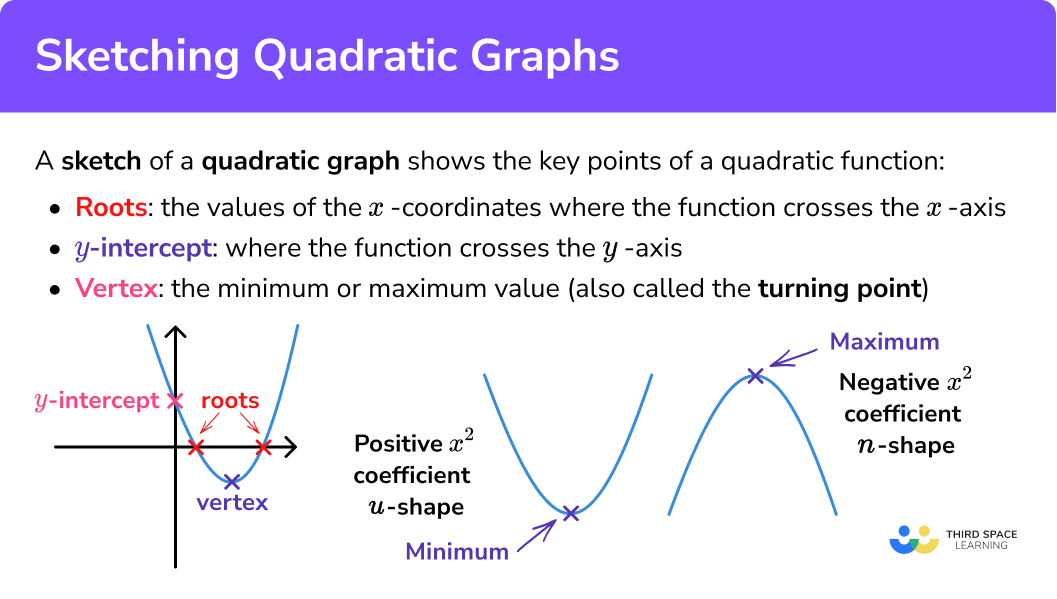
Key points on a quadratic graph
The graph of a quadratic function is always u-shaped (positive x^{2} coefficient) or n-shaped (negative x^{2} coefficient). Remember, ‘coefficient’ is just ‘the number in front of’.
The shape made by the graph of a quadratic function is called a parabola. It is symmetric, with the line or axis of symmetry running through the vertex.
The key points of a quadratic function are:
- The y -intercept;
- The vertex.
The roots of a quadratic function are the values of the x -coordinates where the function crosses the x -axis. They are sometimes called the x -intercepts.
A quadratic function will have zero, one (repeated), or two real roots.
When you solve a quadratic equation in the form ax^{2}+bx+c=0 , with the right-hand side equal to zero, you are finding the roots.
The y -intercept is where the function crosses the y -axis. You will have heard this phrase used before in graphs of straight lines – it is exactly the same here.
The vertex, sometimes called the turning point, of the graph, is the minimum or maximum value. A u-shaped quadratic has a minimum point, while a n-shaped quadratic has a maximum point.
How to sketch a quadratic graph
In order to sketch a quadratic graph:
Identify the coefficient of x^{2} , or ‘a’ ; this tells you whether the graph is u shaped or n shaped. Also identify the constant term, ‘c’ ; this tells you the y -intercept.
Set y=0 and solve the resulting quadratic equation to find the roots, or the x intercept(s).
Complete the square to find the coordinates of the vertex, then sketch the graph and label the key points.
Explain how to sketch a quadratic graph

Plotting quadratic graphs worksheet (includes sketching)
Get your free sketching quadratic graphs worksheet of 20+ plotting quadratic graphs questions and answers. Includes reasoning and applied questions.
Related lessons on quadratic graphs
Sketching quadratic graphs is part of our series of lessons to support revision on types of graphs . You may find it helpful to start with the main quadratic graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
- Types of graphs
- Quadratic graphs
- Plotting quadratic graphs
- Solving quadratic equations graphically
Sketching quadratic graphs examples
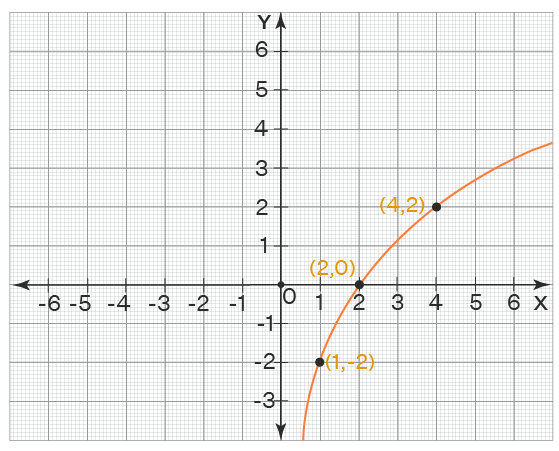
Example 1: a simple quadratic.
For the quadratic function y=x^{2}+2x , find the y -intercept, roots and vertex, and hence, sketch the graph.
Coefficient of x^{2} is (positive) 1 , so the graph is u shaped.
The constant term is 0 (there is no constant term), so the coordinates of the y -intercept are (0,0) .
2 Set y=0 and solve the resulting quadratic equation to find the roots, or the x intercept(s).
Solutions: x=0, x=−2 .
This quadratic function has two (real) roots, and crosses the x axis at x=−2, x=0.
3 Complete the square to find the coordinates of the vertex, then sketch the graph and label the key points.
x^{2}+2x=(x+1)^{2}-1
From this, the coordinates of the vertex are (−1,−1) (see Completing the Square for a step-by-step guide). This vertex is a minimum, because we’re dealing with a u shaped graph.
Sketch a set of axes, label each of the key points, then join with a smooth curve:
Example 2: a quadratic trinomial
For the quadratic function y=x^{2}+6x+5
Find the y -intercept, roots and vertex, and hence, sketch the graph.
The constant term is 5 , so the coordinates of the y -intercept are ( 0,5 ).
Solutions: x=−1, x=−5 .
This quadratic function has two (real) roots, and crosses the x axis at x=−1, x=−5 .
x^{2}+6x+5=(x+3)^{2}-4
The coordinates of the vertex are (−3,4) . This vertex is a minimum, because we’re dealing with a u shaped graph.
Example 3: another quadratic trinomial, estimated roots
For the quadratic function
y=4x-x^{2}+6
Coefficient of x^{2} is −1 , so the graph is n shaped.
The constant term is 6 , so the coordinates of the y -intercept are (0,6) .
0=4x-x^{2}+6
This does not factorise, so solve by completing the square or using the quadratic formula (see these pages for a full step-by-step guide):
Solutions: x=−1.16, x=5.16 (2d.p.)
This quadratic function has two (real) roots, and crosses the x axis at x=−1.16, x=5.16 (2d.p.) .
4x-x^{2}+6=-(x-2)^{2}+10
The coordinates of the vertex are (2,10) . This vertex is a maximum, because we’re dealing with a n shaped graph.
Sketch a set of axes, label each of the key points, then join with a smooth curve. When marking the roots on the x -axis, we can’t really be more accurate than 1 decimal place.
Example 4: a very challenging example
For the quadratic function y=5x-2x^{2}+7
Note: This is a challenging example, requiring many skills at a high level. Although it is unlikely (but not impossible!) that you would be asked a question this tricky at GCSE, if you are aiming for a Grade 8 or 9, you should be able to follow the steps in this example.
Coefficient of x^{2} is −2 , so the graph is n shaped.
The constant term is 7 , so the coordinates of the y -intercept are (0,7) .
Solutions:
This quadratic function has two (real) roots, and crosses the x axis at
The coordinates of the vertex are \left(\frac{5}{4}, \frac{81}{8}\right)
This vertex is a maximum because we’re dealing with a n shaped graph.
Common misconceptions
- Drawing a pointy vertex
Make sure that the vertex of the graph is a smooth curve, not pointed:
- Not using the coefficient of x^{2} to find the shape of the graph
Positive coefficient = u shaped
Negative coefficient = n shaped
Practice sketching quadratic graphs questions
1. Sketch the graph of y=x^{2}+4x

y intercept ( 0,0 ). Factorise to x(x+4) to get roots x=0 and x=-4 .
CTS (x+2)^{2}-4 gives vertex ( -2,-4 ).
Graph is a u shape because x^2 coefficient is positive.
2. Sketch the graph of y=x^{2}+2x-8
y intercept ( 0,-8 ).
Factorise to (x+4)(x-2) to get roots x=-4 and x=2 .
CTS (x+1)^{2}-9 gives vertex (-1,-9) .
3. Sketch the graph of y=-x^{2}+2x+3
y intercept (0,2) .
Factorise to (x+1)(3-x) to get roots x=-1 and x=3 .
CTS -(x-1)^{2}+4 gives vertex (1,4) .
Graph is a n shape because x^2 coefficient is negative.
4. Sketch the graph of y=4x^{2}-9
y intercept (0,-9) .
Factorise to (2x+3)(2x-3) (difference of two squares) to get roots x=-1.5 and x=1.5 .
In this case, because this is DOTS, we can’t complete the square, but we know the graph must be symmetrical about the y axis, so the vertex must be (0, -9) . Graph is a u shape because x^2 coefficient is positive.
Sketching quadratic graphs GCSE questions
(a) Show that x^{2}-4 x-12 can be written in the form (x-a)^{2}-b , where a and b are integers to be found. (b) Factorise x^{2}-4x-12 . (c) Hence, or otherwise, sketch the graph of the function y=x^{2}-4x-12 .
(x+ )(x- ) with two numbers that have a product of 12
Graph with vertex at (2,-16) and roots at x=-2,x=6
Fully correct U shaped graph
Learning checklist
You have now learned how to:
- Identify and interpret roots, intercepts and turning points of quadratic functions graphically
- Use the key points of a quadratic function to sketch its graph
The next lessons are
- Factorising
- Solving equations
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.
Privacy Overview

- Drawing Graphs of Functions
Steps for Sketching the Graph of the Function
Suppose we are given continuous on $$$ {\left[{a},{b}\right]} $$$ function $$$ y={f{{\left({x}\right)}}} $$$ that is twice differentiable, except points where the derivative $$$ f{'}\left({x}\right) $$$ doesn't exist or has infinite value.
To sketch the graph of a function, we need to perform the following:
- Determine, whether function is obtained by transforming a simpler function , and perform necessary steps for this simpler function.
- Determine, whether function is even, odd or periodic . This allows to draw graph of the function on some subinterval and then just reflect the result.
- Find y-intercept (point $$$ {f{{\left({0}\right)}}} $$$ ).
- Find x-intercepts (points where $$$ {f{{\left({x}\right)}}}={0} $$$ ).
- Find what asymptotes does function have, if any.
- Calculate first derivative and find points where $$$ {f{'}}{\left({x}\right)}={0} $$$ or $$$ {f{'}}{\left({x}\right)} $$$ doesn't exist, in other words find stationary points.
- Use a test ( the first derivative or the second derivative ) to classify stationary points.
- Find intervals where the function is increasing $$$ \left({f{'}}{\left({x}\right)}>{0}\right) $$$ and where it is decreasing $$$ \left({f{'}}{\left({x}\right)}<{0}\right) $$$ .
- Find points where $$$ {f{''}}{\left({x}\right)}={0} $$$ or $$$ {f{''}}{\left({x}\right)} $$$ doesn't exist and test whether these points are points of inflection .
- Find where function is concave up $$$ \left({f{''}}{\left({x}\right)}>{0}\right) $$$ and where it is concave down $$$ \left({f{''}}{\left({x}\right)}<{0}\right) $$$ .
- After you've found "important" points calculate corresponding values of function at these points.
- Add "control" points (some arbitrary points), if needed.
- Draw "important" and "control" points and connect them by lines taking into account found behavior of the function.
- If function is even, odd or periodic then perform corresponding reflection.
- If function is obtained by transforming simpler function, perform corresponding shift, compressing/stretching.
It is often convenient to draw all points, you've found, in the table.
Example 1 . Sketch graph of the function $$$ {f{{\left({x}\right)}}}=\frac{{1}}{{{x}-{1}}} $$$ .
Since $$$ {f{{\left({x}\right)}}}={g{{\left({x}-{1}\right)}}} $$$ where $$$ {g{{\left({x}\right)}}}=\frac{{1}}{{x}} $$$ then we study function $$$ {g{{\left({x}\right)}}}=\frac{{1}}{{x}} $$$ and then shift graph one unit to the right.
Function is odd because $$$ {g{{\left({x}\right)}}}=-{g{{\left(-{x}\right)}}} $$$ , so we consider only interval $$$ {\left[{0},\infty\right)} $$$ and then just reflect result about the origin. Function is not periodic.
There is no y-intercept because $$$ {g{{\left({0}\right)}}} $$$ is undefined.
There is no x-intercept because there are no points where $$$ {g{{\left({x}\right)}}}=\frac{{1}}{{x}}={0} $$$ .
Since $$$ \lim_{{{x}\to{{0}}^{+}}}\frac{{1}}{{x}}=+\infty $$$ then $$$ {x}={0} $$$ is vertical asymptote.
Since $$$ \lim_{{{x}\to\infty}}\frac{{1}}{{x}}={0} $$$ then $$$ {y}={0} $$$ is horizontal asymptote.
We have that $$$ {g{'}}{\left({x}\right)}=-\frac{{1}}{{{x}}^{{2}}} $$$ . There are no points where derivative equals 0. Point $$$ {x}={0} $$$ is where derivative doesn't exist.
Since $$$ {g{'}}{\left({x}\right)}=-\frac{{1}}{{{x}}^{{2}}}<{0} $$$ for all $$$ {x} $$$ then function is decreasing on $$$ {\left({0},+\infty\right)} $$$ and there are no extrema according to First Derivative Test.
Since second derivative is positive for $$$ {x}>{0} $$$ then function is concave upward on $$$ {\left({0},\infty\right)} $$$ .
Point $$$ {x}={0} $$$ is not point of inflection because $$$ {x}={0} $$$ is not in the domain of the function.
So, we actually don't have important points, but when $$$ {x} $$$ approaches 0 from the right function grows without a bound and we can sketch function, taking into account that functions is decreasing and concave upward on $$$ {\left({0},+\infty\right)} $$$ . For better graph take a couple of control points: $$$ {\left({1},{1}\right)},{\left({1},\frac{{1}}{{2}}\right)},{\left({4},\frac{{1}}{{4}}\right)} $$$ .
Since function is odd, reflect it about origin.
Shift the function 1 unit to the right.
Example 2 . Sketch graph of the function $$$ {f{{\left({x}\right)}}}={{\left({x}+{2}\right)}}^{{2}}{{\left({x}-{1}\right)}}^{{3}} $$$ .
There is no simpler function that initial function is obtained from.
Function is neither even nor odd and not periodic.
$$$ {f{{\left({0}\right)}}}={{\left({0}+{2}\right)}}^{{2}}{{\left({0}-{1}\right)}}^{{3}}=-{4} $$$ , so y-intercept is -4.
x-intercepts are points where $$$ {f{{\left({x}\right)}}}={0} $$$ : $$$ {{\left({x}+{2}\right)}}^{{2}}{{\left({x}-{1}\right)}}^{{3}}={0} $$$ which gives $$$ {x}=-{2} $$$ and $$$ {x}={1} $$$ .
Since function is continuous everywhere, $$$ \lim_{{{x}\to-\infty}}{f{{\left({x}\right)}}}=-\infty $$$ and $$$ \lim_{{{x}\to\infty}}{f{{\left({x}\right)}}}=\infty $$$ then there are no asymptotes.
We have that $$$ {f{'}}{\left({x}\right)}={2}{\left({x}+{2}\right)}{{\left({x}-{1}\right)}}^{{3}}+{3}{{\left({x}+{2}\right)}}^{{2}}{{\left({x}-{1}\right)}}^{{2}}={\left({x}+{2}\right)}{{\left({x}-{1}\right)}}^{{2}}{\left({2}{x}-{2}+{3}{x}+{6}\right)}= $$$
$$$ ={\left({x}+{2}\right)}{{\left({x}-{1}\right)}}^{{2}}{\left({5}{x}+{4}\right)} $$$ .
So, derivative equals 0 when $$$ {x}=-{2},{x}={1},{x}=-\frac{{4}}{{5}} $$$ .
According to method of intervals number line is divided by stationary points on four intervals.
First interval is $$$ {\left(-\infty,-{2}\right)} $$$ : taking any point from this interval, for example $$$ {x}=-{3} $$$ we obtain that $$$ {f{'}}{\left(-{3}\right)}={\left(-{3}+{2}\right)}{{\left(-{3}-{1}\right)}}^{{2}}{\left({5}\cdot{\left(-{3}\right)}+{4}\right)}>{0} $$$ , so $$$ {f{'}}{\left({x}\right)}>{0} $$$ on this interval.
Second interval is $$$ {\left(-{2},-\frac{{4}}{{5}}\right)} $$$ : taking any point from this interval, for example $$$ {x}=-{1} $$$ we obtain that $$$ {f{'}}{\left(-{1}\right)}={\left(-{1}+{2}\right)}{{\left(-{1}-{1}\right)}}^{{2}}{\left({5}\cdot{\left(-{1}\right)}+{4}\right)}<{0} $$$ , so $$$ {f{'}}{\left({x}\right)}<{0} $$$ on this interval.
Third interval is $$$ {\left(-\frac{{4}}{{5}},{1}\right)} $$$ : taking any point from this interval, for example $$$ {x}={0} $$$ we obtain that $$$ {f{'}}{\left({0}\right)}={\left({0}+{2}\right)}{{\left({0}-{1}\right)}}^{{2}}{\left({5}\cdot{\left({0}\right)}+{4}\right)}>{0} $$$ , so $$$ {f{'}}{\left({x}\right)}>{0} $$$ on this interval.
Fourth interval is $$$ {\left({1},\infty\right)} $$$ : taking any point from this interval, for example $$$ {x}={3} $$$ we obtain that $$$ {f{'}}{\left({3}\right)}={\left({3}+{2}\right)}{{\left({3}-{1}\right)}}^{{2}}{\left({5}\cdot{3}+{4}\right)}>{0} $$$ , so $$$ {f{'}}{\left({x}\right)}>{0} $$$ on this interval.
Second derivative is $$$ {f{''}}{\left({x}\right)}={2}{\left({x}-{1}\right)}{\left({10}{{x}}^{{2}}+{16}{x}+{1}\right)} $$$ .
Roots of the equation $$$ {10}{{x}}^{{2}}+{16}{x}+{1}={0} $$$ are $$$ {x}=\frac{{-{8}+{3}\sqrt{{{6}}}}}{{10}}\approx-{0.065} $$$ and $$$ {x}=\frac{{-{8}-{3}\sqrt{{{6}}}}}{{10}}\approx-{1.535} $$$ .
So, points where second derivative equals 0 are $$$ {x}={1},{x}=-{0.065},{x}=-{1.535} $$$ .
Clearly they are all points of inflections because second derivative changes sign at these points.
$$$ {f{''}}{\left({x}\right)}>{0} $$$ on $$$ {\left(-{1.535},-{0.065}\right)}\cup{\left({1},\infty\right)} $$$ and $$$ {f{''}}{\left({x}\right)}<{0} $$$ on $$$ {\left(-\infty,-{1.535}\right)}\cup{\left(-{0.0065},{1}\right)} $$$ .
So we have following "important" points:
| $$${x}$$$ | -2 | -1.535 | $$$-\frac{{4}}{{5}}$$$ | -0.065 | 0 | 1 |
| $$${f{{\left({x}\right)}}}$$$ | 0 | -3.52241 | -8.3981 | -4.052 | -4 | 0 |
| type | maximum, x-intercept | inflection | minimum | inflection | y-intercept | inflection, x-intercept |
Function is increasing on $$$ {\left(-\infty,-{2}\right)}\cup{\left(-\frac{{4}}{{5}},\infty\right)} $$$ and decreasing on $$$ {\left(-{2},-\frac{{4}}{{5}}\right)} $$$ .
Function is concave upward on $$$ {\left(-{1.535},-{0.065}\right)}\cup{\left({1},\infty\right)} $$$ and concave downward on $$$ {\left(-\infty,-{1.535}\right)}\cup{\left(-{0.0065},{1}\right)} $$$ .
Note that points $$$ {\left(-{0.065},-{4.052}\right)} $$$ and $$$ {\left({0},-{4}\right)} $$$ are very close, so they are almost indistinguishable on graph.
Example 3 . Sketch graph of the function $$$ {f{{\left({x}\right)}}}=\frac{{{{x}}^{{2}}-{5}{x}+{6}}}{{{{x}}^{{2}}+{1}}} $$$ .
$$$ {f{{\left({0}\right)}}}=\frac{{{{0}}^{{2}}-{5}\cdot{0}+{6}}}{{{{0}}^{{2}}+{1}}}={6} $$$ , so y-intercept is 6.
x-intercepts are points where $$$ {f{{\left({x}\right)}}}={0} $$$ : $$$ {\left({{x}}^{{2}}-{5}{x}+{6}\right)}={\left({x}-{2}\right)}{\left({x}-{3}\right)}={0} $$$ which gives $$$ {x}={2} $$$ and $$$ {x}={3} $$$ .
Since function is continuous everywhere, $$$ \lim_{{{x}\to\infty}}\frac{{{{x}}^{{2}}-{5}{x}+{6}}}{{{{x}}^{{2}}+{1}}}={1} $$$ then there is only one asymptote: horizontal asymptote $$$ {y}={1} $$$ .
We have that $$$ {f{'}}{\left({x}\right)}=\frac{{{\left({{x}}^{{2}}-{5}{x}+{6}\right)}'{\left({{x}}^{{2}}+{1}\right)}-{\left({{x}}^{{2}}-{5}{x}+{6}\right)}{\left({{x}}^{{2}}+{1}\right)}'}}{{{\left({{x}}^{{2}}+{1}\right)}}^{{2}}}={5}\frac{{{{x}}^{{2}}-{2}{x}-{1}}}{{{\left({{x}}^{{2}}+{1}\right)}}^{{2}}} $$$ .
Roots of the equation $$$ {{x}}^{{2}}-{2}{x}-{1}={0} $$$ are $$$ {x}={1}+\sqrt{{{2}}}\approx{2.41} $$$ and $$$ {x}={1}-\sqrt{{{2}}}\approx-{0.41} $$$ .
So, derivative equals 0 when $$$ {x}=-{0.41},{x}={2.41} $$$ .
According to method of intervals number line is divided by stationary points on three intervals.
First interval is $$$ {\left(-\infty,-{0.41}\right)} $$$ : $$$ {f{'}}{\left({x}\right)}>{0} $$$ on this interval.
Second interval is $$$ {\left(-{0.41},{2.41}\right)} $$$ : $$$ {f{'}}{\left({x}\right)}<{0} $$$ on this interval.
Third interval is $$$ {\left({2.41},\infty\right)} $$$ : $$$ {f{'}}{\left({x}\right)}>{0} $$$ on this interval.
Second derivative is $$$ {f{''}}{\left({x}\right)}=-{10}\frac{{{\left({x}+{1}\right)}{\left({{x}}^{{2}}-{4}{x}+{1}\right)}}}{{{\left({{x}}^{{2}}+{1}\right)}}^{{3}}} $$$ .
Roots of the equation $$$ {{x}}^{{2}}-{4}{x}+{1}={0} $$$ are $$$ {x}={2}-\sqrt{{{3}}}\approx{0.27} $$$ and $$$ {x}={2}+\sqrt{{{3}}}\approx{3.73} $$$ .
So, points where second derivative equals 0 are $$$ {x}=-{1},{x}={0.27},{x}={3.73} $$$ .
$$$ {f{''}}{\left({x}\right)}>{0} $$$ on $$$ {\left(-\infty,-{1}\right)}\cup{\left({0.27},{3.73}\right)} $$$ and $$$ {f{''}}{\left({x}\right)}<{0} $$$ on $$$ {\left(-{1},{0.27}\right)}\cup{\left({3.73},\infty\right)} $$$ .
| $$${x}$$$ | -1 | -0.41 | 0 | 0.27 | 2 | 2.41 | 3 | 3.73 |
| $$${f{{\left({x}\right)}}}$$$ | 6 | 7.0354 | 6 | 4.402 | 0 | -0.0355 | 0 | 0.0847 |
| type | inflection | maximum | y-intercept | inflection | x-intercept | minimum | x-intercept | inflection |
Function is increasing on $$$ {\left(-\infty,-{0.41}\right)}\cup{\left({2.41},\infty\right)} $$$ and decreasing on $$$ {\left(-{0.41},{2.41}\right)} $$$ .
Function is concave upward on $$$ {\left(-\infty,-{1}\right)}\cup{\left({0.27},{3.73}\right)} $$$ and concave downward on $$$ {\left(-{1},{0.27}\right)}\cup{\left({3.73},\infty\right)} $$$ .
Horizontal asymptote is $$$ {y}={1} $$$ .
Example 4 . Sketch graph of the function $$$ {f{{\left({x}\right)}}}=\frac{{{\left({x}-{1}\right)}}^{{3}}}{{{\left({x}+{1}\right)}}^{{2}}} $$$ .
$$$ {f{{\left({0}\right)}}}=\frac{{{\left({0}-{1}\right)}}^{{3}}}{{{\left({0}+{1}\right)}}^{{2}}}=-{1} $$$ , so y-intercept is -1.
x-intercepts are points where $$$ {f{{\left({x}\right)}}}={0} $$$ : $$$ {{\left({x}-{1}\right)}}^{{3}}={0} $$$ which gives $$$ {x}={1} $$$ .
Vertical asymptote is $$$ {x}=-{1} $$$ because $$$ \lim_{{{x}\to-{{1}}^{+}}}\frac{{{\left({x}-{1}\right)}}^{{3}}}{{{\left({x}+{1}\right)}}^{{2}}}=-\infty $$$ .
There are no horizontal asymptotes because $$$ \lim_{{{x}\to\infty}}\frac{{{\left({x}-{1}\right)}}^{{3}}}{{{\left({x}+{1}\right)}}^{{2}}}=\infty $$$ and $$$ \lim_{{{x}\to-\infty}}\frac{{{\left({x}-{1}\right)}}^{{3}}}{{{\left({x}+{1}\right)}}^{{2}}}=-\infty $$$ .
Since $$$ \lim_{{{x}\to\infty}}\frac{{{f{{\left({x}\right)}}}}}{{x}}=\lim_{{{x}\to\infty}}\frac{{{{x}}^{{3}}-{3}{{x}}^{{2}}+{3}{x}-{1}}}{{{{x}}^{{3}}+{2}{{x}}^{{2}}+{x}}}={1} $$$ then $$$ {m}={1} $$$ . Now $$$ \lim_{{{x}\to\infty}}{\left({f{{\left({x}\right)}}}-{m}{x}\right)}=\frac{{{{x}}^{{3}}-{3}{{x}}^{{2}}+{3}{x}-{1}}}{{{{x}}^{{2}}+{2}{x}+{1}}}-{x}=\lim_{{{x}\to\infty}}\frac{{-{5}{{x}}^{{2}}+{2}{x}-{1}}}{{{{x}}^{{2}}-{2}{x}+{1}}}=-{5} $$$ .
So, there is slant asymptote $$$ {y}={x}-{5} $$$ .
We have that $$$ {f{'}}{\left({x}\right)}=\frac{{{\left({{\left({x}-{1}\right)}}^{{3}}\right)}'{{\left({x}+{1}\right)}}^{{2}}-{{\left({x}-{1}\right)}}^{{3}}{\left({{\left({x}+{1}\right)}}^{{2}}\right)}'}}{{{\left({x}+{1}\right)}}^{{4}}}=\frac{{{{\left({x}-{1}\right)}}^{{2}}{\left({x}+{5}\right)}}}{{{\left({x}+{1}\right)}}^{{3}}} $$$ .
Derivative equals 0 when $$$ {x}={1},{x}=-{5} $$$ and doesn't exist when $$$ {x}=-{1} $$$ .
Since $$$ {{\left({x}-{1}\right)}}^{{2}}\ge{0} $$$ then these factor doesn't influence sign of derivative.
Thus $$$ {f{'}}{\left({x}\right)}>{0} $$$ when $$$ {x}\in{\left(-\infty,-{5}\right)}\cup{\left(-{1},\infty\right)} $$$ and $$$ {f{'}}{\left({x}\right)}<{0} $$$ when $$$ {x}\in{\left(-{5},-{1}\right)} $$$ .
Point $$$ {x}=-{1} $$$ is not in the domain of function, so clearly not an extremum.
Second derivative is $$$ {f{''}}{\left({x}\right)}={24}\frac{{{x}-{1}}}{{{\left({x}+{1}\right)}}^{{4}}} $$$ .
So, point where second derivative equals 0 is $$$ {x}={1} $$$ .
Clearly it is inflection point because second derivative changes sign at this point.
$$$ {f{''}}{\left({x}\right)}>{0} $$$ when $$$ {x}>{1} $$$ and $$$ {f{''}}{\left({x}\right)}<{0} $$$ when $$$ {x}<{1} $$$ .
Let's add a couple of control points:
$$$ {x}={3} $$$ , $$$ {f{{\left({3}\right)}}}={0.5} $$$ .
$$$ {x}=-{8} $$$ , $$$ {f{{\left(-{8}\right)}}}\approx-{14.88} $$$ .
So, we have following points:
| $$${x}$$$ | -8 | -5 | 0 | 1 | 3 |
| $$${f{{\left({x}\right)}}}$$$ | -14.88 | -13.5 | -1 | 0 | 0.5 |
| type | control | maximum | y-intercept | inflection | control |
Function is increasing on $$$ {\left(-\infty,-{5}\right)}\cup{\left(-{1},\infty\right)} $$$ and decreasing on $$$ {\left(-{5},-{1}\right)} $$$ .
Function is concave upward on $$$ {\left({1},\infty\right)} $$$ and concave downward on $$$ {\left(-\infty,{1}\right)} $$$ .
Vertical asymptote is $$$ {x}=-{1} $$$ and slant asymptote is $$$ {y}={x}-{5} $$$ .
- < Introduction to Sketching Graph of Function

- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
How to Sketch the Graph of a Function – Easy Steps for Beginners
JUMP TO TOPIC
Steps Involved in Sketching Graph of a Function
Exploring sketch features, function types and characteristics.

To sketch the graph of a function, I first consider the type of function and its features, such as intercepts, slopes, and asymptotes.
Drawing the graph of a function is a practical way to visualize the behavior of mathematical expressions over a given domain.
When I analyze the graph of a function , I look for key information that indicates how the function behaves across different intervals. This includes finding the zeros, the increases and decreases, and any points of discontinuity.
My strategy involves plotting known points, particularly where the function intersects the axes. For functions like polynomials, this may involve solving for when the function equals zero.
I then determine the interval over which I’m interested in the function’s behavior, whether it’s a specific range or a broader perspective.
Finally, I check for symmetry and other patterns that might simplify my sketch, ensuring my graph is comprehensive and accurate. By approaching the sketch methodically and considering these elements, I gain a complete picture of the function’s characteristics.
When I begin to sketch the graph of a function , I first consider its domain and range .
The domain represents all possible input values (usually the x -values), which are the real numbers that can be plugged into the function without causing any undefined behavior.
For example, in the function $f(x) =2x-1$, the domain excludes the value $x = 1$ because it would make the denominator zero, which is undefined.
I then locate any asymptotes , which are lines the graph approaches but never touches. Vertical asymptotes often occur where the denominator of a rational function is zero, and horizontal asymptotes are linked to the behavior of the function as $x$ approaches infinity.
The slope of the function helps me understand how steep the graph is. For a linear function , the slope is constant, while for non-linear functions , the slope changes as $x$ changes.
When graphing, I use transformations such as reflection , shift , or stretching to adjust the basic graph of the function . A graphing calculator can be extremely helpful in this process, offering a visual representation of the function .
Identifying any critical points , such as local maxima and minima, and inflection points where the concavity changes, is also important. They give me detailed information about the function ‘s behavior and help refine my sketch.
Here’s a quick reference table summarizing the steps:
| Step | Description |
|---|---|
| and | Determine acceptable and values |
| Set $x = 0$ in the | |
| Solve $f(x) = 0$ | |
| Look for values that make the undefined | |
| and Curvature | Analyze changes to plot the curve |
| Transformations | Apply and to alter the basic |
| Critical Points | Find and plot maxima, minima, and |
With these steps, I’m equipped to create an accurate and detailed graph of most functions .
When I begin sketching a graph, I find it immensely helpful to identify the essential characteristics of a function. These features help predict the appearance of the graph before I even put pen to paper.
Intervals of increase and decrease inform me about the slope of a function. In parts where a function is increasing , the graph moves upward as it goes from left to right, and when it’s decreasing , it slopes downward.
The points where a graph changes from increasing to decreasing or vice versa are known as critical points . These points often correspond to local extrema , which are the highs and lows of the graph.
Inflection points are also key: They are where the graph changes concavity, shifting between concave up (shaped like a cup) and concave down (shaped like a cap). ‘
A concise way to remember is that when a graph is concave up , the derivative is increasing, and when it’s concave down , the derivative is decreasing.
Finally, a snapshot of the end behavior can be taken by looking at what happens to the graph as ( x ) approaches infinity or negative infinity. Does it level off, or does it escape off to infinity? The answers give clues to the tails of the graph.
Here’s a quick reference table summarizing these features:
| Feature | Description | Impact on Graph |
|---|---|---|
| Regions where the function’s slope is positive/negative | Slope direction | |
| Where the first derivative is zero or undefined | Potential local | |
| Where concavity changes | Slope curvature change | |
| As ( x ) approaches ( \pm \infty ) | Tail direction |
By meticulously analyzing these characteristics, I can sketch a more accurate representation of any function.
When I explore different types of functions , I first understand their characteristics and behavior. For instance, a linear function like ( f(x) = mx + b ) has a constant rate of change, known as the slope ( m ), and a y-intercept ( b ).
The graph is a straight line with slope ( m ) and y-intercept ( b ).
Moving on to polynomial functions , these can be expressed in the form $ f(x) = a_n x^n + a_{n-1} x^{n-1} + … + a_1 x + a_0 $, where ( n ) is the degree of the polynomial.
Notably, if ( n ) is even, the polynomial function can have a similar end behavior on both sides, while an odd-degree polynomial tends to have opposite end behaviors. Rational functions are formed by the quotient of two polynomials, like $ f(x) = \frac{p(x)}{q(x)} $.
They may have horizontal asymptotes , which I locate by comparing the degrees of the numerator and denominator polynomials. When the degree of the numerator is less than the denominator, the x-axis (y = 0) is typically the horizontal asymptote.
Transcendental functions include exponential , logarithmic , and trigonometric functions . These do not have a degree like polynomials but have their unique properties. For example, the exponential function $f(x) = e^x$ grows rapidly, and its derivative is itself.
To determine the nature of turning points or concavity, I utilize the first and second derivative tests.
Through the derivative , I identify critical points and use the second derivative to determine if the function is concave up (positive second derivative) or concave down (negative second derivative).
| Type | Definition | Characteristics |
|---|---|---|
| Linear | $f(x) = mx + b$ | Constant rate of change, straight line graph |
| Polynomial | $ f(x) = a_n x^n + … + a_0$ | Degree determines end behavior |
| Rational | $f(x) = \frac{p(x)}{q(x)}$ | May have horizontal asymptotes |
| Transcendental | $f(x) = e^x$ , etc. | Unique properties, not defined by a degree |
In summary, understanding these characteristics helps me sketch the curves accurately, predict their behavior, and analyze their properties more effectively.
In this guide, I’ve walked you through the steps to sketch the graph of a function efficiently. Remember, practice makes perfect.
The more functions you graph, the better intuition you’ll develop for their behavior. Use the domain , intercepts , and end behavior to establish a framework for your graph.
Techniques such as testing for even , odd , or periodic properties can simplify your work by revealing symmetries.
Always start with a clear understanding of the domain of your function, which reveals the possible x-values you can input. The intercepts give you specific points where the graph crosses the axes, with the x-intercepts found by solving the equation ( f(x) = 0 ) and the y-intercept by evaluating ( f(0) ).
For the end behavior , investigate the limits as ( x ) approaches infinity and negative infinity to determine horizontal asymptotes, if they exist. If a function approaches a particular y-value ( L ) as ( x ) grows large, you can denote this with a horizontal line ( y = L ).
By following these methods, I hope you feel more confident in your graphing skills. Keep your pencil moving, and look for patterns and relationships in the functions you plot.
- Pre Calculus
- Probability
- Sets & Set Theory
- Trigonometry
Graphing Functions
Graphing functions is the process of drawing the graph (curve) of the corresponding function. Graphing basic functions like linear, quadratic, cubic, etc is pretty simple, graphing functions that are complex like rational, logarithmic, etc, needs some skill and some mathematical concepts to understand.
Let us see the process of graphing functions along with examples.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What is Meant By Graphing Functions?
Graphing functions is drawing the curve that represents the function on the coordinate plane. If a curve (graph) represents a function, then every point on the curve satisfies the function equation. For example, the following graph represents the linear function f(x) = -x+ 2.
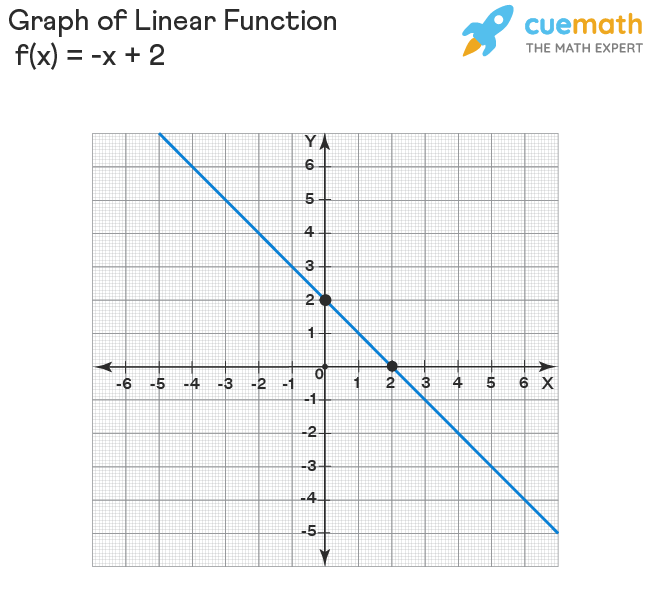
Take any point on this line, say, (-1, 3). Let us substitute (-1, 3) = (x, y) (i.e., x = -1 and y = 3) in the function f(x) = -x + 2 (note that it can be written as y = -x + 2). Then
3 = -(-1) + 2 3 = 1 + 2 3 = 3, thus, (-1, 3) satisfies the function.
In the same way, you can try taking different points and checking whether they satisfy the function. Each and every point on the line (in general called "curve") satisfies the function. Drawing such curves representing the functions is known as graphing functions.
Graphing Basic Functions
Graphing basic functions like linear functions and quadratic functions is easy. The basic idea of graphing functions is
- Identifying the shape if possible. For example, if it is a linear function of the form f(x) = ax + b, then its graph would be a line; if it is a quadratic function of the form f(x) = ax 2 + bx + c, then its a parabola .
- finding some points on it, by substituting some random values of x and finding the corresponding values of y by substituting each value into the function .
Here are some examples.
Graphing Linear Functions
Let us graph the same linear function as mentioned in the previous section (f(x) = -x + 2). For this, we create a table of values by taking some random numbers for x say x = 0 and x = 1. Then substitute each of these in y = -x + 2 to compute y-values.
| x | y |
|---|---|
| 0 | -0 + 2 = 2 |
| 1 | -1 + 2 = 1 |
Thus, two points on the line are (0, 2) and (1, 1). If we plot them on a graph and join them by a straight line (extending the line on both sides), we get its graph as shown in the previous section.
Graphing Quadratic Functions
For graphing quadratic function also, we can find some random points on it. But this may not give a perfect U-shaped curve. This is because, to get a perfect U-shaped curve, we need where the curve is turning. i.e., we have to find its vertex . After finding the vertex, we can find two or three random points on each side of the vertex and they would help in graphing the function.
Example: Graph the quadratic function f(x) = x 2 - 2x + 5.
Comparing it with f(x) = ax 2 + bx + c, a = 1, b = -2, and c = 5.
The x-coordinate of the vertex is, h = -b/2a = -(-2)/2(1) = 1.
Its y-coordinate is, f(1) = 1 2 - 2(1) + 5 = 4.
Hence, the vertex is (1, 4).
We will take two random numbers on each side of 1 (which is the x-coordinate of the vertex) and frame a table. Then we can calculate the y-coordinates using the function.
| x | y |
|---|---|
| -1 | (-1) - 2(-1) + 5 = 8 |
| 0 | 0 - 2(0) + 5 = 5 |
| Vertex: 1 | 4 |
| 2 | 2 - 2(2) + 5 = 5 |
| 3 | 3 - 2(3) + 5 = 8 |
Now, we will plot the points (-1, 8), (0, 5), (1, 4), (2, 5), and (3, 8) on a graph sheet, join them, and extend the curve on both sides.

Graphing Complex Functions
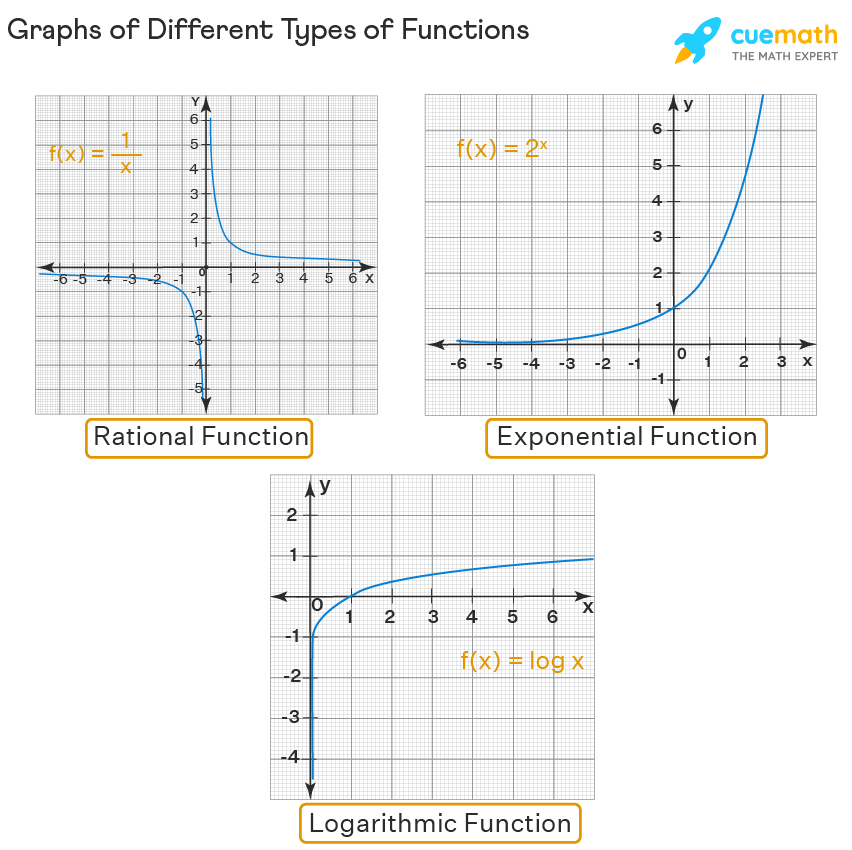
Graphing functions is comparably simple if each of their domain and range is the set of all real numbers. But it is NOT the case with all types of functions. There are some complex functions for which domain, range, asymptotes, and holes have to be taken care of while graphing them. The most popular such functions are:
- Rational functions - Its parent function is of the form f(x) = 1/x (which is called the reciprocal function).
- Exponential functions - Its parent function is of the form f(x) = a x .
- Logarithmic Functions - Its parent function is of the form f(x) = log x.
Just have an idea of what the graphs of parent functions of each of these functions look like.
In each of these cases, for graphing functions , we follow the following steps:
- Find the domain and range of the function and keep it in mind while drawing the curve.
- Find x-intercept (s) and y-intercept (s), and plot them.
- Identify the holes if any.
- Find the asymptotes ( vertical , horizontal , and slant ) and draw them by dotted lines so that we can break the graph along those lines and make sure that the graph doesn't touch them.
- Construct a table of values by taking some random numbers for x (on both sides of x-intercept and/or on both sides of the vertical asymptote), calculate the corresponding values of y.
- Plot the points from the table, and join them by taking care of asymptotes, domain, and range.
Let us see how to graph a function in different cases using the above steps.
Graphing Rational Functions
Let us graph a rational function f(x) = (x + 1) / (x - 2). We follow the above steps and graph this function.
- Domain = {x ∈ R | x ≠ 2} ; Range = {y ∈ R | y ≠ 1}. To understand how to find the domain and range of a rational function, click here .
- Its x-intercept is (-1, 0) and y-intercept is (0, -0.5).
- There are no holes.
- Vertical asymptote (VA) is x = 2 and horizontal asymptote (VA) is y = 1.
| x | y |
|---|---|
| -1 | (-1+1)/(-1-2) = 0 (x-int) |
| 0 | (0+1)/(0-2) = -0.5 (y-int) |
| 2 | VA |
| 3 | (3+1)/(3-2) = 4 |
| 4 | (4+1)/(4-2) = 2.5 |

Graphing Exponential Functions
Consider an exponential function f(x) = 2 -x + 2. We will graph it using the same steps as mentioned above.
- Its domain is the set of all real numbers (R) and its range is y > 2. To know how to find these, click here .
- It has no vertical asymptotes. But it has a horizontal asymptote at y = 2.
- It has no x-intercepts. Its y-intercept is (0, 3).
| x | y |
|---|---|
| -2 | 2 + 2 = 6 |
| -1 | 2 + 2 = 4 |
| 0 | 3 (y-int) |
| 1 | 2 + 2 = 2.5 |
| 2 | 2 + 2 = 2.25 |

Graphing Logarithmic Functions
We will graph a logarithmic function, say f(x) = 2 log 2 x - 2. We will graph it now by following the steps as explained earlier.
- Its domain is x > 0 and its range is the set of all real numbers (R). To understand this, click here .
- Its x-int is (2, 0) and there is no y-int.
- Its vertical asymptote is y = 0 (x-axis) and no horizontal asymptote.
| x | y |
|---|---|
| 1 | 2 log 1 - 2 = -2 |
| 2 | 0 (x-int) |
| 4 | 2 log 4 - 2 = 2 |
Note that we have chosen such numbers for x that are easy to simplify the y-values.
Similarly, you can see how to graph non-linear functions , identity function , modulus function , polynomial functions , zero function , greatest integer function , constant function , trigonometric functions , fractional part function , etc, by clicking on the respective links.
Graphing Functions by Transformations
We can graph the functions by applying transformations on the graphs of the parent functions. Here are the parent functions of a few important types of functions.
- Linear function : f(x) = x
- Quadratic function : f(x) = x 2
- Cubic functions : f(x) = x 3
- Square root function : f(x) = √x
- Cube root function : f(x) = ∛x
- Absolute value function : f(x) = |x|
- Reciprocal function : f(x) = 1/x
- Exponential function : f(x) = a x , 0 < a < 1
- Logarithmic function: f(x) = log x
We need to have an idea about how the graph of each of these parent functions looks like (by clicking on the respective links). Then we can apply the following transformations to graph the given function.
| Transformation | Change in Graph |
|---|---|
| f(x) + c | It shifts the graph of the function c units upward. |
| f(x) - c | It shifts the graph of the function c units downward. |
| f(x + c) | It shifts the graph of the function c units to the left. |
| f(x - c) | It shifts the graph of the function c units to the right. |
| -f(x) | It reflects the graph of the function in the x-axis (upside down). |
| f(-x) | It reflects the graph of the function in the y-axis (i.e., the left and right sides are swapped). |
| f(ax) | Horizontal dilation by a factor of 1/a. |
| a f(x) | Vertical dilation by a factor of a. |
To understand how to graph the functions by using transformations in detail, click here .
Important Notes on Graphing Functions:
- f(ax) ≠ a f(x). Both may have different values.
- The value of x used to plot any function f(x) can be a whole number , real number , or decimal number .
- The graph of a function should never touch the asymptotes.
- Do not choose the values of x in the table that are NOT there in the domain of the function.
☛ Related Topics:
- Graphing Functions Calculator
- Introduction to Graphing
- Visualizing Functions Through Graphs
Graphing Functions Examples
Example 1: Determine which of the following points lie on the graph of function f(x) = 2x 3 - 2? (a) (1, 1) (b) (1, 0) (c) (2, 6).
We will substitute each point in the given function to see which of them satisfies the function.
(a) (1, 1) = (x, f(x))
1 = 2(1) 3 - 2 1 = 2 - 2 1 = 0, not satisfied
So (1, 1) is NOT on the graph of the function.
(b) (1, 0) = (x, f(x))
0 = 2(1) 3 - 2 0 = 2 - 2 0 = 0, satisfied
So (1, 1) is on the graph of the function.
(c) (2, 6) = (x, f(x))
6 = 2(2) 3 - 2 6 = 16 - 2 6 = 14, not satisfied
So (2, 6) is NOT on the graph of the function.
Answer: Only (b) lies on the given function.
Example 2: Does the graph given in Example 1 has any asymptotes? Explain. How many parts does it have?
The given function is f(x) = 2x 3 - 2, which is a polynomial function and hence it has no asymptotes.
When there are no asymptotes, we will get only one curve (as the curve doesn't break anywhere) while graphing functions.
Answer: No asymptotes and only one curve.
Example 3: Draw the graph of the function given in Example 1 along with the point(s) you found from its solution.
In Example 1 , we have already found that (1, 0) lies on the function f(x) = 2x 3 - 2. For graphing functions, we need more points. Let us construct a table for the same.
| x | y |
|---|---|
| -1 | 2(-1) - 2 = -4 |
| 0 | 2(0) - 2 = -2 |
Let us plot these points along with (1, 0) and plot it.
Answer: The graph is drawn.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Graphing Functions
go to slide go to slide
FAQs on Graphing Functions
How to graph functions.
For graphing functions , we need to plot its asymptotes, its x and y-intercepts, holes, and a few points on it by constructing a table of values. Then just join the point by not touching the asymptotes and keeping a note of the domain and range of the function.
What are the Steps in Graphing a Linear Function?
The steps to graph a linear function are given as follows:
- Make sure the linear function is of the form y=mx+b.
- Now, b is plotted on the y-axis.
- m is converted into a fraction .
- Now the line is extended from b using the slope .
- The line can further be extended using m as a guiding factor.
Alternatively:
Any two points on a line determine the line . So to graph a linear function, we just need two points on it. To graph it, just construct a table of values with two columns x and y, take some random numbers for x, and calculate the corresponding values of y by substituting each of them in the function. Then just plot the points on a graph, join them by a line, and extend the line on both sides infinitely.
How Do You Graph a Piecewise Function?
A piecewise function is defined in different ways (using different equations) in different intervals. We just have to consider each equation as a different function on the given domain and graph it just like how we graph a normal function. To understand more about graphing a piecewise function, click here .
How to Identify Identify Functions Using Graphs?
Here are a few tricks to identify the functions from graphs:
- If the graph is a line, then it is a linear function and is of the form f(x) = ax + b.
- If the graph is a perfect U or inverted U shaped, then it is a quadratic function and is of the form f(x) = ax 2 + bx + c.
- If the graph has two curves that are symmetric about a slanting line then its a rational function and is of the form f(x) = (ax + b) / (cx + d) usually.
- If the graph is V or inverted V shaped then its an absolute value function and is of the form f(x) = a |bx + c| + d.
- If the graph has multiple horizontal line pieces, then it represents a floor function or ceiling function.
- If a graph with a single curve is increasing or decreasing having a vertical asymptote, then it is a logarithmic function.
- If a graph with a single curve is increasing or decreasing having a horizontal asymptote, then it is an exponential function.
- If the graph has multiple waves, that may be one of the trigonometric functions: Sine function Cosine function Tangent function Cosecant function Secant function Cotangent function
How Do You Know If the Graph is a Function?
A function always passes the vertical line test . To use this test, just take a vertical line (or just a vertical stick) and make it pass through the graph from left to right horizontally. At no point in time, the line shouldn't intersect the graph at more than one point for the graph to represent a function.
How do you Use a Graph to Solve an Equation?
First, identify the type of the function by looking at the graph. Take its general equation. Use some points on the graph and the general equation to determine the exact equation of the function.
How do you Sketch a Graph of an Equation?
To sketch a graph of an equation of a function, do the following:
- Plot various points for the equation .
- Join the points and form the curve. The curve so obtained is a graph of the given equation.
Module 5: Function Basics
Characteristics of functions and their graphs, learning outcomes.
- Determine whether a relation represents a function.
- Find function values.
- Determine whether a function is one-to-one.
- Use the vertical line test to identify functions.
- Graph the functions in the library of functions.
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.

Characteristics of Functions
A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain of the relation and the set of the second components of each ordered pair is called the range of the relation. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice the first.
[latex]\left\{\left(1,2\right),\left(2,4\right),\left(3,6\right),\left(4,8\right),\left(5,10\right)\right\}[/latex]
The domain is [latex]\left\{1,2,3,4,5\right\}[/latex]. The range is [latex]\left\{2,4,6,8,10\right\}[/latex].
Note the values in the domain are also known as an input values, or values of the independent variable , and are often labeled with the lowercase letter [latex]x[/latex]. Values in the range are also known as an output values, or values of the dependent variable , and are often labeled with the lowercase letter [latex]y[/latex].
A function [latex]f[/latex] is a relation that assigns a single value in the range to each value in the domain . In other words, no [latex]x[/latex]-values are used more than once. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, [latex]\left\{1,2,3,4,5\right\}[/latex], is paired with exactly one element in the range, [latex]\left\{2,4,6,8,10\right\}[/latex].
Now let’s consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as
[latex]\left\{\left(\text{odd},1\right),\left(\text{even},2\right),\left(\text{odd},3\right),\left(\text{even},4\right),\left(\text{odd},5\right)\right\}[/latex]
Notice that each element in the domain, [latex]\left\{\text{even,}\text{odd}\right\}[/latex] is not paired with exactly one element in the range, [latex]\left\{1,2,3,4,5\right\}[/latex]. For example, the term “odd” corresponds to three values from the domain, [latex]\left\{1,3,5\right\}[/latex] and the term “even” corresponds to two values from the range, [latex]\left\{2,4\right\}[/latex]. This violates the definition of a function, so this relation is not a function.
This image compares relations that are functions and not functions.
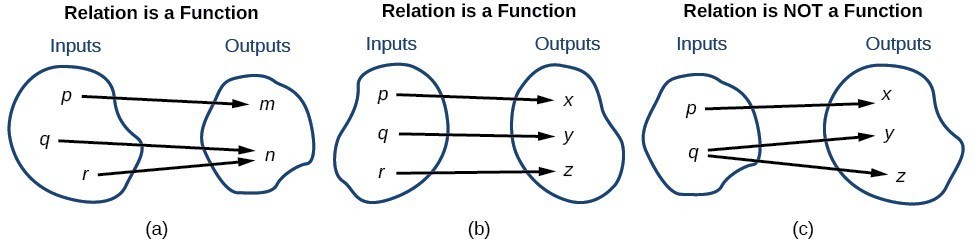
(a) This relationship is a function because each input is associated with a single output. Note that input [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. (b) This relationship is also a function. In this case, each input is associated with a single output. (c) This relationship is not a function because input [latex]q[/latex] is associated with two different outputs.
A General Note: FunctionS
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain , and the output values make up the range .
How To: Given a relationship between two quantities, determine whether the relationship is a function.
- Identify the input values.
- Identify the output values.
- If each input value leads to only one output value, the relationship is a function. If any input value leads to two or more outputs, the relationship is not a function.
Example: Determining If Menu Price Lists Are Functions
The coffee shop menu consists of items and their prices.
- Is price a function of the item?
- Is the item a function of the price?

Example: Determining If Class Grade Rules Are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? The table below shows a possible rule for assigning grade points.
| Percent Grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
|---|---|---|---|---|---|---|---|---|
| Grade Point Average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
For any percent grade earned, there is an associated grade point average, so the grade point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average.
In the grading system given, there is a range of percent grades that correspond to the same grade point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade point average.
The table below lists the five greatest baseball players of all time in order of rank.
| Player | Rank |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- Is the rank a function of the player name?
- Is the player name a function of the rank?
- yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
Using Function Notation
Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into computers. There are various ways of representing functions. A standard function notation is one representation that makes it easier to work with functions.
To represent “height is a function of age,” we start by identifying the descriptive variables [latex]h[/latex] for height and [latex]a[/latex] for age. The letters [latex]f,g[/latex], and [latex]h[/latex] are often used to represent functions just as we use [latex]x,y[/latex], and [latex]z[/latex] to represent numbers and [latex]A,B[/latex], and [latex]C[/latex] to represent sets.
[latex]\begin{align}&h\text{ is }f\text{ of }a &&\text{We name the function }f;\text{ height is a function of age}. \\ &h=f\left(a\right) &&\text{We use parentheses to indicate the function input}\text{. } \\ &f\left(a\right) &&\text{We name the function }f;\text{ the expression is read as }''f\text{ of }a''. \end{align}[/latex]
Remember, we can use any letter to name the function; we can use the notation [latex]h\left(a\right)[/latex] to show that [latex]h[/latex] depends on [latex]a[/latex]. The input value [latex]a[/latex] must be put into the function [latex]h[/latex] to get an output value. The parentheses indicate that age is input into the function; they do not indicate multiplication.
We can also give an algebraic expression as the input to a function. For example [latex]f\left(a+b\right)[/latex] means “first add [latex]a[/latex] and [latex]b[/latex], and the result is the input for the function [latex]f[/latex].” We must perform the operations in this order to obtain the correct result.
A General Note: Function Notation
The notation [latex]y=f\left(x\right)[/latex] defines a function named [latex]f[/latex]. This is read as [latex]``y[/latex] is a function of [latex]x.''[/latex] The letter [latex]x[/latex] represents the input value, or independent variable. The letter [latex]y[/latex], or [latex]f\left(x\right)[/latex], represents the output value, or dependent variable.
Example: Using Function Notation for Days in a Month
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month in a non-leap year.
The number of days in a month is a function of the name of the month, so if we name the function [latex]f[/latex], we write [latex]\text{days}=f\left(\text{month}\right)[/latex] or [latex]d=f\left(m\right)[/latex]. The name of the month is the input to a “rule” that associates a specific number (the output) with each input.
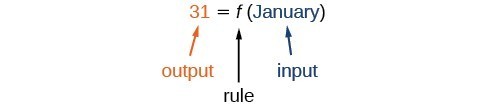
For example, [latex]f\left(\text{April}\right)=30[/latex], because April has 30 days. The notation [latex]d=f\left(m\right)[/latex] reminds us that the number of days, [latex]d[/latex] (the output), is dependent on the name of the month, [latex]m[/latex] (the input).
Analysis of the Solution
We must restrict the function to non-leap years. Otherwise February would have 2 outputs and this would not be a function. Also note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with in this book will have numbers as inputs and outputs.
Example: Interpreting Function Notation
A function [latex]N=f\left(y\right)[/latex] gives the number of police officers, [latex]N[/latex], in a town in year [latex]y[/latex]. What does [latex]f\left(2005\right)=300[/latex] represent?
When we read [latex]f\left(2005\right)=300[/latex], we see that the input year is 2005. The value for the output, the number of police officers [latex]N[/latex], is 300. Remember, [latex]N=f\left(y\right)[/latex]. The statement [latex]f\left(2005\right)=300[/latex] tells us that in the year 2005 there were 300 police officers in the town.
Instead of a notation such as [latex]y=f\left(x\right)[/latex], could we use the same symbol for the output as for the function, such as [latex]y=y\left(x\right)[/latex], meaning “ y is a function of x ?”
Yes, this is often done, especially in applied subjects that use higher math, such as physics and engineering. However, in exploring math itself we like to maintain a distinction between a function such as [latex]f[/latex], which is a rule or procedure, and the output [latex]y[/latex] we get by applying [latex]f[/latex] to a particular input [latex]x[/latex]. This is why we usually use notation such as [latex]y=f\left(x\right),P=W\left(d\right)[/latex], and so on.
Representing Functions Using Tables
A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases these values represent all we know about the relationship; other times the table provides a few select examples from a more complete relationship.
The table below lists the input number of each month (January = 1, February = 2, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year (that is not a leap year). Note that, in this table, we define a days-in-a-month function [latex]f[/latex], where [latex]D=f\left(m\right)[/latex] identifies months by an integer rather than by name.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
The table below defines a function [latex]Q=g\left(n\right)[/latex]. Remember, this notation tells us that [latex]g[/latex] is the name of the function that takes the input [latex]n[/latex] and gives the output [latex]Q[/latex].
| [latex]n[/latex] | 1 | 2 | 3 | 4 | 5 |
| [latex]Q[/latex] | 8 | 6 | 7 | 6 | 8 |
The table below displays the age of children in years and their corresponding heights. This table displays just some of the data available for the heights and ages of children. We can see right away that this table does not represent a function because the same input value, 5 years, has two different output values, 40 in. and 42 in.
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 40 | 42 | 44 | 47 | 50 | 52 | 54 |
How To: Given a table of input and output values, determine whether the table represents a function.
- Identify the input and output values.
- Check to see if each input value is paired with only one output value. If so, the table represents a function.
Example: Identifying Tables that Represent Functions
Which table, A, B, or C, represents a function (if any)?
| Table A | |
|---|---|
| Input | Output |
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Table B | |
|---|---|
| Input | Output |
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Table C | |
|---|---|
| Input | Output |
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
a) and b) define functions. In both, each input value corresponds to exactly one output value. c) does not define a function because the input value of 5 corresponds to two different output values.
When a table represents a function, corresponding input and output values can also be specified using function notation.
The function represented by a) can be represented by writing
[latex]f\left(2\right)=1,f\left(5\right)=3,\text{and }f\left(8\right)=6[/latex]
Similarly, the statements [latex]g\left(-3\right)=5,g\left(0\right)=1,\text{and }g\left(4\right)=5[/latex] represent the function in b).
c) cannot be expressed in a similar way because it does not represent a function.
When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.
When we know an output value and want to determine the input values that would produce that output value, we set the output equal to the function’s formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.
Determine whether a function is one-to-one
Some functions have a given output value that corresponds to two or more input values. For example, in the following stock chart the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000.
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in.
| Letter grade | Grade point average |
|---|---|
| A | 4.0 |
| B | 3.0 |
| C | 2.0 |
| D | 1.0 |
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
To visualize this concept, let’s look again at the two simple functions sketched in (a) and (b) below.
The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.
A General Note: One-to-One Function
A one-to-one function is a function in which each output value corresponds to exactly one input value.
Example: Determining Whether a Relationship Is a One-to-One Function
Is the area of a circle a function of its radius? If yes, is the function one-to-one?
A circle of radius [latex]r[/latex] has a unique area measure given by [latex]A=\pi {r}^{2}[/latex], so for any input, [latex]r[/latex], there is only one output, [latex]A[/latex]. The area is a function of radius [latex]r[/latex].
If the function is one-to-one, the output value, the area, must correspond to a unique input value, the radius. Any area measure [latex]A[/latex] is given by the formula [latex]A=\pi {r}^{2}[/latex]. Because areas and radii are positive numbers, there is exactly one solution: [latex]r=\sqrt{\frac{A}{\pi }}[/latex]. So the area of a circle is a one-to-one function of the circle’s radius.
- Is a balance a function of the bank account number?
- Is a bank account number a function of the balance?
- Is a balance a one-to-one function of the bank account number?
- yes, because each bank account (input) has a single balance (output) at any given time.
- no, because several bank accounts (inputs) may have the same balance (output).
- no, because the more than one bank account (input) can have the same balance (output).
Evaluating and Solving Functions
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function [latex]f\left(x\right)=5 - 3{x}^{2}[/latex] can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.
How To: EVALUATE A FUNCTION Given ITS FORMula.
- Replace the input variable in the formula with the value provided.
- Calculate the result.
Example: Evaluating Functions
Given the function [latex]h\left(p\right)={p}^{2}+2p[/latex], evaluate [latex]h\left(4\right)[/latex].
To evaluate [latex]h\left(4\right)[/latex], we substitute the value 4 for the input variable [latex]p[/latex] in the given function.
[latex]\begin{align}h\left(p\right)&={p}^{2}+2p \\ h\left(4\right)&={\left(4\right)}^{2}+2\left(4\right) \\ &=16+8 \\ &=24 \end{align}[/latex]
Therefore, for an input of 4, we have an output of 24 or [latex]h(4)=24[/latex].
Example: Evaluating Functions at Specific Values
For the function, [latex]f\left(x\right)={x}^{2}+3x - 4[/latex], evaluate each of the following.
- [latex]f\left(2\right)[/latex]
- [latex]f(a)[/latex]
- [latex]f(a+h)[/latex]
- [latex]\dfrac{f\left(a+h\right)-f\left(a\right)}{h}[/latex]
Replace the [latex]x[/latex] in the function with each specified value.
- Because the input value is a number, 2, we can use algebra to simplify. [latex]\begin{align}f\left(2\right)&={2}^{2}+3\left(2\right)-4 \\ &=4+6 - 4 \\ &=6\hfill \end{align}[/latex]
- In this case, the input value is a letter so we cannot simplify the answer any further. [latex]f\left(a\right)={a}^{2}+3a - 4[/latex]
- With an input value of [latex]a+h[/latex], we must use the distributive property. [latex]\begin{align}f\left(a+h\right)&={\left(a+h\right)}^{2}+3\left(a+h\right)-4 \\[2mm] &={a}^{2}+2ah+{h}^{2}+3a+3h - 4 \end{align}[/latex]
and we know that
Now we combine the results and simplify.
[latex]\begin{align}\dfrac{f\left(a+h\right)-f\left(a\right)}{h}&=\dfrac{\left({a}^{2}+2ah+{h}^{2}+3a+3h - 4\right)-\left({a}^{2}+3a - 4\right)}{h} \\[2mm] &=\dfrac{2ah+{h}^{2}+3h}{h}\\[2mm] &=\frac{h\left(2a+h+3\right)}{h}&&\text{Factor out }h. \\[2mm] &=2a+h+3&&\text{Simplify}.\end{align}[/latex]
Given the function [latex]g\left(m\right)=\sqrt{m - 4}[/latex], evaluate [latex]g\left(5\right)[/latex].
[latex]g\left(5\right)=\sqrt{5- 4}=1[/latex]
Example: Solving Functions
Given the function [latex]h\left(p\right)={p}^{2}+2p[/latex], solve for [latex]h\left(p\right)=3[/latex].
[latex]\begin{align}&h\left(p\right)=3\\ &{p}^{2}+2p=3 &&\text{Substitute the original function }h\left(p\right)={p}^{2}+2p. \\ &{p}^{2}+2p - 3=0 &&\text{Subtract 3 from each side}. \\ &\left(p+3\text{)(}p - 1\right)=0 &&\text{Factor}. \end{align}[/latex]
If [latex]\left(p+3\right)\left(p - 1\right)=0[/latex], either [latex]\left(p+3\right)=0[/latex] or [latex]\left(p - 1\right)=0[/latex] (or both of them equal 0). We will set each factor equal to 0 and solve for [latex]p[/latex] in each case.
[latex]\begin{align}&p+3=0, &&p=-3 \\ &p - 1=0, &&p=1\hfill \end{align}[/latex]
This gives us two solutions. The output [latex]h\left(p\right)=3[/latex] when the input is either [latex]p=1[/latex] or [latex]p=-3[/latex].
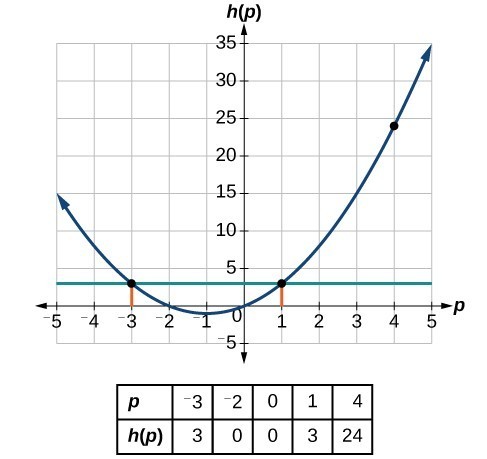
We can also verify by graphing as in Figure 5. The graph verifies that [latex]h\left(1\right)=h\left(-3\right)=3[/latex] and [latex]h\left(4\right)=24[/latex].
Given the function [latex]g\left(m\right)=\sqrt{m - 4}[/latex], solve [latex]g\left(m\right)=2[/latex].
[latex]m=8[/latex]
Evaluating Functions Expressed in Formulas
Some functions are defined by mathematical rules or procedures expressed in equation form. If it is possible to express the function output with a formula involving the input quantity, then we can define a function in algebraic form. For example, the equation [latex]2n+6p=12[/latex] expresses a functional relationship between [latex]n[/latex] and [latex]p[/latex]. We can rewrite it to decide if [latex]p[/latex] is a function of [latex]n[/latex].
How To: Given a function in equation form, write its algebraic formula.
- Solve the equation to isolate the output variable on one side of the equal sign, with the other side as an expression that involves only the input variable.
- Use all the usual algebraic methods for solving equations, such as adding or subtracting the same quantity to or from both sides, or multiplying or dividing both sides of the equation by the same quantity.
Example: Finding an Equation of a Function
Express the relationship [latex]2n+6p=12[/latex] as a function [latex]p=f\left(n\right)[/latex], if possible.
To express the relationship in this form, we need to be able to write the relationship where [latex]p[/latex] is a function of [latex]n[/latex], which means writing it as [latex]p=[/latex] expression involving [latex]n[/latex].
[latex]\begin{align}&2n+6p=12\\[1mm] &6p=12 - 2n &&\text{Subtract }2n\text{ from both sides}. \\[1mm] &p=\frac{12 - 2n}{6} &&\text{Divide both sides by 6 and simplify}. \\[1mm] &p=\frac{12}{6}-\frac{2n}{6} \\[1mm] &p=2-\frac{1}{3}n \end{align}[/latex]
Therefore, [latex]p[/latex] as a function of [latex]n[/latex] is written as
[latex]p=f\left(n\right)=2-\frac{1}{3}n[/latex]
It is important to note that not every relationship expressed by an equation can also be expressed as a function with a formula.
Example: Expressing the Equation of a Circle as a Function
Does the equation [latex]{x}^{2}+{y}^{2}=1[/latex] represent a function with [latex]x[/latex] as input and [latex]y[/latex] as output? If so, express the relationship as a function [latex]y=f\left(x\right)[/latex].
First we subtract [latex]{x}^{2}[/latex] from both sides.
[latex]{y}^{2}=1-{x}^{2}[/latex]
We now try to solve for [latex]y[/latex] in this equation.
[latex]\begin{align}y&=\pm \sqrt{1-{x}^{2}} \\[1mm] &=\sqrt{1-{x}^{2}}\hspace{3mm}\text{and}\hspace{3mm}-\sqrt{1-{x}^{2}} \end{align}[/latex]
We get two outputs corresponding to the same input, so this relationship cannot be represented as a single function [latex]y=f\left(x\right)[/latex].
If [latex]x - 8{y}^{3}=0[/latex], express [latex]y[/latex] as a function of [latex]x[/latex].
Are there relationships expressed by an equation that do represent a function but which still cannot be represented by an algebraic formula?
Yes, this can happen. For example, given the equation [latex]x=y+{2}^{y}[/latex], if we want to express [latex]y[/latex] as a function of [latex]x[/latex], there is no simple algebraic formula involving only [latex]x[/latex] that equals [latex]y[/latex]. However, each [latex]x[/latex] does determine a unique value for [latex]y[/latex], and there are mathematical procedures by which [latex]y[/latex] can be found to any desired accuracy. In this case, we say that the equation gives an implicit (implied) rule for [latex]y[/latex] as a function of [latex]x[/latex], even though the formula cannot be written explicitly.
Evaluating a Function Given in Tabular Form
As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables. For example, how well do our pets recall the fond memories we share with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is just a myth. Goldfish can remember up to 3 months, while the beta fish has a memory of up to 5 months. And while a puppy’s memory span is no longer than 30 seconds, the adult dog can remember for 5 minutes. This is meager compared to a cat, whose memory span lasts for 16 hours.
The function that relates the type of pet to the duration of its memory span is more easily visualized with the use of a table. See the table below.
| Pet | Memory span in hours |
|---|---|
| Puppy | 0.008 |
| Adult dog | 0.083 |
| Cat | 16 |
| Goldfish | 2160 |
| Beta fish | 3600 |
At times, evaluating a function in table form may be more useful than using equations. Here let us call the function [latex]P[/latex].
The domain of the function is the type of pet and the range is a real number representing the number of hours the pet’s memory span lasts. We can evaluate the function [latex]P[/latex] at the input value of “goldfish.” We would write [latex]P\left(\text{goldfish}\right)=2160[/latex]. Notice that, to evaluate the function in table form, we identify the input value and the corresponding output value from the pertinent row of the table. The tabular form for function [latex]P[/latex] seems ideally suited to this function, more so than writing it in paragraph or function form.
How To: Given a function represented by a table, identify specific output and input values.
- Find the given input in the row (or column) of input values.
- Identify the corresponding output value paired with that input value.
- Find the given output values in the row (or column) of output values, noting every time that output value appears.
- Identify the input value(s) corresponding to the given output value.
Example: Evaluating and Solving a Tabular Function
Using the table below,
- Evaluate [latex]g\left(3\right)[/latex].
- Solve [latex]g\left(n\right)=6[/latex].
| 1 | 2 | 3 | 4 | 5 | |
| 8 | 6 | 7 | 6 | 8 |
- Evaluating [latex]g\left(3\right)[/latex] means determining the output value of the function [latex]g[/latex] for the input value of [latex]n=3[/latex]. The table output value corresponding to [latex]n=3[/latex] is 7, so [latex]g\left(3\right)=7[/latex].
- Solving [latex]g\left(n\right)=6[/latex] means identifying the input values, [latex]n[/latex], that produce an output value of 6. The table below shows two solutions: [latex]n=2[/latex] and [latex]n=4[/latex].
When we input 2 into the function [latex]g[/latex], our output is 6. When we input 4 into the function [latex]g[/latex], our output is also 6.
Using the table from the previous example, evaluate [latex]g\left(1\right)[/latex] .
Finding Function Values from a Graph
Evaluating a function using a graph also requires finding the corresponding output value for a given input value, only in this case, we find the output value by looking at the graph. Solving a function equation using a graph requires finding all instances of the given output value on the graph and observing the corresponding input value(s).
Example: Reading Function Values from a Graph
Given the graph below,
- Evaluate [latex]f\left(2\right)[/latex].
- Solve [latex]f\left(x\right)=4[/latex].
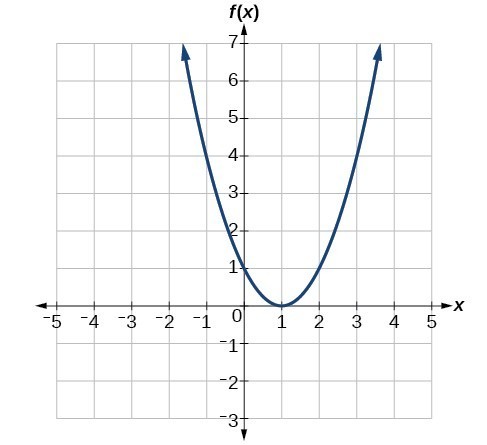
Using the graph, solve [latex]f\left(x\right)=1[/latex].
[latex]x=0[/latex] or [latex]x=2[/latex]
Identify Functions Using Graphs
As we have seen in examples above, we can represent a function using a graph. Graphs display many input-output pairs in a small space. The visual information they provide often makes relationships easier to understand. We typically construct graphs with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value [latex]x[/latex] and the output value [latex]y[/latex], and we say [latex]y[/latex] is a function of [latex]x[/latex], or [latex]y=f\left(x\right)[/latex] when the function is named [latex]f[/latex]. The graph of the function is the set of all points [latex]\left(x,y\right)[/latex] in the plane that satisfies the equation [latex]y=f\left(x\right)[/latex]. If the function is defined for only a few input values, then the graph of the function is only a few points, where the x -coordinate of each point is an input value and the y -coordinate of each point is the corresponding output value. For example, the black dots on the graph in the graph below tell us that [latex]f\left(0\right)=2[/latex] and [latex]f\left(6\right)=1[/latex]. However, the set of all points [latex]\left(x,y\right)[/latex] satisfying [latex]y=f\left(x\right)[/latex] is a curve. The curve shown includes [latex]\left(0,2\right)[/latex] and [latex]\left(6,1\right)[/latex] because the curve passes through those points.
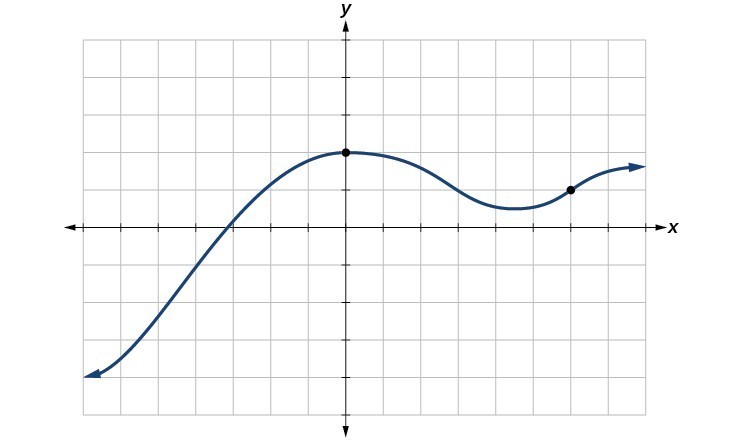
The vertical line test can be used to determine whether a graph represents a function. A vertical line includes all points with a particular [latex]x[/latex] value. The [latex]y[/latex] value of a point where a vertical line intersects a graph represents an output for that input [latex]x[/latex] value. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because that [latex]x[/latex] value has more than one output. A function has only one output value for each input value.
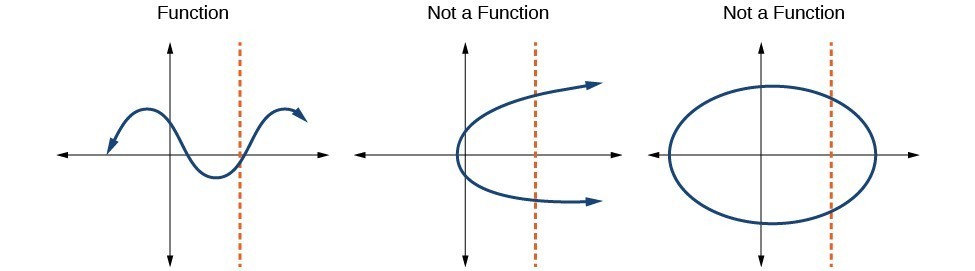
How To: Given a graph, use the vertical line test to determine if the graph represents a function.
- Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
- If there is any such line, the graph does not represent a function.
- If no vertical line can intersect the curve more than once, the graph does represent a function.
Example: Applying the Vertical Line Test
Which of the graphs represent(s) a function [latex]y=f\left(x\right)?[/latex]
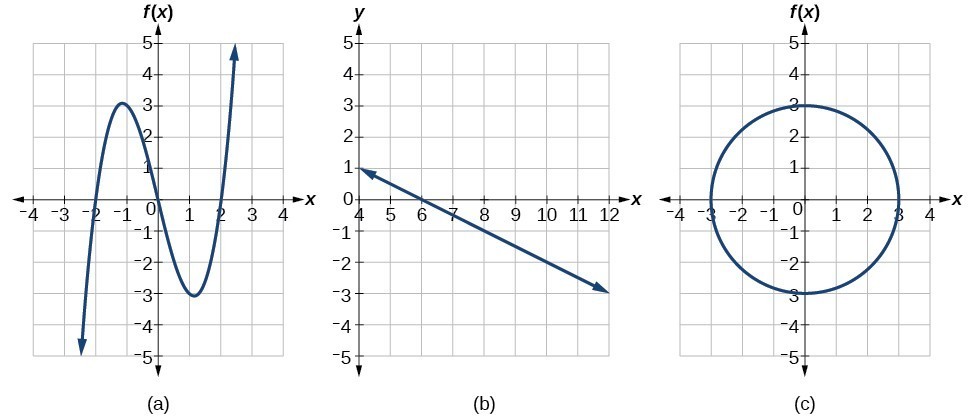
If any vertical line intersects a graph more than once, the relation represented by the graph is not a function. Notice that any vertical line would pass through only one point of the two graphs shown in parts (a) and (b) of the graph above. From this we can conclude that these two graphs represent functions. The third graph does not represent a function because, at most x -values, a vertical line would intersect the graph at more than one point.
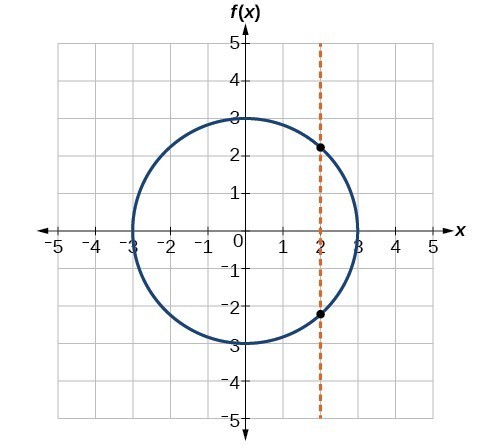
Does the graph below represent a function?
The Horizontal Line Test
Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test . Draw horizontal lines through the graph. A horizontal line includes all points with a particular [latex]y[/latex] value. The [latex]x[/latex] value of a point where a vertical line intersects a function represents the input for that output [latex]y[/latex] value. If we can draw any horizontal line that intersects a graph more than once, then the graph does not represent a one-to-one function because that [latex]y[/latex] value has more than one input.
How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, the function is not one-to-one.
- If no horizontal line can intersect the curve more than once, the function is one-to-one.
Example: Applying the Horizontal Line Test
Consider the functions (a), and (b)shown in the graphs below.
Are either of the functions one-to-one?
The function in (a) is not one-to-one. The horizontal line shown below intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)
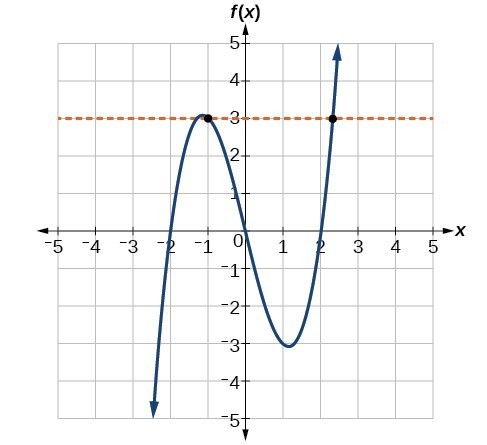
The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
Identifying Basic Toolkit Functions
In this text, we explore functions—the shapes of their graphs, their unique characteristics, their algebraic formulas, and how to solve problems with them. When learning to read, we start with the alphabet. When learning to do arithmetic, we start with numbers. When working with functions, it is similarly helpful to have a base set of building-block elements. We call these our “toolkit functions,” which form a set of basic named functions for which we know the graph, formula, and special properties. Some of these functions are programmed to individual buttons on many calculators. For these definitions we will use [latex]x[/latex] as the input variable and [latex]y=f\left(x\right)[/latex] as the output variable.
We will see these toolkit functions, combinations of toolkit functions, their graphs, and their transformations frequently throughout this book. It will be very helpful if we can recognize these toolkit functions and their features quickly by name, formula, graph, and basic table properties. The graphs and sample table values are included with each function shown below.
| Toolkit Functions | ||
|---|---|---|
| Name | Function | Graph |
| Constant | [latex]f\left(x\right)=c[/latex], where [latex]c[/latex] is a constant | |
| Identity | [latex]f\left(x\right)=x[/latex] | |
| Absolute value | [latex]f\left(x\right)=|x|[/latex] | |
| Quadratic | [latex]f\left(x\right)={x}^{2}[/latex] | |
| Cubic | [latex]f\left(x\right)={x}^{3}[/latex] | |
| Reciprocal/ Rational | [latex]f\left(x\right)=\frac{1}{x}[/latex] | |
| Reciprocal / Rational squared | [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex] | |
| Square root | [latex]f\left(x\right)=\sqrt{x}[/latex] | |
| Cube root | [latex]f\left(x\right)=\sqrt[3]{x}[/latex] | |
Key Concepts
- A relation is a set of ordered pairs. A function is a specific type of relation in which each domain value, or input, leads to exactly one range value, or output.
- Function notation is a shorthand method for relating the input to the output in the form [latex]y=f\left(x\right)[/latex].
- In table form, a function can be represented by rows or columns that relate to input and output values.
- To evaluate a function we determine an output value for a corresponding input value. Algebraic forms of a function can be evaluated by replacing the input variable with a given value.
- To solve for a specific function value, we determine the input values that yield the specific output value.
- An algebraic form of a function can be written from an equation.
- Input and output values of a function can be identified from a table.
- Relating input values to output values on a graph is another way to evaluate a function.
- A function is one-to-one if each output value corresponds to only one input value.
- A graph represents a function if any vertical line drawn on the graph intersects the graph at no more than one point.
- A graph represents a one-to-one function if any horizontal line drawn on the graph intersects the graph at no more than one point.
- Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
- Question ID 111625, 111715, 11722. Provided by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- Question ID 111699. Provided by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Function Notation Application. Authored by : James Sousa. Located at : https://www.youtube.com/watch?v=nAF_GZFwU1g . License : CC BY: Attribution
- Question ID 2510, 1729. Authored by : Lippman, David. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- Question ID 15800. Authored by : James Sousa (Mathispower4u.com). License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- Question ID 1647. Authored by : WebWork-Rochester, mb Lippman,David, mb Sousa,James. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- Question ID 97486. Authored by : Carmichael, Patrick. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- Question ID 15766, 2886, 3751. Authored by : Lippman, David. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- Question ID 40676. Authored by : Micheal Jenck. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- Determine if a Relation is a Function. Authored by : James Sousa. Located at : https://youtu.be/zT69oxcMhPw . License : All Rights Reserved . License Terms : Standard YouTube License
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.
- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| ▭\:\longdivision{▭} | \times \twostack{▭}{▭} | + \twostack{▭}{▭} | - \twostack{▭}{▭} | \left( | \right) | \times | \square\frac{\square}{\square} |
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- Pre Calculus
- Given Points
- Given Slope & Point
- Slope Intercept Form
- Start Point
- Parallel Lines
- Perpendicular
- Perpendicular Lines
- Perpendicular Slope
- Is a Function
- Domain & Range
- Slope & Intercepts
- Periodicity
- Domain of Inverse
- Critical Points
- Inflection Points
- Monotone Intervals
- Extreme Points
- Global Extreme Points
- Absolute Extreme
- Turning Points
- End Behavior
- Average Rate of Change
- Piecewise Functions
- Discontinuity
- Values Table
- Function Reciprocal
- Function Negative Reciprocal
- Compositions
- Arithmetics
- Circumference
- Eccentricity
- Conic Inequalities
- Transformation
- Linear Algebra
- Trigonometry
- Conversions
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| - \twostack{▭}{▭} | \lt | 7 | 8 | 9 | \div | AC |
| + \twostack{▭}{▭} | \gt | 4 | 5 | 6 | \times | \square\frac{\square}{\square} |
| \times \twostack{▭}{▭} | \left( | 1 | 2 | 3 | - | x |
| ▭\:\longdivision{▭} | \right) | . | 0 | = | + | y |
Number Line
- y=\frac{x^2+x+1}{x}
- f(x)=\ln (x-5)
- f(x)=\frac{1}{x^2}
- y=\frac{x}{x^2-6x+8}
- f(x)=\sqrt{x+3}
- f(x)=\cos(2x+5)
- f(x)=\sin(3x)
| 🌐 Languages | EN, ES, PT & more |
|---|---|
| 🏆 Practice | Improve your math skills |
| 😍 Step by step | In depth solution steps |
| ⭐️ Rating | based on 20924 reviews |
functions-calculator
- Functions A function basically relates an input to an output, there’s an input, a relationship and an output. For every input...
We want your feedback
Please add a message.
Message received. Thanks for the feedback.

IMAGES
VIDEO
COMMENTS
Graphing Calculator
ID: 5 Name_____ Assignment Date_____ Period____ Sketch the graph of each function. 1) y x x 2) y x x 3) y x x 4) y x x math-worksheet.org
Graphing Polynomial Functions Date_____ Period____ State the maximum number of turns the graph of each function could make. Then sketch the graph. State the number of real zeros. Approximate each zero to the nearest tenth. Approximate the relative minima and relative maxima to the nearest tenth. 1) f (
Here we will learn about sketching quadratic graphs including how to identify key points on a graph of a quadratic function, and how to sketch quadratic graphs from these key ... This vertex is a minimum, because we're dealing with a u shaped graph. Sketch a set of axes, label each of the key points, then join with a smooth curve: Example 2 ...
10) Write a rule for the function shown. f (x) x x , x x , x . Create your own worksheets like this one with Infinite Precalculus. Free trial available at KutaSoftware.com.
To sketch the graph of a function, we need to perform the following: Determine, whether function is obtained by transforming a simpler function, and perform necessary steps for this simpler function. Determine, whether function is even, odd or periodic. This allows to draw graph of the function on some subinterval and then just reflect the ...
Given a function f f use the following steps to sketch a graph of f f: Determine the domain of the function. Locate the x x - and y y -intercepts. Evaluate lim x→∞f (x) lim x → ∞ f (x) and lim x→−∞f (x) lim x → − ∞ f (x) to determine the end behavior. If either of these limits is a finite number L L, then y = L y = L is a ...
©L a2S0d1 w2c UKQu8tDa X 5Sdoufxt Aw7aDrqed lL qL mCl. N 6 uAOljl 4 4r eiug ehXtWs9 YrNeqsXe3r TvRezd m.s 5 2M maSdje T Jwpijtrhq sI mnZfIi ZnAi6t veT MA4l hgje Ybreag E1e.e Worksheet by Kuta Software LLC
When I begin to sketch the graph of a function, I first consider its domain and range. The domain represents all possible input values (usually the x -values), which are the real numbers that can be plugged into the function without causing any undefined behavior. For example, in the function f (x) = 2 x − 1, the domain excludes the value x ...
A third representation of the function f is the graph of the ordered pairs of the function, shown in the Cartesian plane in Figure \(\PageIndex{3}\)(b). Figure \(\PageIndex{3}\) A mapping diagram and its graph. When the function is represented by an equation or formula, then we adjust our definition of its graph somewhat.
Key Idea 4: Curve Sketching. To produce an accurate sketch a given function \(f\), consider the following steps. Find the domain of \(f\). Generally, we assume that the domain is the entire real line then find restrictions, such as where a denominator is 0 or where negatives appear under the radical.
a) The graph shows exponential growth. b) The graph shows exponential decay. c) The graph shows y= (1/2)^x reflected over the x-axis. d) The graph shows y = 2x reflected over the y-axis. How does the graph of y = 3x compare to the graph of y = 3-x? The graphs are the same. The graphs are reflected across the x-axis.
Absolute value-. Translated 12 units up Translated 23 units left. 11. Reciprocal Function. Expanded vertically by a factor of 4 Reflected in the x-axis and translated 2 units up. 12. Greatest Integer Function. Reflected in the y -axis and translated 16 units up. Use the graph of parent function to graph each function.
Write an equation for each graph. 4) x y-4-22468-2 2 4 6 8 10 12 14 16 18 5) x y-8-6-4-2246 2 4 6 8 10 12 14 16 18 20 Graph each number in the complex plane. 6) 4 - i Real Imaginary Identify the vertex of each. Then sketch the graph. 7) y = x2 + 2 x y-8-6-4-22468-8-6-4-2 2 4 6 8 8) y = 2 (x - 2) 2 - 3 x y-8-6-4-22468-8-6-4-2 2 4 6 8
For the following exercises, for each polynomial, a. find the degree; b. find the zeros, if any; c. find the y -intercept (s), if any; d. use the leading coefficient to determine the graph's end behavior; and e. determine algebraically whether the polynomial is even, odd, or neither. 1) f(x) = 2x2 − 3x − 5.
©W 42 Y01Z20 2K Guht XaP uS Ho efJtSwbaFrmeI 4L dL 8Cb. w U RApl Olm sr miTgeh KtIs O yrhe 7swelr YvRejdC. 3 0 bMuaXdIei dwIi kt5hX yIon kfPiLn vi3t Ae7 5A ylng 9eBb VrjaC i1 D.K Worksheet by Kuta Software LLC
Graphing Functions - How to Graph Functions?
Graph the functions in the library of functions. A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions.
The shape of f (x) = √ x , but shifted nine units down and then reflected in both the x-axis and the y-axis f (x) =− √ − x + 9 58. using the graph of f (x) = √ x to write an equation for each function whose graph is shown A. f (x) = 16 √ x B. f (x) = − 1 2 √ x 62. Parent function: y = x Horizontally stretched by ½ Function: y ...
Sketch a graph of this new function. Figure \(\PageIndex{1e}\): V(t) ... then \(g(x)=(x−2)^2\) is a new function. Each input is reduced by 2 prior to squaring the function. The result is that the graph is shifted 2 units to the right, because we would need to increase the prior input by 2 units to yield the same output value as given in \(f ...
Sketch the general shape of each function. 11) f ... State the maximum number of turns the graph of each function could make. 9) f (x) = x5 − 4x3 + 5x + 1 Max # Turns: 4
Mathematics document from Crescent Heights High School, 14 pages, Review Assignment RADICAL AND RATIONAL FUNCTIONS NamEC:—— Teacher: =_———— Total Yo 112 Page 1 of 14 1. Sketeh the graph of the following functions. State the domain and range. / 3 Y =203 > ¢ < 2] Domsins_3 X1 > =38 1 mark : ragee_ 21y penrs 20 n? — 2. Id
Mathematics document from Lester B. Pearson Senior High School, 2 pages, . S Analyzing Radical and Rational Functions Lesson #2: Radical Functions Part Two 451 Assignment The graph of a function y = f{(x) is shown. a) Sketch the graph of y = \/f{x) on the grid. b) State the domain of :"1 fl—'fi' o i) y=Ax) i) y=1Ax c) -* 1. Stat
Functions Calculator