descriptive research hypothesis testing

• How it works

"Christmas Offer"

Terms & conditions.

As the Christmas season is upon us, we find ourselves reflecting on the past year and those who we have helped to shape their future. It’s been quite a year for us all! The end of the year brings no greater joy than the opportunity to express to you Christmas greetings and good wishes.

At this special time of year, Research Prospect brings joyful discount of 10% on all its services. May your Christmas and New Year be filled with joy.

We are looking back with appreciation for your loyalty and looking forward to moving into the New Year together.

"Claim this offer"

In unfamiliar and hard times, we have stuck by you. This Christmas, Research Prospect brings you all the joy with exciting discount of 10% on all its services.

Offer valid till 5-1-2024

We love being your partner in success. We know you have been working hard lately, take a break this holiday season to spend time with your loved ones while we make sure you succeed in your academics

Discount code: RP0996Y

Hypothesis Testing – A Complete Guide with Examples

Published by Alvin Nicolas at August 14th, 2021 , Revised On October 26, 2023

In statistics, hypothesis testing is a critical tool. It allows us to make informed decisions about populations based on sample data. Whether you are a researcher trying to prove a scientific point, a marketer analysing A/B test results, or a manufacturer ensuring quality control, hypothesis testing plays a pivotal role. This guide aims to introduce you to the concept and walk you through real-world examples.

What is a Hypothesis and a Hypothesis Testing?

A hypothesis is considered a belief or assumption that has to be accepted, rejected, proved or disproved. In contrast, a research hypothesis is a research question for a researcher that has to be proven correct or incorrect through investigation.

What is Hypothesis Testing?

Hypothesis testing  is a scientific method used for making a decision and drawing conclusions by using a statistical approach. It is used to suggest new ideas by testing theories to know whether or not the sample data supports research. A research hypothesis is a predictive statement that has to be tested using scientific methods that join an independent variable to a dependent variable.  

Example: The academic performance of student A is better than student B

Characteristics of the Hypothesis to be Tested

A hypothesis should be:

• Clear and precise
• Capable of being tested
• Able to relate to a variable
• Stated in simple terms
• Consistent with known facts
• Limited in scope and specific
• Tested in a limited timeframe
• Explain the facts in detail

What is a Null Hypothesis and Alternative Hypothesis?

A  null hypothesis  is a hypothesis when there is no significant relationship between the dependent and the participants’ independent  variables . 

In simple words, it’s a hypothesis that has been put forth but hasn’t been proved as yet. A researcher aims to disprove the theory. The abbreviation “Ho” is used to denote a null hypothesis.

If you want to compare two methods and assume that both methods are equally good, this assumption is considered the null hypothesis.

Example: In an automobile trial, you feel that the new vehicle’s mileage is similar to the previous model of the car, on average. You can write it as: Ho: there is no difference between the mileage of both vehicles. If your findings don’t support your hypothesis and you get opposite results, this outcome will be considered an alternative hypothesis.

If you assume that one method is better than another method, then it’s considered an alternative hypothesis. The alternative hypothesis is the theory that a researcher seeks to prove and is typically denoted by H1 or HA.

If you support a null hypothesis, it means you’re not supporting the alternative hypothesis. Similarly, if you reject a null hypothesis, it means you are recommending the alternative hypothesis.

Example: In an automobile trial, you feel that the new vehicle’s mileage is better than the previous model of the vehicle. You can write it as; Ha: the two vehicles have different mileage. On average/ the fuel consumption of the new vehicle model is better than the previous model.

If a null hypothesis is rejected during the hypothesis test, even if it’s true, then it is considered as a type-I error. On the other hand, if you don’t dismiss a hypothesis, even if it’s false because you could not identify its falseness, it’s considered a type-II error.

Hire an Expert Researcher

Orders completed by our expert writers are

• Formally drafted in academic style
• 100% Plagiarism free & 100% Confidential
• Never resold
• Include unlimited free revisions
• Completed to match exact client requirements

How to Conduct Hypothesis Testing?

Here is a step-by-step guide on how to conduct hypothesis testing.

Step 1: State the Null and Alternative Hypothesis

Once you develop a research hypothesis, it’s important to state it is as a Null hypothesis (Ho) and an Alternative hypothesis (Ha) to test it statistically.

A null hypothesis is a preferred choice as it provides the opportunity to test the theory. In contrast, you can accept the alternative hypothesis when the null hypothesis has been rejected.

Example: You want to identify a relationship between obesity of men and women and the modern living style. You develop a hypothesis that women, on average, gain weight quickly compared to men. Then you write it as: Ho: Women, on average, don’t gain weight quickly compared to men. Ha: Women, on average, gain weight quickly compared to men.

Step 2: Data Collection

Hypothesis testing follows the statistical method, and statistics are all about data. It’s challenging to gather complete information about a specific population you want to study. You need to  gather the data  obtained through a large number of samples from a specific population. 

Example: Suppose you want to test the difference in the rate of obesity between men and women. You should include an equal number of men and women in your sample. Then investigate various aspects such as their lifestyle, eating patterns and profession, and any other variables that may influence average weight. You should also determine your study’s scope, whether it applies to a specific group of population or worldwide population. You can use available information from various places, countries, and regions.

Step 3: Select Appropriate Statistical Test

There are many  types of statistical tests , but we discuss the most two common types below, such as One-sided and two-sided tests.

Note: Your choice of the type of test depends on the purpose of your study 

One-sided Test

In the one-sided test, the values of rejecting a null hypothesis are located in one tail of the probability distribution. The set of values is less or higher than the critical value of the test. It is also called a one-tailed test of significance.

Example: If you want to test that all mangoes in a basket are ripe. You can write it as: Ho: All mangoes in the basket, on average, are ripe. If you find all ripe mangoes in the basket, the null hypothesis you developed will be true.

Two-sided Test

In the two-sided test, the values of rejecting a null hypothesis are located on both tails of the probability distribution. The set of values is less or higher than the first critical value of the test and higher than the second critical value test. It is also called a two-tailed test of significance. 

Example: Nothing can be explicitly said whether all mangoes are ripe in the basket. If you reject the null hypothesis (Ho: All mangoes in the basket, on average, are ripe), then it means all mangoes in the basket are not likely to be ripe. A few mangoes could be raw as well.

Get statistical analysis help at an affordable price

• An expert statistician will complete your work
• Rigorous quality checks
• Confidentiality and reliability
• Any statistical software of your choice
• Free Plagiarism Report

Step 4: Select the Level of Significance

When you reject a null hypothesis, even if it’s true during a statistical hypothesis, it is considered the  significance level . It is the probability of a type one error. The significance should be as minimum as possible to avoid the type-I error, which is considered severe and should be avoided. 

If the significance level is minimum, then it prevents the researchers from false claims. 

The significance level is denoted by  P,  and it has given the value of 0.05 (P=0.05)

If the P-Value is less than 0.05, then the difference will be significant. If the P-value is higher than 0.05, then the difference is non-significant.

Example: Suppose you apply a one-sided test to test whether women gain weight quickly compared to men. You get to know about the average weight between men and women and the factors promoting weight gain.

Step 5: Find out Whether the Null Hypothesis is Rejected or Supported

After conducting a statistical test, you should identify whether your null hypothesis is rejected or accepted based on the test results. It would help if you observed the P-value for this.

Example: If you find the P-value of your test is less than 0.5/5%, then you need to reject your null hypothesis (Ho: Women, on average, don’t gain weight quickly compared to men). On the other hand, if a null hypothesis is rejected, then it means the alternative hypothesis might be true (Ha: Women, on average, gain weight quickly compared to men. If you find your test’s P-value is above 0.5/5%, then it means your null hypothesis is true.

Step 6: Present the Outcomes of your Study

The final step is to present the  outcomes of your study . You need to ensure whether you have met the objectives of your research or not. 

In the discussion section and  conclusion , you can present your findings by using supporting evidence and conclude whether your null hypothesis was rejected or supported.

In the result section, you can summarise your study’s outcomes, including the average difference and P-value of the two groups.

If we talk about the findings, our study your results will be as follows:

Example: In the study of identifying whether women gain weight quickly compared to men, we found the P-value is less than 0.5. Hence, we can reject the null hypothesis (Ho: Women, on average, don’t gain weight quickly than men) and conclude that women may likely gain weight quickly than men.

Did you know in your academic paper you should not mention whether you have accepted or rejected the null hypothesis? 

Always remember that you either conclude to reject Ho in favor of Haor   do not reject Ho . It would help if you never rejected  Ha  or even  accept Ha .

Suppose your null hypothesis is rejected in the hypothesis testing. If you conclude  reject Ho in favor of Haor   do not reject Ho,  then it doesn’t mean that the null hypothesis is true. It only means that there is a lack of evidence against Ho in favour of Ha. If your null hypothesis is not true, then the alternative hypothesis is likely to be true.

Example: We found that the P-value is less than 0.5. Hence, we can conclude reject Ho in favour of Ha (Ho: Women, on average, don’t gain weight quickly than men) reject Ho in favour of Ha. However, rejected in favour of Ha means (Ha: women may likely to gain weight quickly than men)

Frequently Asked Questions

What are the 3 types of hypothesis test.

The 3 types of hypothesis tests are:

• One-Sample Test : Compare sample data to a known population value.
• Two-Sample Test : Compare means between two sample groups.
• ANOVA : Analyze variance among multiple groups to determine significant differences.

What is a hypothesis?

A hypothesis is a proposed explanation or prediction about a phenomenon, often based on observations. It serves as a starting point for research or experimentation, providing a testable statement that can either be supported or refuted through data and analysis. In essence, it’s an educated guess that drives scientific inquiry.

What are null hypothesis?

A null hypothesis (often denoted as H0) suggests that there is no effect or difference in a study or experiment. It represents a default position or status quo. Statistical tests evaluate data to determine if there’s enough evidence to reject this null hypothesis.

What is the probability value?

The probability value, or p-value, is a measure used in statistics to determine the significance of an observed effect. It indicates the probability of obtaining the observed results, or more extreme, if the null hypothesis were true. A small p-value (typically <0.05) suggests evidence against the null hypothesis, warranting its rejection.

What is p value?

The p-value is a fundamental concept in statistical hypothesis testing. It represents the probability of observing a test statistic as extreme, or more so, than the one calculated from sample data, assuming the null hypothesis is true. A low p-value suggests evidence against the null, possibly justifying its rejection.

What is a t test?

A t-test is a statistical test used to compare the means of two groups. It determines if observed differences between the groups are statistically significant or if they likely occurred by chance. Commonly applied in research, there are different t-tests, including independent, paired, and one-sample, tailored to various data scenarios.

When to reject null hypothesis?

Reject the null hypothesis when the test statistic falls into a predefined rejection region or when the p-value is less than the chosen significance level (commonly 0.05). This suggests that the observed data is unlikely under the null hypothesis, indicating evidence for the alternative hypothesis. Always consider the study’s context.

You May Also Like

In historical research, a researcher collects and analyse the data, and explain the events that occurred in the past to test the truthfulness of observations.

Textual analysis is the method of analysing and understanding the text. We need to look carefully at the text to identify the writer’s context and message.

A confounding variable can potentially affect both the suspected cause and the suspected effect. Here is all you need to know about accounting for confounding variables in research.

As Featured On

USEFUL LINKS

LEARNING RESOURCES

COMPANY DETAILS

Splash Sol LLC

• How It Works

Ohio State nav bar

The Ohio State University

• BuckeyeLink
• Find People
• Search Ohio State

Research Questions & Hypotheses

Generally, in quantitative studies, reviewers expect hypotheses rather than research questions. However, both research questions and hypotheses serve different purposes and can be beneficial when used together.

Research Questions

Clarify the research’s aim (farrugia et al., 2010).

• Research often begins with an interest in a topic, but a deep understanding of the subject is crucial to formulate an appropriate research question.
• Descriptive: “What factors most influence the academic achievement of senior high school students?”
• Comparative: “What is the performance difference between teaching methods A and B?”
• Relationship-based: “What is the relationship between self-efficacy and academic achievement?”
• Increasing knowledge about a subject can be achieved through systematic literature reviews, in-depth interviews with patients (and proxies), focus groups, and consultations with field experts.
• Some funding bodies, like the Canadian Institute for Health Research, recommend conducting a systematic review or a pilot study before seeking grants for full trials.
• The presence of multiple research questions in a study can complicate the design, statistical analysis, and feasibility.
• It’s advisable to focus on a single primary research question for the study.
• The primary question, clearly stated at the end of a grant proposal’s introduction, usually specifies the study population, intervention, and other relevant factors.
• The FINER criteria underscore aspects that can enhance the chances of a successful research project, including specifying the population of interest, aligning with scientific and public interest, clinical relevance, and contribution to the field, while complying with ethical and national research standards.
• The P ICOT approach is crucial in developing the study’s framework and protocol, influencing inclusion and exclusion criteria and identifying patient groups for inclusion.
• Defining the specific population, intervention, comparator, and outcome helps in selecting the right outcome measurement tool.
• The more precise the population definition and stricter the inclusion and exclusion criteria, the more significant the impact on the interpretation, applicability, and generalizability of the research findings.
• A restricted study population enhances internal validity but may limit the study’s external validity and generalizability to clinical practice.
• A broadly defined study population may better reflect clinical practice but could increase bias and reduce internal validity.
• An inadequately formulated research question can negatively impact study design, potentially leading to ineffective outcomes and affecting publication prospects.

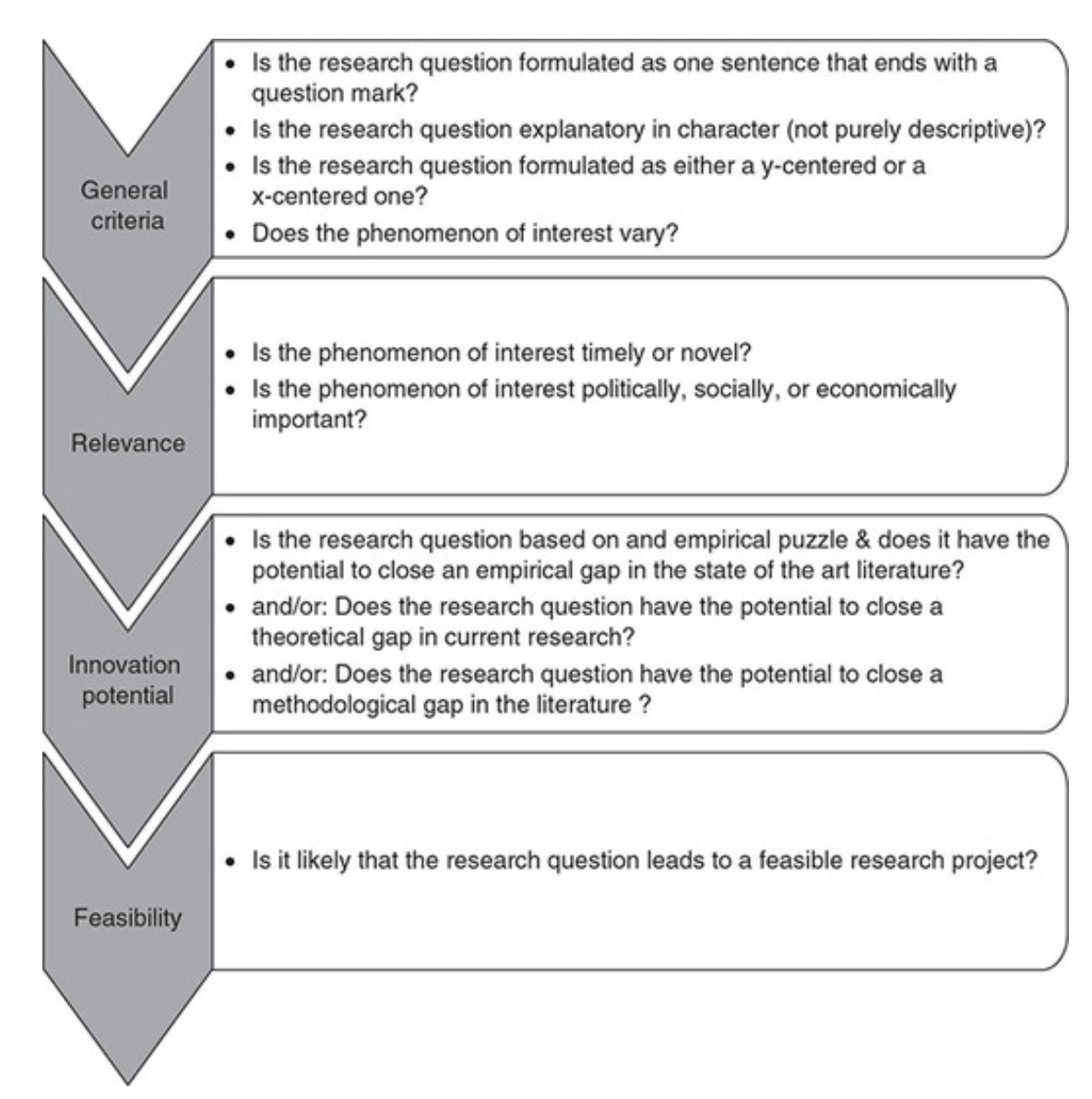
Checklist: Good research questions for social science projects (Panke, 2018)

Research Hypotheses

Present the researcher’s predictions based on specific statements.

• These statements define the research problem or issue and indicate the direction of the researcher’s predictions.
• Formulating the research question and hypothesis from existing data (e.g., a database) can lead to multiple statistical comparisons and potentially spurious findings due to chance.
• The research or clinical hypothesis, derived from the research question, shapes the study’s key elements: sampling strategy, intervention, comparison, and outcome variables.
• Hypotheses can express a single outcome or multiple outcomes.
• After statistical testing, the null hypothesis is either rejected or not rejected based on whether the study’s findings are statistically significant.
• Hypothesis testing helps determine if observed findings are due to true differences and not chance.
• Hypotheses can be 1-sided (specific direction of difference) or 2-sided (presence of a difference without specifying direction).
• 2-sided hypotheses are generally preferred unless there’s a strong justification for a 1-sided hypothesis.
• A solid research hypothesis, informed by a good research question, influences the research design and paves the way for defining clear research objectives.

Types of Research Hypothesis

• In a Y-centered research design, the focus is on the dependent variable (DV) which is specified in the research question. Theories are then used to identify independent variables (IV) and explain their causal relationship with the DV.
• Example: “An increase in teacher-led instructional time (IV) is likely to improve student reading comprehension scores (DV), because extensive guided practice under expert supervision enhances learning retention and skill mastery.”
• Hypothesis Explanation: The dependent variable (student reading comprehension scores) is the focus, and the hypothesis explores how changes in the independent variable (teacher-led instructional time) affect it.
• In X-centered research designs, the independent variable is specified in the research question. Theories are used to determine potential dependent variables and the causal mechanisms at play.
• Example: “Implementing technology-based learning tools (IV) is likely to enhance student engagement in the classroom (DV), because interactive and multimedia content increases student interest and participation.”
• Hypothesis Explanation: The independent variable (technology-based learning tools) is the focus, with the hypothesis exploring its impact on a potential dependent variable (student engagement).
• Probabilistic hypotheses suggest that changes in the independent variable are likely to lead to changes in the dependent variable in a predictable manner, but not with absolute certainty.
• Example: “The more teachers engage in professional development programs (IV), the more their teaching effectiveness (DV) is likely to improve, because continuous training updates pedagogical skills and knowledge.”
• Hypothesis Explanation: This hypothesis implies a probable relationship between the extent of professional development (IV) and teaching effectiveness (DV).
• Deterministic hypotheses state that a specific change in the independent variable will lead to a specific change in the dependent variable, implying a more direct and certain relationship.
• Example: “If the school curriculum changes from traditional lecture-based methods to project-based learning (IV), then student collaboration skills (DV) are expected to improve because project-based learning inherently requires teamwork and peer interaction.”
• Hypothesis Explanation: This hypothesis presumes a direct and definite outcome (improvement in collaboration skills) resulting from a specific change in the teaching method.
• Example : “Students who identify as visual learners will score higher on tests that are presented in a visually rich format compared to tests presented in a text-only format.”
• Explanation : This hypothesis aims to describe the potential difference in test scores between visual learners taking visually rich tests and text-only tests, without implying a direct cause-and-effect relationship.
• Example : “Teaching method A will improve student performance more than method B.”
• Explanation : This hypothesis compares the effectiveness of two different teaching methods, suggesting that one will lead to better student performance than the other. It implies a direct comparison but does not necessarily establish a causal mechanism.
• Example : “Students with higher self-efficacy will show higher levels of academic achievement.”
• Explanation : This hypothesis predicts a relationship between the variable of self-efficacy and academic achievement. Unlike a causal hypothesis, it does not necessarily suggest that one variable causes changes in the other, but rather that they are related in some way.

Tips for developing research questions and hypotheses for research studies

• Perform a systematic literature review (if one has not been done) to increase knowledge and familiarity with the topic and to assist with research development.
• Learn about current trends and technological advances on the topic.
• Seek careful input from experts, mentors, colleagues, and collaborators to refine your research question as this will aid in developing the research question and guide the research study.
• Use the FINER criteria in the development of the research question.
• Ensure that the research question follows PICOT format.
• Develop a research hypothesis from the research question.
• Ensure that the research question and objectives are answerable, feasible, and clinically relevant.

If your research hypotheses are derived from your research questions, particularly when multiple hypotheses address a single question, it’s recommended to use both research questions and hypotheses. However, if this isn’t the case, using hypotheses over research questions is advised. It’s important to note these are general guidelines, not strict rules. If you opt not to use hypotheses, consult with your supervisor for the best approach.

Farrugia, P., Petrisor, B. A., Farrokhyar, F., & Bhandari, M. (2010). Practical tips for surgical research: Research questions, hypotheses and objectives.  Canadian journal of surgery. Journal canadien de chirurgie ,  53 (4), 278–281.

Hulley, S. B., Cummings, S. R., Browner, W. S., Grady, D., & Newman, T. B. (2007). Designing clinical research. Philadelphia.

Panke, D. (2018). Research design & method selection: Making good choices in the social sciences.  Research Design & Method Selection , 1-368.

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

• Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

• Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
• Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
• Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
• Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
• Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.

Recent Activity

• Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.8: Descriptive Research

• Last updated
• Save as PDF
• Page ID 59848

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Differentiate between descriptive, experimental, and correlational research
• Explain the strengths and weaknesses of case studies, naturalistic observation, and surveys

There are many research methods available to psychologists in their efforts to understand, describe, and explain behavior and the cognitive and biological processes that underlie it. Some methods rely on observational techniques. Other approaches involve interactions between the researcher and the individuals who are being studied—ranging from a series of simple questions to extensive, in-depth interviews—to well-controlled experiments.

The three main categories of psychological research are descriptive, correlational, and experimental research. Research studies that do not test specific relationships between variables are called descriptive, or qualitative, studies . These studies are used to describe general or specific behaviors and attributes that are observed and measured. In the early stages of research it might be difficult to form a hypothesis, especially when there is not any existing literature in the area. In these situations designing an experiment would be premature, as the question of interest is not yet clearly defined as a hypothesis. Often a researcher will begin with a non-experimental approach, such as a descriptive study, to gather more information about the topic before designing an experiment or correlational study to address a specific hypothesis. Descriptive research is distinct from correlational research , in which psychologists formally test whether a relationship exists between two or more variables. Experimental research goes a step further beyond descriptive and correlational research and randomly assigns people to different conditions, using hypothesis testing to make inferences about how these conditions affect behavior. It aims to determine if one variable directly impacts and causes another. Correlational and experimental research both typically use hypothesis testing, whereas descriptive research does not.

Each of these research methods has unique strengths and weaknesses, and each method may only be appropriate for certain types of research questions. For example, studies that rely primarily on observation produce incredible amounts of information, but the ability to apply this information to the larger population is somewhat limited because of small sample sizes. Survey research, on the other hand, allows researchers to easily collect data from relatively large samples. While this allows for results to be generalized to the larger population more easily, the information that can be collected on any given survey is somewhat limited and subject to problems associated with any type of self-reported data. Some researchers conduct archival research by using existing records. While this can be a fairly inexpensive way to collect data that can provide insight into a number of research questions, researchers using this approach have no control on how or what kind of data was collected.

Correlational research can find a relationship between two variables, but the only way a researcher can claim that the relationship between the variables is cause and effect is to perform an experiment. In experimental research, which will be discussed later in the text, there is a tremendous amount of control over variables of interest. While this is a powerful approach, experiments are often conducted in very artificial settings. This calls into question the validity of experimental findings with regard to how they would apply in real-world settings. In addition, many of the questions that psychologists would like to answer cannot be pursued through experimental research because of ethical concerns.

The three main types of descriptive studies are case studies, naturalistic observation, and surveys.

Query \(\PageIndex{1}\)

Query \(\PageIndex{2}\)

Query \(\PageIndex{3}\)

Query \(\PageIndex{4}\)

Case Studies

In 2011, the New York Times published a feature story on Krista and Tatiana Hogan, Canadian twin girls. These particular twins are unique because Krista and Tatiana are conjoined twins, connected at the head. There is evidence that the two girls are connected in a part of the brain called the thalamus, which is a major sensory relay center. Most incoming sensory information is sent through the thalamus before reaching higher regions of the cerebral cortex for processing.

Link to Learning

To learn more about Krista and Tatiana, watch this video about their lives as conjoined twins.

The implications of this potential connection mean that it might be possible for one twin to experience the sensations of the other twin. For instance, if Krista is watching a particularly funny television program, Tatiana might smile or laugh even if she is not watching the program. This particular possibility has piqued the interest of many neuroscientists who seek to understand how the brain uses sensory information.

These twins represent an enormous resource in the study of the brain, and since their condition is very rare, it is likely that as long as their family agrees, scientists will follow these girls very closely throughout their lives to gain as much information as possible (Dominus, 2011).

In observational research, scientists are conducting a clinical or case study when they focus on one person or just a few individuals. Indeed, some scientists spend their entire careers studying just 10–20 individuals. Why would they do this? Obviously, when they focus their attention on a very small number of people, they can gain a tremendous amount of insight into those cases. The richness of information that is collected in clinical or case studies is unmatched by any other single research method. This allows the researcher to have a very deep understanding of the individuals and the particular phenomenon being studied.

If clinical or case studies provide so much information, why are they not more frequent among researchers? As it turns out, the major benefit of this particular approach is also a weakness. As mentioned earlier, this approach is often used when studying individuals who are interesting to researchers because they have a rare characteristic. Therefore, the individuals who serve as the focus of case studies are not like most other people. If scientists ultimately want to explain all behavior, focusing attention on such a special group of people can make it difficult to generalize any observations to the larger population as a whole. Generalizing refers to the ability to apply the findings of a particular research project to larger segments of society. Again, case studies provide enormous amounts of information, but since the cases are so specific, the potential to apply what’s learned to the average person may be very limited.

Query \(\PageIndex{5}\)

Query \(\PageIndex{6}\)

Naturalistic Observation

If you want to understand how behavior occurs, one of the best ways to gain information is to simply observe the behavior in its natural context. However, people might change their behavior in unexpected ways if they know they are being observed. How do researchers obtain accurate information when people tend to hide their natural behavior? As an example, imagine that your professor asks everyone in your class to raise their hand if they always wash their hands after using the restroom. Chances are that almost everyone in the classroom will raise their hand, but do you think hand washing after every trip to the restroom is really that universal?

This is very similar to the phenomenon mentioned earlier in this module: many individuals do not feel comfortable answering a question honestly. But if we are committed to finding out the facts about hand washing, we have other options available to us.

Suppose we send a classmate into the restroom to actually watch whether everyone washes their hands after using the restroom. Will our observer blend into the restroom environment by wearing a white lab coat, sitting with a clipboard, and staring at the sinks? We want our researcher to be inconspicuous—perhaps standing at one of the sinks pretending to put in contact lenses while secretly recording the relevant information. This type of observational study is called naturalistic observation : observing behavior in its natural setting. To better understand peer exclusion, Suzanne Fanger collaborated with colleagues at the University of Texas to observe the behavior of preschool children on a playground. How did the observers remain inconspicuous over the duration of the study? They equipped a few of the children with wireless microphones (which the children quickly forgot about) and observed while taking notes from a distance. Also, the children in that particular preschool (a “laboratory preschool”) were accustomed to having observers on the playground (Fanger, Frankel, & Hazen, 2012).

It is critical that the observer be as unobtrusive and as inconspicuous as possible: when people know they are being watched, they are less likely to behave naturally. If you have any doubt about this, ask yourself how your driving behavior might differ in two situations: In the first situation, you are driving down a deserted highway during the middle of the day; in the second situation, you are being followed by a police car down the same deserted highway (Figure 1).

It should be pointed out that naturalistic observation is not limited to research involving humans. Indeed, some of the best-known examples of naturalistic observation involve researchers going into the field to observe various kinds of animals in their own environments. As with human studies, the researchers maintain their distance and avoid interfering with the animal subjects so as not to influence their natural behaviors. Scientists have used this technique to study social hierarchies and interactions among animals ranging from ground squirrels to gorillas. The information provided by these studies is invaluable in understanding how those animals organize socially and communicate with one another. The anthropologist Jane Goodall, for example, spent nearly five decades observing the behavior of chimpanzees in Africa (Figure 2). As an illustration of the types of concerns that a researcher might encounter in naturalistic observation, some scientists criticized Goodall for giving the chimps names instead of referring to them by numbers—using names was thought to undermine the emotional detachment required for the objectivity of the study (McKie, 2010).

The greatest benefit of naturalistic observation is the validity, or accuracy, of information collected unobtrusively in a natural setting. Having individuals behave as they normally would in a given situation means that we have a higher degree of ecological validity, or realism, than we might achieve with other research approaches. Therefore, our ability to generalize the findings of the research to real-world situations is enhanced. If done correctly, we need not worry about people or animals modifying their behavior simply because they are being observed. Sometimes, people may assume that reality programs give us a glimpse into authentic human behavior. However, the principle of inconspicuous observation is violated as reality stars are followed by camera crews and are interviewed on camera for personal confessionals. Given that environment, we must doubt how natural and realistic their behaviors are.

The major downside of naturalistic observation is that they are often difficult to set up and control. In our restroom study, what if you stood in the restroom all day prepared to record people’s hand washing behavior and no one came in? Or, what if you have been closely observing a troop of gorillas for weeks only to find that they migrated to a new place while you were sleeping in your tent? The benefit of realistic data comes at a cost. As a researcher you have no control of when (or if) you have behavior to observe. In addition, this type of observational research often requires significant investments of time, money, and a good dose of luck.

Sometimes studies involve structured observation. In these cases, people are observed while engaging in set, specific tasks. An excellent example of structured observation comes from Strange Situation by Mary Ainsworth (you will read more about this in the module on lifespan development). The Strange Situation is a procedure used to evaluate attachment styles that exist between an infant and caregiver. In this scenario, caregivers bring their infants into a room filled with toys. The Strange Situation involves a number of phases, including a stranger coming into the room, the caregiver leaving the room, and the caregiver’s return to the room. The infant’s behavior is closely monitored at each phase, but it is the behavior of the infant upon being reunited with the caregiver that is most telling in terms of characterizing the infant’s attachment style with the caregiver.

Another potential problem in observational research is observer bias . Generally, people who act as observers are closely involved in the research project and may unconsciously skew their observations to fit their research goals or expectations. To protect against this type of bias, researchers should have clear criteria established for the types of behaviors recorded and how those behaviors should be classified. In addition, researchers often compare observations of the same event by multiple observers, in order to test inter-rater reliability : a measure of reliability that assesses the consistency of observations by different observers.

Query \(\PageIndex{7}\)

Query \(\PageIndex{8}\)

Often, psychologists develop surveys as a means of gathering data. Surveys are lists of questions to be answered by research participants, and can be delivered as paper-and-pencil questionnaires, administered electronically, or conducted verbally (Figure 3). Generally, the survey itself can be completed in a short time, and the ease of administering a survey makes it easy to collect data from a large number of people.

Surveys allow researchers to gather data from larger samples than may be afforded by other research methods . A sample is a subset of individuals selected from a population , which is the overall group of individuals that the researchers are interested in. Researchers study the sample and seek to generalize their findings to the population.

There is both strength and weakness of the survey in comparison to case studies. By using surveys, we can collect information from a larger sample of people. A larger sample is better able to reflect the actual diversity of the population, thus allowing better generalizability. Therefore, if our sample is sufficiently large and diverse, we can assume that the data we collect from the survey can be generalized to the larger population with more certainty than the information collected through a case study. However, given the greater number of people involved, we are not able to collect the same depth of information on each person that would be collected in a case study.

Another potential weakness of surveys is something we touched on earlier in this module: people don’t always give accurate responses. They may lie, misremember, or answer questions in a way that they think makes them look good. For example, people may report drinking less alcohol than is actually the case.

Any number of research questions can be answered through the use of surveys. One real-world example is the research conducted by Jenkins, Ruppel, Kizer, Yehl, and Griffin (2012) about the backlash against the US Arab-American community following the terrorist attacks of September 11, 2001. Jenkins and colleagues wanted to determine to what extent these negative attitudes toward Arab-Americans still existed nearly a decade after the attacks occurred. In one study, 140 research participants filled out a survey with 10 questions, including questions asking directly about the participant’s overt prejudicial attitudes toward people of various ethnicities. The survey also asked indirect questions about how likely the participant would be to interact with a person of a given ethnicity in a variety of settings (such as, “How likely do you think it is that you would introduce yourself to a person of Arab-American descent?”). The results of the research suggested that participants were unwilling to report prejudicial attitudes toward any ethnic group. However, there were significant differences between their pattern of responses to questions about social interaction with Arab-Americans compared to other ethnic groups: they indicated less willingness for social interaction with Arab-Americans compared to the other ethnic groups. This suggested that the participants harbored subtle forms of prejudice against Arab-Americans, despite their assertions that this was not the case (Jenkins et al., 2012).

Query \(\PageIndex{9}\)

Query \(\PageIndex{10}\)

Query \(\PageIndex{11}\)

Query \(\PageIndex{12}\)

Query \(\PageIndex{13}\)

Think It Over

A friend of yours is working part-time in a local pet store. Your friend has become increasingly interested in how dogs normally communicate and interact with each other, and is thinking of visiting a local veterinary clinic to see how dogs interact in the waiting room. After reading this section, do you think this is the best way to better understand such interactions? Do you have any suggestions that might result in more valid data?

clinical or case study:  observational research study focusing on one or a few people

correlational research:  tests whether a relationship exists between two or more variables

descriptive research:  research studies that do not test specific relationships between variables; they are used to describe general or specific behaviors and attributes that are observed and measured

experimental research:  tests a hypothesis to determine cause and effect relationships

generalize inferring that the results for a sample apply to the larger population

inter-rater reliability:  measure of agreement among observers on how they record and classify a particular event

naturalistic observation:  observation of behavior in its natural setting

observer bias:  when observations may be skewed to align with observer expectations

population:  overall group of individuals that the researchers are interested in

sample:  subset of individuals selected from the larger population

survey:  list of questions to be answered by research participants—given as paper-and-pencil questionnaires, administered electronically, or conducted verbally—allowing researchers to collect data from a large number of people

Licenses and Attributions

CC licensed content, Original

• Modification and adaptation. Provided by : Lumen Learning. License : CC BY-SA: Attribution-ShareAlike
• Approaches to Research. Authored by : OpenStax College. Located at : http://cnx.org/contents/[email protected]:iMyFZJzg@5/Approaches-to-Research . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Descriptive Research. Provided by : Boundless. Located at : https://www.boundless.com/psychology/textbooks/boundless-psychology-textbook/researching-psychology-2/types-of-research-studies-27/descriptive-research-124-12659/ . License : CC BY-SA: Attribution-ShareAlike

Using Science to Inform Educational Practices

Descriptive Research

There are many research methods available to psychologists in their efforts to understand, describe, and explain behavior. Some methods rely on observational techniques. Other approaches involve interactions between the researcher and the individuals who are being studied—ranging from a series of simple questions to extensive, in-depth interviews—to well-controlled experiments. The main categories of psychological research are descriptive, correlational, and experimental research. Each of these research methods has unique strengths and weaknesses, and each method may only be appropriate for certain types of research questions.

Research studies that do not test specific relationships between variables are called  descriptive studies . For this method, the research question or hypothesis can be about a single variable (e.g., How accurate are people’s first impressions?) or can be a broad and exploratory question (e.g., What is it like to be a working mother diagnosed with depression?). The variable of the study is measured and reported without any further relationship analysis. A researcher might choose this method if they only needed to report information, such as a tally, an average, or a list of responses. Descriptive research can answer interesting and important questions, but what it cannot do is answer questions about relationships between variables.

Video 2.4.1.  Descriptive Research Design  provides explanation and examples for quantitative descriptive research. A closed-captioned version of this video is available here .

Descriptive research is distinct from  correlational research , in which researchers formally test whether a relationship exists between two or more variables.  Experimental research  goes a step further beyond descriptive and correlational research and randomly assigns people to different conditions, using hypothesis testing to make inferences about causal relationships between variables. We will discuss each of these methods more in-depth later.

Table 2.4.1. Comparison of research design methods

Candela Citations

• Descriptive Research. Authored by : Nicole Arduini-Van Hoose. Provided by : Hudson Valley Community College. Retrieved from : https://courses.lumenlearning.com/edpsy/chapter/descriptive-research/. License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
• Descriptive Research. Authored by : Nicole Arduini-Van Hoose. Provided by : Hudson Valley Community College. Retrieved from : https://courses.lumenlearning.com/adolescent/chapter/descriptive-research/. License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike

Educational Psychology Copyright © 2020 by Nicole Arduini-Van Hoose is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Hypothesis tests

• Author information
• Article notes
• Copyright and License information

Accepted 2019 Mar 28; Issue date 2019 Jul.

Key points.

Hypothesis tests are used to assess whether a difference between two samples represents a real difference between the populations from which the samples were taken.

A null hypothesis of ‘no difference’ is taken as a starting point, and we calculate the probability that both sets of data came from the same population. This probability is expressed as a p -value.

When the null hypothesis is false, p- values tend to be small. When the null hypothesis is true, any p- value is equally likely.

Learning objectives.

By reading this article, you should be able to:

Explain why hypothesis testing is used.

Use a table to determine which hypothesis test should be used for a particular situation.

Interpret a p- value.

A hypothesis test is a procedure used in statistics to assess whether a particular viewpoint is likely to be true. They follow a strict protocol, and they generate a ‘ p- value’, on the basis of which a decision is made about the truth of the hypothesis under investigation. All of the routine statistical ‘tests’ used in research— t- tests, χ 2 tests, Mann–Whitney tests, etc.—are all hypothesis tests, and in spite of their differences they are all used in essentially the same way. But why do we use them at all?

Comparing the heights of two individuals is easy: we can measure their height in a standardised way and compare them. When we want to compare the heights of two small well-defined groups (for example two groups of children), we need to use a summary statistic that we can calculate for each group. Such summaries (means, medians, etc.) form the basis of descriptive statistics, and are well described elsewhere. 1 However, a problem arises when we try to compare very large groups or populations: it may be impractical or even impossible to take a measurement from everyone in the population, and by the time you do so, the population itself will have changed. A similar problem arises when we try to describe the effects of drugs—for example by how much on average does a particular vasopressor increase MAP?

To solve this problem, we use random samples to estimate values for populations. By convention, the values we calculate from samples are referred to as statistics and denoted by Latin letters ( x ¯ for sample mean; SD for sample standard deviation) while the unknown population values are called parameters , and denoted by Greek letters (μ for population mean, σ for population standard deviation).

Inferential statistics describes the methods we use to estimate population parameters from random samples; how we can quantify the level of inaccuracy in a sample statistic; and how we can go on to use these estimates to compare populations.

Sampling error

There are many reasons why a sample may give an inaccurate picture of the population it represents: it may be biased, it may not be big enough, and it may not be truly random. However, even if we have been careful to avoid these pitfalls, there is an inherent difference between the sample and the population at large. To illustrate this, let us imagine that the actual average height of males in London is 174 cm. If I were to sample 100 male Londoners and take a mean of their heights, I would be very unlikely to get exactly 174 cm. Furthermore, if somebody else were to perform the same exercise, it would be unlikely that they would get the same answer as I did. The sample mean is different each time it is taken, and the way it differs from the actual mean of the population is described by the standard error of the mean (standard error, or SEM ). The standard error is larger if there is a lot of variation in the population, and becomes smaller as the sample size increases. It is calculated thus:

where SD is the sample standard deviation, and n is the sample size.

As errors are normally distributed, we can use this to estimate a 95% confidence interval on our sample mean as follows:

We can interpret this as meaning ‘We are 95% confident that the actual mean is within this range.’

Some confusion arises at this point between the SD and the standard error. The SD is a measure of variation in the sample. The range x ¯ ± ( 1.96 × SD ) will normally contain 95% of all your data. It can be used to illustrate the spread of the data and shows what values are likely. In contrast, standard error tells you about the precision of the mean and is used to calculate confidence intervals.

One straightforward way to compare two samples is to use confidence intervals. If we calculate the mean height of two groups and find that the 95% confidence intervals do not overlap, this can be taken as evidence of a difference between the two means. This method of statistical inference is reasonably intuitive and can be used in many situations. 2 Many journals, however, prefer to report inferential statistics using p -values.

Inference testing using a null hypothesis

In 1925, the British statistician R.A. Fisher described a technique for comparing groups using a null hypothesis , a method which has dominated statistical comparison ever since. The technique itself is rather straightforward, but often gets lost in the mechanics of how it is done. To illustrate, imagine we want to compare the HR of two different groups of people. We take a random sample from each group, which we call our data. Then:

Assume that both samples came from the same group. This is our ‘null hypothesis’.

Calculate the probability that an experiment would give us these data, assuming that the null hypothesis is true. We express this probability as a p- value, a number between 0 and 1, where 0 is ‘impossible’ and 1 is ‘certain’.

If the probability of the data is low, we reject the null hypothesis and conclude that there must be a difference between the two groups.

Formally, we can define a p- value as ‘the probability of finding the observed result or a more extreme result, if the null hypothesis were true.’ Standard practice is to set a cut-off at p <0.05 (this cut-off is termed the alpha value). If the null hypothesis were true, a result such as this would only occur 5% of the time or less; this in turn would indicate that the null hypothesis itself is unlikely. Fisher described the process as follows: ‘Set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance.’ 3 This probably remains the most succinct description of the procedure.

A question which often arises at this point is ‘Why do we use a null hypothesis?’ The simple answer is that it is easy: we can readily describe what we would expect of our data under a null hypothesis, we know how data would behave, and we can readily work out the probability of getting the result that we did. It therefore makes a very simple starting point for our probability assessment. All probabilities require a set of starting conditions, in much the same way that measuring the distance to London needs a starting point. The null hypothesis can be thought of as an easy place to put the start of your ruler.

If a null hypothesis is rejected, an alternate hypothesis must be adopted in its place. The null and alternate hypotheses must be mutually exclusive, but must also between them describe all situations. If a null hypothesis is ‘no difference exists’ then the alternate should be simply ‘a difference exists’.

Hypothesis testing in practice

The components of a hypothesis test can be readily described using the acronym GOST: identify the Groups you wish to compare; define the Outcome to be measured; collect and Summarise the data; then evaluate the likelihood of the null hypothesis, using a Test statistic .

When considering groups, think first about how many. Is there just one group being compared against an audit standard, or are you comparing one group with another? Some studies may wish to compare more than two groups. Another situation may involve a single group measured at different points in time, for example before or after a particular treatment. In this situation each participant is compared with themselves, and this is often referred to as a ‘paired’ or a ‘repeated measures’ design. It is possible to combine these types of groups—for example a researcher may measure arterial BP on a number of different occasions in five different groups of patients. Such studies can be difficult, both to analyse and interpret.

In other studies we may want to see how a continuous variable (such as age or height) affects the outcomes. These techniques involve regression analysis, and are beyond the scope of this article.

The outcome measures are the data being collected. This may be a continuous measure, such as temperature or BMI, or it may be a categorical measure, such as ASA status or surgical specialty. Often, inexperienced researchers will strive to collect lots of outcome measures in an attempt to find something that differs between the groups of interest; if this is done, a ‘primary outcome measure’ should be identified before the research begins. In addition, the results of any hypothesis tests will need to be corrected for multiple measures.

The summary and the test statistic will be defined by the type of data that have been collected. The test statistic is calculated then transformed into a p- value using tables or software. It is worth looking at two common tests in a little more detail: the χ 2 test, and the t -test.

Categorical data: the χ 2 test

The χ 2 test of independence is a test for comparing categorical outcomes in two or more groups. For example, a number of trials have compared surgical site infections in patients who have been given different concentrations of oxygen perioperatively. In the PROXI trial, 4 685 patients received oxygen 80%, and 701 patients received oxygen 30%. In the 80% group there were 131 infections, while in the 30% group there were 141 infections. In this study, the groups were oxygen 80% and oxygen 30%, and the outcome measure was the presence of a surgical site infection.

The summary is a table ( Table 1 ), and the hypothesis test compares this table (the ‘observed’ table) with the table that would be expected if the proportion of infections in each group was the same (the ‘expected’ table). The test statistic is χ 2 , from which a p- value is calculated. In this instance the p -value is 0.64, which means that results like this would occur 64% of the time if the null hypothesis were true. We thus have no evidence to reject the null hypothesis; the observed difference probably results from sampling variation rather than from an inherent difference between the two groups.

Summary of the results of the PROXI trial. Figures are numbers of patients.

Continuous data: the t- test

The t- test is a statistical method for comparing means, and is one of the most widely used hypothesis tests. Imagine a study where we try to see if there is a difference in the onset time of a new neuromuscular blocking agent compared with suxamethonium. We could enlist 100 volunteers, give them a general anaesthetic, and randomise 50 of them to receive the new drug and 50 of them to receive suxamethonium. We then time how long it takes (in seconds) to have ideal intubation conditions, as measured by a quantitative nerve stimulator. Our data are therefore a list of times. In this case, the groups are ‘new drug’ and suxamethonium, and the outcome is time, measured in seconds. This can be summarised by using means; the hypothesis test will compare the means of the two groups, using a p- value calculated from a ‘ t statistic’. Hopefully it is becoming obvious at this point that the test statistic is usually identified by a letter, and this letter is often cited in the name of the test.

The t -test comes in a number of guises, depending on the comparison being made. A single sample can be compared with a standard (Is the BMI of school leavers in this town different from the national average?); two samples can be compared with each other, as in the example above; or the same study subjects can be measured at two different times. The latter case is referred to as a paired t- test, because each participant provides a pair of measurements—such as in a pre- or postintervention study.

A large number of methods for testing hypotheses exist; the commonest ones and their uses are described in Table 2 . In each case, the test can be described by detailing the groups being compared ( Table 2 , columns) the outcome measures (rows), the summary, and the test statistic. The decision to use a particular test or method should be made during the planning stages of a trial or experiment. At this stage, an estimate needs to be made of how many test subjects will be needed. Such calculations are described in detail elsewhere. 5

The principle types of hypothesis test. Tests comparing more than two samples can indicate that one group differs from the others, but will not identify which. Subsequent ‘post hoc’ testing is required if a difference is found.

Controversies surrounding hypothesis testing

Although hypothesis tests have been the basis of modern science since the middle of the 20th century, they have been plagued by misconceptions from the outset; this has led to what has been described as a crisis in science in the last few years: some journals have gone so far as to ban p -value s outright. 6 This is not because of any flaw in the concept of a p -value, but because of a lack of understanding of what they mean.

Possibly the most pervasive misunderstanding is the belief that the p- value is the chance that the null hypothesis is true, or that the p- value represents the frequency with which you will be wrong if you reject the null hypothesis (i.e. claim to have found a difference). This interpretation has frequently made it into the literature, and is a very easy trap to fall into when discussing hypothesis tests. To avoid this, it is important to remember that the p- value is telling us something about our sample , not about the null hypothesis. Put in simple terms, we would like to know the probability that the null hypothesis is true, given our data. The p- value tells us the probability of getting these data if the null hypothesis were true, which is not the same thing. This fallacy is referred to as ‘flipping the conditional’; the probability of an outcome under certain conditions is not the same as the probability of those conditions given that the outcome has happened.

A useful example is to imagine a magic trick in which you select a card from a normal deck of 52 cards, and the performer reveals your chosen card in a surprising manner. If the performer were relying purely on chance, this would only happen on average once in every 52 attempts. On the basis of this, we conclude that it is unlikely that the magician is simply relying on chance. Although simple, we have just performed an entire hypothesis test. We have declared a null hypothesis (the performer was relying on chance); we have even calculated a p -value (1 in 52, ≈0.02); and on the basis of this low p- value we have rejected our null hypothesis. We would, however, be wrong to suggest that there is a probability of 0.02 that the performer is relying on chance—that is not what our figure of 0.02 is telling us.

To explore this further we can create two populations, and watch what happens when we use simulation to take repeated samples to compare these populations. Computers allow us to do this repeatedly, and to see what p- value s are generated (see Supplementary online material). 7 Fig 1 illustrates the results of 100,000 simulated t -tests, generated in two set of circumstances. In Fig 1 a , we have a situation in which there is a difference between the two populations. The p- value s cluster below the 0.05 cut-off, although there is a small proportion with p >0.05. Interestingly, the proportion of comparisons where p <0.05 is 0.8 or 80%, which is the power of the study (the sample size was specifically calculated to give a power of 80%).

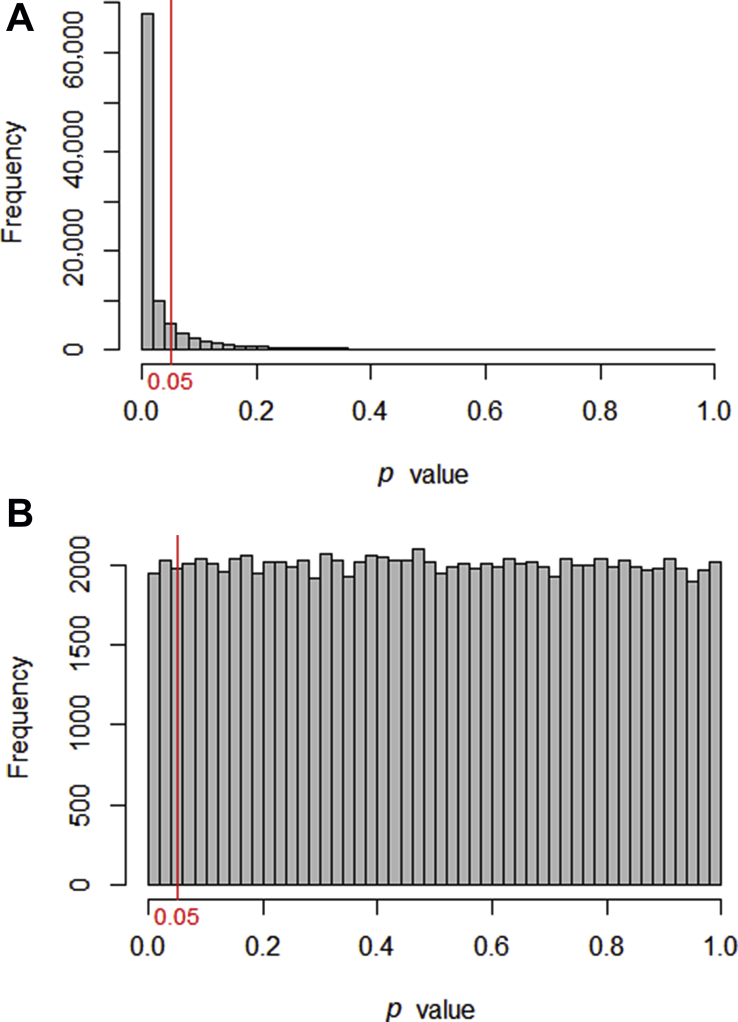
The p- value s generated when 100,000 t -tests are used to compare two samples taken from defined populations. ( a ) The populations have a difference and the p- value s are mostly significant. ( b ) The samples were taken from the same population (i.e. the null hypothesis is true) and the p- value s are distributed uniformly.

Figure 1 b depicts the situation where repeated samples are taken from the same parent population (i.e. the null hypothesis is true). Somewhat surprisingly, all p- value s occur with equal frequency, with p <0.05 occurring exactly 5% of the time. Thus, when the null hypothesis is true, a type I error will occur with a frequency equal to the alpha significance cut-off.

Figure 1 highlights the underlying problem: when presented with a p -value <0.05, is it possible with no further information, to determine whether you are looking at something from Fig 1 a or Fig 1 b ?

Finally, it cannot be stressed enough that although hypothesis testing identifies whether or not a difference is likely, it is up to us as clinicians to decide whether or not a statistically significant difference is also significant clinically.

Hypothesis testing: what next?

As mentioned above, some have suggested moving away from p -values, but it is not entirely clear what we should use instead. Some sources have advocated focussing more on effect size; however, without a measure of significance we have merely returned to our original problem: how do we know that our difference is not just a result of sampling variation?

One solution is to use Bayesian statistics. Up until very recently, these techniques have been considered both too difficult and not sufficiently rigorous. However, recent advances in computing have led to the development of Bayesian equivalents of a number of standard hypothesis tests. 8 These generate a ‘Bayes Factor’ (BF), which tells us how more (or less) likely the alternative hypothesis is after our experiment. A BF of 1.0 indicates that the likelihood of the alternate hypothesis has not changed. A BF of 10 indicates that the alternate hypothesis is 10 times more likely than we originally thought. A number of classifications for BF exist; greater than 10 can be considered ‘strong evidence’, while BF greater than 100 can be classed as ‘decisive’.

Figures such as the BF can be quoted in conjunction with the traditional p- value, but it remains to be seen whether they will become mainstream.

Declaration of interest

The author declares that they have no conflict of interest.

The associated MCQs (to support CME/CPD activity) will be accessible at www.bjaed.org/cme/home by subscribers to BJA Education .

Jason Walker FRCA FRSS BSc (Hons) Math Stat is a consultant anaesthetist at Ysbyty Gwynedd Hospital, Bangor, Wales, and an honorary senior lecturer at Bangor University. He is vice chair of his local research ethics committee, and an examiner for the Primary FRCA.

Matrix codes: 1A03, 2A04, 3J03

Supplementary data to this article can be found online at https://doi.org/10.1016/j.bjae.2019.03.006 .

Supplementary material

The following is the Supplementary data to this article:

• 1. McCluskey A., Lalkhen A.G. Statistics II: central tendency and spread of data. CEACCP. 2007;7:127–130. [ Google Scholar ]
• 2. Altman D.G., Machin D., Bryant T.N., Gardner M.J. 2nd Edn. BMJ Books; London: 2000. Statistics with confidence. [ Google Scholar ]
• 3. Fisher R.A. The arrangement of field experiments. J Min Agric Gr Br. 1926;33:503–513. [ Google Scholar ]
• 4. Meyhoff C.S., Wetterslev J., Jorgensen L.N. Effect of high perioperative oxygen fraction on surgical site infection and pulmonary complications after abdominal surgery: the PROXI randomized clinical trial. JAMA. 2009;302:1543–1550. doi: 10.1001/jama.2009.1452. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Columb M.O., Atkinson M.S. Statistical analysis: sample size and power estimations. BJA Educ. 2016;16:159–161. [ Google Scholar ]
• 6. Trafimow D., Marks M. Editorial. Basic Appl Soc Psych. 2015;37:1–2. [ Google Scholar ]
• 7. Colquhoun D. An investigation of the false discovery rate and the misinterpretation of p-values. R Soc Open Sci. 2014;1:140216. doi: 10.1098/rsos.140216. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 8. Ly A., Verhagen J., Wagenmakers E. Harold Jeffreys’s default Bayes factor hypothesis tests: explanation, extension, and application in psychology. J Math Psychol. 2016;72:19–32. [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

• View on publisher site
• PDF (344.3 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections