define hypothesis testing function

• Hypothesis Testing: Definition, Uses, Limitations + Examples

Hypothesis testing is as old as the scientific method and is at the heart of the research process. 

Research exists to validate or disprove assumptions about various phenomena. The process of validation involves testing and it is in this context that we will explore hypothesis testing. 

What is a Hypothesis? 

A hypothesis is a calculated prediction or assumption about a population parameter based on limited evidence. The whole idea behind hypothesis formulation is testing—this means the researcher subjects his or her calculated assumption to a series of evaluations to know whether they are true or false. 

Typically, every research starts with a hypothesis—the investigator makes a claim and experiments to prove that this claim is true or false . For instance, if you predict that students who drink milk before class perform better than those who don’t, then this becomes a hypothesis that can be confirmed or refuted using an experiment.  

Read: What is Empirical Research Study? [Examples & Method]

What are the Types of Hypotheses? 

1. simple hypothesis.

Also known as a basic hypothesis, a simple hypothesis suggests that an independent variable is responsible for a corresponding dependent variable. In other words, an occurrence of the independent variable inevitably leads to an occurrence of the dependent variable. 

Typically, simple hypotheses are considered as generally true, and they establish a causal relationship between two variables. 

Examples of Simple Hypothesis  

• Drinking soda and other sugary drinks can cause obesity. 
• Smoking cigarettes daily leads to lung cancer.

2. Complex Hypothesis

A complex hypothesis is also known as a modal. It accounts for the causal relationship between two independent variables and the resulting dependent variables. This means that the combination of the independent variables leads to the occurrence of the dependent variables . 

Examples of Complex Hypotheses  

• Adults who do not smoke and drink are less likely to develop liver-related conditions.
• Global warming causes icebergs to melt which in turn causes major changes in weather patterns.

3. Null Hypothesis

As the name suggests, a null hypothesis is formed when a researcher suspects that there’s no relationship between the variables in an observation. In this case, the purpose of the research is to approve or disapprove this assumption. 

Examples of Null Hypothesis

• This is no significant change in a student’s performance if they drink coffee or tea before classes. 
• There’s no significant change in the growth of a plant if one uses distilled water only or vitamin-rich water. 

Read: Research Report: Definition, Types + [Writing Guide]

4. Alternative Hypothesis 

To disapprove a null hypothesis, the researcher has to come up with an opposite assumption—this assumption is known as the alternative hypothesis. This means if the null hypothesis says that A is false, the alternative hypothesis assumes that A is true. 

An alternative hypothesis can be directional or non-directional depending on the direction of the difference. A directional alternative hypothesis specifies the direction of the tested relationship, stating that one variable is predicted to be larger or smaller than the null value while a non-directional hypothesis only validates the existence of a difference without stating its direction. 

Examples of Alternative Hypotheses  

• Starting your day with a cup of tea instead of a cup of coffee can make you more alert in the morning. 
• The growth of a plant improves significantly when it receives distilled water instead of vitamin-rich water. 

5. Logical Hypothesis

Logical hypotheses are some of the most common types of calculated assumptions in systematic investigations. It is an attempt to use your reasoning to connect different pieces in research and build a theory using little evidence. In this case, the researcher uses any data available to him, to form a plausible assumption that can be tested. 

Examples of Logical Hypothesis

• Waking up early helps you to have a more productive day. 
• Beings from Mars would not be able to breathe the air in the atmosphere of the Earth. 

6. Empirical Hypothesis  

After forming a logical hypothesis, the next step is to create an empirical or working hypothesis. At this stage, your logical hypothesis undergoes systematic testing to prove or disprove the assumption. An empirical hypothesis is subject to several variables that can trigger changes and lead to specific outcomes. 

Examples of Empirical Testing 

• People who eat more fish run faster than people who eat meat.
• Women taking vitamin E grow hair faster than those taking vitamin K.

7. Statistical Hypothesis

When forming a statistical hypothesis, the researcher examines the portion of a population of interest and makes a calculated assumption based on the data from this sample. A statistical hypothesis is most common with systematic investigations involving a large target audience. Here, it’s impossible to collect responses from every member of the population so you have to depend on data from your sample and extrapolate the results to the wider population. 

Examples of Statistical Hypothesis  

• 45% of students in Louisiana have middle-income parents. 
• 80% of the UK’s population gets a divorce because of irreconcilable differences.

What is Hypothesis Testing? 

Hypothesis testing is an assessment method that allows researchers to determine the plausibility of a hypothesis. It involves testing an assumption about a specific population parameter to know whether it’s true or false. These population parameters include variance, standard deviation, and median. 

Typically, hypothesis testing starts with developing a null hypothesis and then performing several tests that support or reject the null hypothesis. The researcher uses test statistics to compare the association or relationship between two or more variables. 

Explore: Research Bias: Definition, Types + Examples

Researchers also use hypothesis testing to calculate the coefficient of variation and determine if the regression relationship and the correlation coefficient are statistically significant.

How Hypothesis Testing Works

The basis of hypothesis testing is to examine and analyze the null hypothesis and alternative hypothesis to know which one is the most plausible assumption. Since both assumptions are mutually exclusive, only one can be true. In other words, the occurrence of a null hypothesis destroys the chances of the alternative coming to life, and vice-versa. 

Interesting: 21 Chrome Extensions for Academic Researchers in 2021

What Are The Stages of Hypothesis Testing?  

To successfully confirm or refute an assumption, the researcher goes through five (5) stages of hypothesis testing; 

• Determine the null hypothesis
• Specify the alternative hypothesis
• Set the significance level
• Calculate the test statistics and corresponding P-value
• Draw your conclusion
• Determine the Null Hypothesis

Like we mentioned earlier, hypothesis testing starts with creating a null hypothesis which stands as an assumption that a certain statement is false or implausible. For example, the null hypothesis (H0) could suggest that different subgroups in the research population react to a variable in the same way. 

• Specify the Alternative Hypothesis

Once you know the variables for the null hypothesis, the next step is to determine the alternative hypothesis. The alternative hypothesis counters the null assumption by suggesting the statement or assertion is true. Depending on the purpose of your research, the alternative hypothesis can be one-sided or two-sided. 

Using the example we established earlier, the alternative hypothesis may argue that the different sub-groups react differently to the same variable based on several internal and external factors. 

• Set the Significance Level

Many researchers create a 5% allowance for accepting the value of an alternative hypothesis, even if the value is untrue. This means that there is a 0.05 chance that one would go with the value of the alternative hypothesis, despite the truth of the null hypothesis. 

Something to note here is that the smaller the significance level, the greater the burden of proof needed to reject the null hypothesis and support the alternative hypothesis.

Explore: What is Data Interpretation? + [Types, Method & Tools]

• Calculate the Test Statistics and Corresponding P-Value 

Test statistics in hypothesis testing allow you to compare different groups between variables while the p-value accounts for the probability of obtaining sample statistics if your null hypothesis is true. In this case, your test statistics can be the mean, median and similar parameters. 

If your p-value is 0.65, for example, then it means that the variable in your hypothesis will happen 65 in100 times by pure chance. Use this formula to determine the p-value for your data: 

• Draw Your Conclusions

After conducting a series of tests, you should be able to agree or refute the hypothesis based on feedback and insights from your sample data.  

Applications of Hypothesis Testing in Research

Hypothesis testing isn’t only confined to numbers and calculations; it also has several real-life applications in business, manufacturing, advertising, and medicine. 

In a factory or other manufacturing plants, hypothesis testing is an important part of quality and production control before the final products are approved and sent out to the consumer. 

During ideation and strategy development, C-level executives use hypothesis testing to evaluate their theories and assumptions before any form of implementation. For example, they could leverage hypothesis testing to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales. 

In addition, hypothesis testing is used during clinical trials to prove the efficacy of a drug or new medical method before its approval for widespread human usage. 

What is an Example of Hypothesis Testing?

An employer claims that her workers are of above-average intelligence. She takes a random sample of 20 of them and gets the following results: 

Mean IQ Scores: 110

Standard Deviation: 15 

Mean Population IQ: 100

Step 1: Using the value of the mean population IQ, we establish the null hypothesis as 100.

Step 2: State that the alternative hypothesis is greater than 100.

Step 3: State the alpha level as 0.05 or 5% 

Step 4: Find the rejection region area (given by your alpha level above) from the z-table. An area of .05 is equal to a z-score of 1.645.

Step 5: Calculate the test statistics using this formula

Z = (110–100) ÷ (15÷√20) 

10 ÷ 3.35 = 2.99 

If the value of the test statistics is higher than the value of the rejection region, then you should reject the null hypothesis. If it is less, then you cannot reject the null. 

In this case, 2.99 > 1.645 so we reject the null. 

Importance/Benefits of Hypothesis Testing 

The most significant benefit of hypothesis testing is it allows you to evaluate the strength of your claim or assumption before implementing it in your data set. Also, hypothesis testing is the only valid method to prove that something “is or is not”. Other benefits include: 

• Hypothesis testing provides a reliable framework for making any data decisions for your population of interest. 
• It helps the researcher to successfully extrapolate data from the sample to the larger population. 
• Hypothesis testing allows the researcher to determine whether the data from the sample is statistically significant. 
• Hypothesis testing is one of the most important processes for measuring the validity and reliability of outcomes in any systematic investigation. 
• It helps to provide links to the underlying theory and specific research questions.

Criticism and Limitations of Hypothesis Testing

Several limitations of hypothesis testing can affect the quality of data you get from this process. Some of these limitations include: 

• The interpretation of a p-value for observation depends on the stopping rule and definition of multiple comparisons. This makes it difficult to calculate since the stopping rule is subject to numerous interpretations, plus “multiple comparisons” are unavoidably ambiguous. 
• Conceptual issues often arise in hypothesis testing, especially if the researcher merges Fisher and Neyman-Pearson’s methods which are conceptually distinct. 
• In an attempt to focus on the statistical significance of the data, the researcher might ignore the estimation and confirmation by repeated experiments.
• Hypothesis testing can trigger publication bias, especially when it requires statistical significance as a criterion for publication.
• When used to detect whether a difference exists between groups, hypothesis testing can trigger absurd assumptions that affect the reliability of your observation.

Connect to Formplus, Get Started Now - It's Free!

• alternative hypothesis
• alternative vs null hypothesis
• complex hypothesis
• empirical hypothesis
• hypothesis testing
• logical hypothesis
• simple hypothesis
• statistical hypothesis
• busayo.longe

You may also like:

Alternative vs Null Hypothesis: Pros, Cons, Uses & Examples

We are going to discuss alternative hypotheses and null hypotheses in this post and how they work in research.

Internal Validity in Research: Definition, Threats, Examples

In this article, we will discuss the concept of internal validity, some clear examples, its importance, and how to test it.

What is Pure or Basic Research? + [Examples & Method]

Simple guide on pure or basic research, its methods, characteristics, advantages, and examples in science, medicine, education and psychology

Type I vs Type II Errors: Causes, Examples & Prevention

This article will discuss the two different types of errors in hypothesis testing and how you can prevent them from occurring in your research

Formplus - For Seamless Data Collection

Collect data the right way with a versatile data collection tool. try formplus and transform your work productivity today..

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

• We first choose a significance level ($α$), which sets a threshold for making decisions.

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

• --> Statistics -->

--> F Statistic Formula – Explained -->

--> correlation – connecting the dots, the role of correlation in data analysis -->, --> hypothesis testing – a deep dive into hypothesis testing, the backbone of statistical inference -->, --> sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions -->, --> law of large numbers – a deep dive into the world of statistics -->, --> central limit theorem – a deep dive into central limit theorem and its significance in statistics -->, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

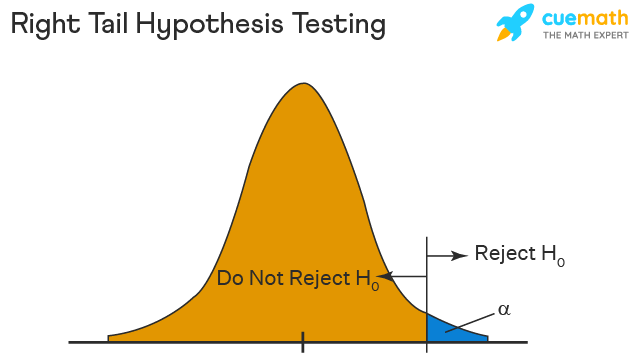
Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

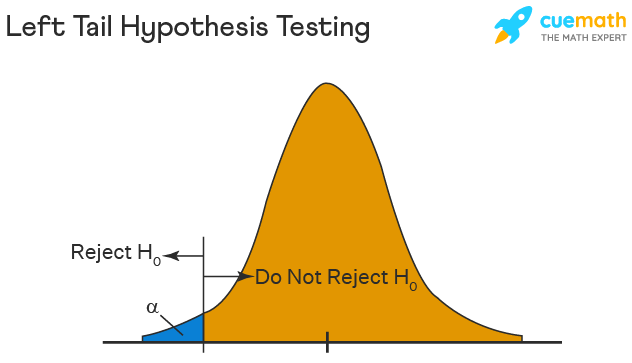
The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

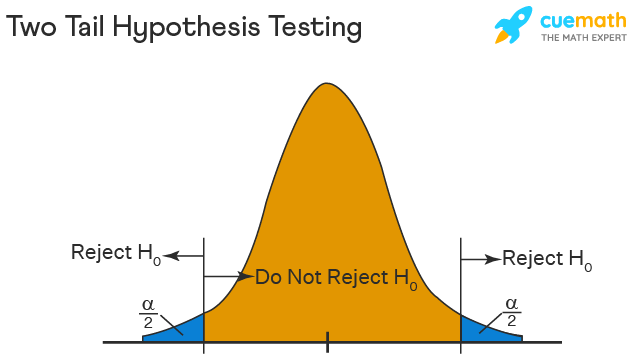
In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

• Data Science
• Data Analysis
• Data Visualization
• Machine Learning
• Deep Learning
• Computer Vision
• Artificial Intelligence
• AI ML DS Interview Series
• AI ML DS Projects series
• Data Engineering
• Web Scrapping

Hypothesis in Machine Learning

The concept of a hypothesis is fundamental in Machine Learning and data science endeavours. In the realm of machine learning, a hypothesis serves as an initial assumption made by data scientists and ML professionals when attempting to address a problem. Machine learning involves conducting experiments based on past experiences, and these hypotheses are crucial in formulating potential solutions.

It’s important to note that in machine learning discussions, the terms “hypothesis” and “model” are sometimes used interchangeably. However, a hypothesis represents an assumption, while a model is a mathematical representation employed to test that hypothesis. This section on “Hypothesis in Machine Learning” explores key aspects related to hypotheses in machine learning and their significance.

Table of Content

How does a Hypothesis work?

Hypothesis space and representation in machine learning, hypothesis in statistics, faqs on hypothesis in machine learning.

A hypothesis in machine learning is the model’s presumption regarding the connection between the input features and the result. It is an illustration of the mapping function that the algorithm is attempting to discover using the training set. To minimize the discrepancy between the expected and actual outputs, the learning process involves modifying the weights that parameterize the hypothesis. The objective is to optimize the model’s parameters to achieve the best predictive performance on new, unseen data, and a cost function is used to assess the hypothesis’ accuracy.

In most supervised machine learning algorithms, our main goal is to find a possible hypothesis from the hypothesis space that could map out the inputs to the proper outputs. The following figure shows the common method to find out the possible hypothesis from the Hypothesis space:

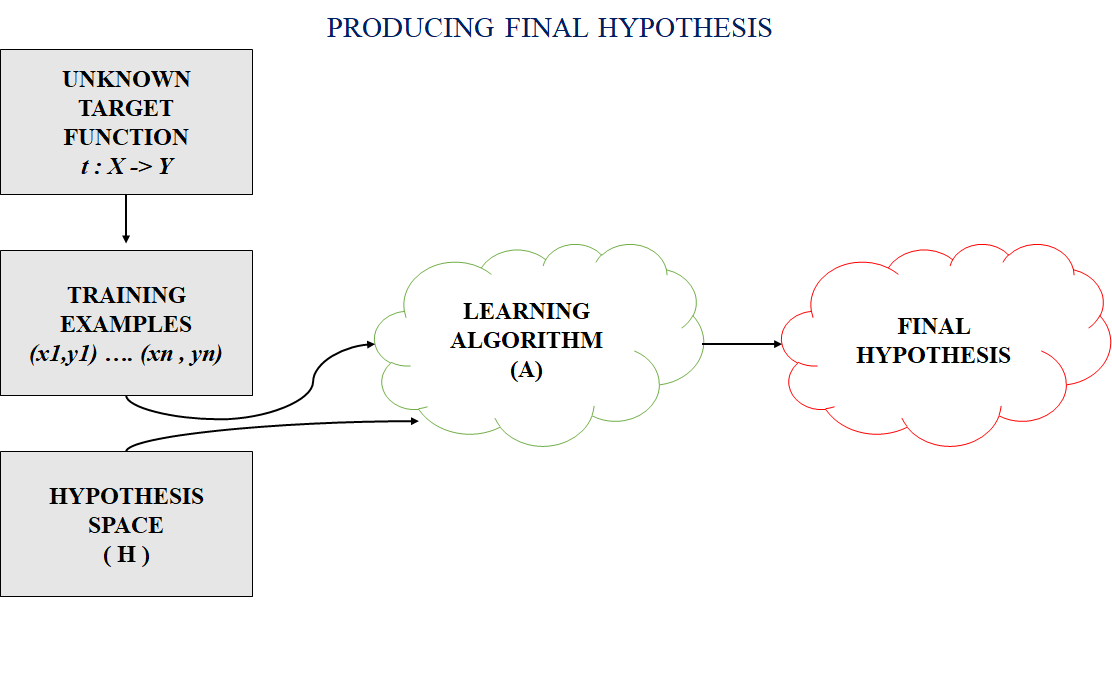
Hypothesis Space (H)

Hypothesis space is the set of all the possible legal hypothesis. This is the set from which the machine learning algorithm would determine the best possible (only one) which would best describe the target function or the outputs.

Hypothesis (h)

A hypothesis is a function that best describes the target in supervised machine learning. The hypothesis that an algorithm would come up depends upon the data and also depends upon the restrictions and bias that we have imposed on the data.

The Hypothesis can be calculated as:

[Tex]y = mx + b [/Tex]

• m = slope of the lines
• b = intercept

To better understand the Hypothesis Space and Hypothesis consider the following coordinate that shows the distribution of some data:

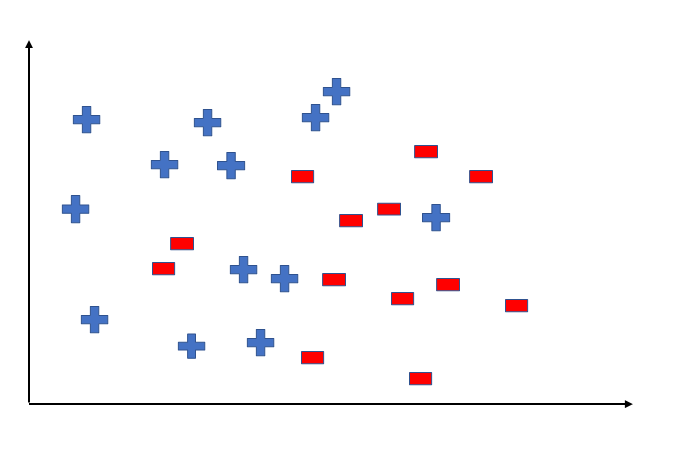
Say suppose we have test data for which we have to determine the outputs or results. The test data is as shown below:

We can predict the outcomes by dividing the coordinate as shown below:

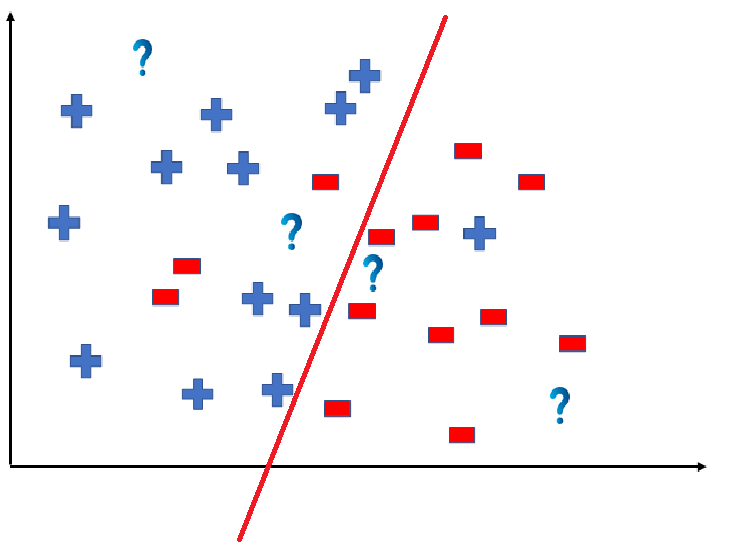
So the test data would yield the following result:

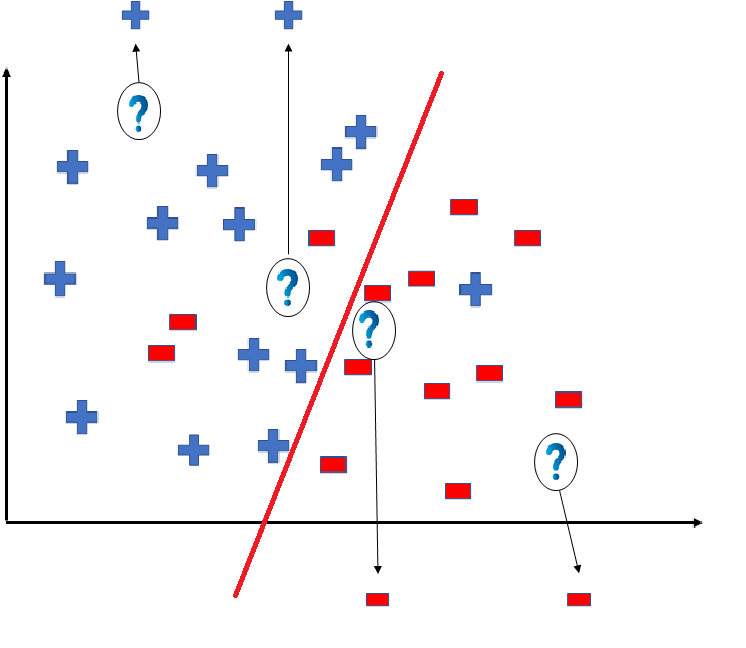
But note here that we could have divided the coordinate plane as:

The way in which the coordinate would be divided depends on the data, algorithm and constraints.

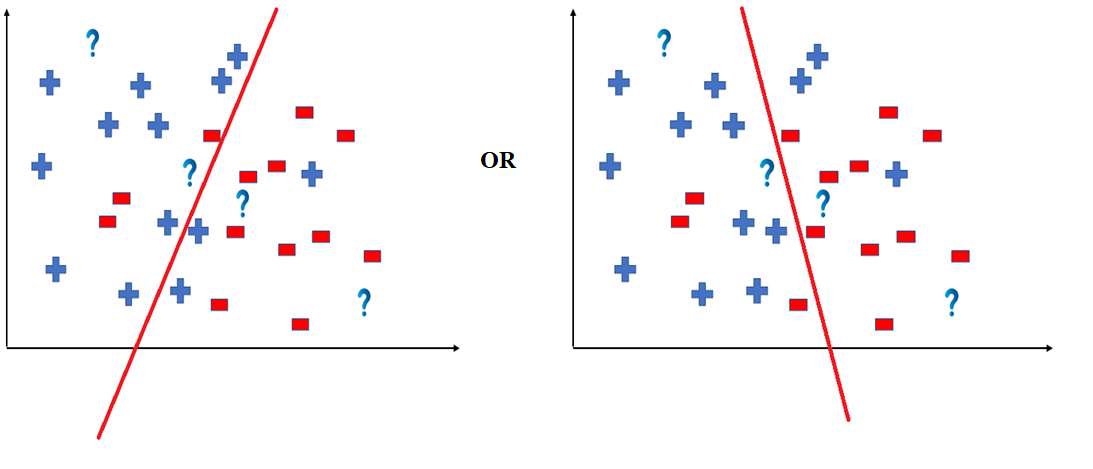
• All these legal possible ways in which we can divide the coordinate plane to predict the outcome of the test data composes of the Hypothesis Space.
• Each individual possible way is known as the hypothesis.

Hence, in this example the hypothesis space would be like:

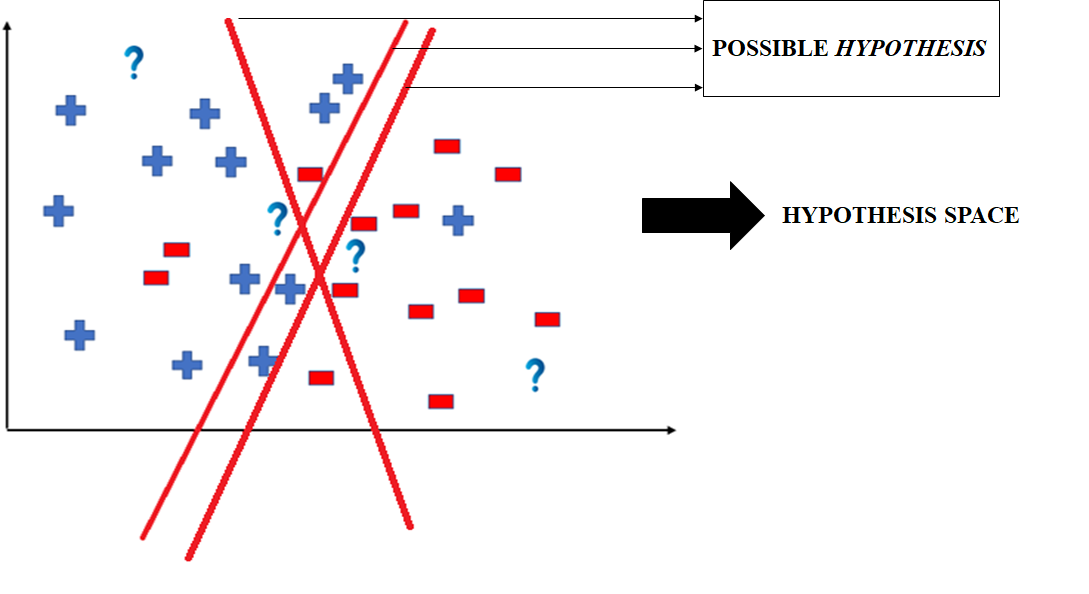
The hypothesis space comprises all possible legal hypotheses that a machine learning algorithm can consider. Hypotheses are formulated based on various algorithms and techniques, including linear regression, decision trees, and neural networks. These hypotheses capture the mapping function transforming input data into predictions.

Hypothesis Formulation and Representation in Machine Learning

Hypotheses in machine learning are formulated based on various algorithms and techniques, each with its representation. For example:

• Linear Regression : [Tex] h(X) = \theta_0 + \theta_1 X_1 + \theta_2 X_2 + … + \theta_n X_n[/Tex]
• Decision Trees : [Tex]h(X) = \text{Tree}(X)[/Tex]
• Neural Networks : [Tex]h(X) = \text{NN}(X)[/Tex]

In the case of complex models like neural networks, the hypothesis may involve multiple layers of interconnected nodes, each performing a specific computation.

Hypothesis Evaluation:

The process of machine learning involves not only formulating hypotheses but also evaluating their performance. This evaluation is typically done using a loss function or an evaluation metric that quantifies the disparity between predicted outputs and ground truth labels. Common evaluation metrics include mean squared error (MSE), accuracy, precision, recall, F1-score, and others. By comparing the predictions of the hypothesis with the actual outcomes on a validation or test dataset, one can assess the effectiveness of the model.

Hypothesis Testing and Generalization:

Once a hypothesis is formulated and evaluated, the next step is to test its generalization capabilities. Generalization refers to the ability of a model to make accurate predictions on unseen data. A hypothesis that performs well on the training dataset but fails to generalize to new instances is said to suffer from overfitting. Conversely, a hypothesis that generalizes well to unseen data is deemed robust and reliable.

The process of hypothesis formulation, evaluation, testing, and generalization is often iterative in nature. It involves refining the hypothesis based on insights gained from model performance, feature importance, and domain knowledge. Techniques such as hyperparameter tuning, feature engineering, and model selection play a crucial role in this iterative refinement process.

In statistics , a hypothesis refers to a statement or assumption about a population parameter. It is a proposition or educated guess that helps guide statistical analyses. There are two types of hypotheses: the null hypothesis (H0) and the alternative hypothesis (H1 or Ha).

• Null Hypothesis(H 0 ): This hypothesis suggests that there is no significant difference or effect, and any observed results are due to chance. It often represents the status quo or a baseline assumption.
• Aternative Hypothesis(H 1 or H a ): This hypothesis contradicts the null hypothesis, proposing that there is a significant difference or effect in the population. It is what researchers aim to support with evidence.

Q. How does the training process use the hypothesis?

The learning algorithm uses the hypothesis as a guide to minimise the discrepancy between expected and actual outputs by adjusting its parameters during training.

Q. How is the hypothesis’s accuracy assessed?

Usually, a cost function that calculates the difference between expected and actual values is used to assess accuracy. Optimising the model to reduce this expense is the aim.

Q. What is Hypothesis testing?

Hypothesis testing is a statistical method for determining whether or not a hypothesis is correct. The hypothesis can be about two variables in a dataset, about an association between two groups, or about a situation.

Q. What distinguishes the null hypothesis from the alternative hypothesis in machine learning experiments?

The null hypothesis (H0) assumes no significant effect, while the alternative hypothesis (H1 or Ha) contradicts H0, suggesting a meaningful impact. Statistical testing is employed to decide between these hypotheses.

Similar Reads

Please login to comment..., improve your coding skills with practice.

What kind of Experience do you want to share?

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, chi-square test, what is hypothesis testing in statistics types and examples, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, mean squared error: overview, examples, concepts and more, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution, all you need to know about bias in statistics, a complete guide to get a grasp of time series analysis.

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, hypothesis testing in statistics - types | examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world, decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis and hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

The Ultimate Ticket to Top Data Science Job Roles

Importance of Hypothesis Testing in Data Analysis

Here is what makes hypothesis testing so important in data analysis and why it is key to making better decisions:

Avoiding Misleading Conclusions (Type I and Type II Errors)

One of the biggest benefits of hypothesis testing is that it helps you avoid jumping to the wrong conclusions. For instance, a Type I error could occur if a company launches a new product thinking it will be a hit, only to find out later that the data misled them. A Type II error might happen when a company overlooks a potentially successful product because their testing wasn’t thorough enough. By setting up the right significance level and carefully calculating the p-value, hypothesis testing minimizes the chances of these errors, leading to more accurate results.

Making Smarter Choices

Hypothesis testing is key to making smarter, evidence-based decisions. Let’s say a city planner wants to determine if building a new park will increase community engagement. By testing the hypothesis using data from similar projects, they can make an informed choice. Similarly, a teacher might use hypothesis testing to see if a new teaching method actually improves student performance. It’s about taking the guesswork out of decisions and relying on solid evidence instead.

Optimizing Business Tactics

In business, hypothesis testing is invaluable for testing new ideas and strategies before fully committing to them. For example, an e-commerce company might want to test whether offering free shipping increases sales. By using hypothesis testing, they can compare sales data from customers who received free shipping offers and those who didn’t. This allows them to base their business decisions on data, not hunches, reducing the risk of costly mistakes.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternative Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps in Hypothesis Testing

Hypothesis testing is a statistical method to determine if there is enough evidence in a sample of data to infer that a certain condition is true for the entire population. Here’s a breakdown of the typical steps involved in hypothesis testing:

Formulate Hypotheses

• Null Hypothesis (H0): This hypothesis states that there is no effect or difference, and it is the hypothesis you attempt to reject with your test.
• Alternative Hypothesis (H1 or Ha): This hypothesis is what you might believe to be true or hope to prove true. It is usually considered the opposite of the null hypothesis.

Choose the Significance Level (α)

The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. Common choices for α are 0.05 (5%), 0.01 (1%), and 0.10 (10%).

Select the Appropriate Test

Choose a statistical test based on the type of data and the hypothesis. Common tests include t-tests, chi-square tests, ANOVA, and regression analysis. The selection depends on data type, distribution, sample size, and whether the hypothesis is one-tailed or two-tailed.

Collect Data

Gather the data that will be analyzed in the test. To infer conclusions accurately, this data should be representative of the population.

Calculate the Test Statistic

Based on the collected data and the chosen test, calculate a test statistic that reflects how much the observed data deviates from the null hypothesis.

Determine the p-value

The p-value is the probability of observing test results at least as extreme as the results observed, assuming the null hypothesis is correct. It helps determine the strength of the evidence against the null hypothesis.

Make a Decision

Compare the p-value to the chosen significance level:

• If the p-value ≤ α: Reject the null hypothesis, suggesting sufficient evidence in the data supports the alternative hypothesis.
• If the p-value > α: Do not reject the null hypothesis, suggesting insufficient evidence to support the alternative hypothesis.

Report the Results

Present the findings from the hypothesis test, including the test statistic, p-value, and the conclusion about the hypotheses.

Perform Post-hoc Analysis (if necessary)

Depending on the results and the study design, further analysis may be needed to explore the data more deeply or to address multiple comparisons if several hypotheses were tested simultaneously.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

3. Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

ANOVA , or Analysis of Variance, is a statistical method used to compare the means of three or more groups. It’s particularly useful when you want to see if there are significant differences between multiple groups. For instance, in business, a company might use ANOVA to analyze whether three different stores are performing differently in terms of sales. It’s also widely used in fields like medical research and social sciences, where comparing group differences can provide valuable insights.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Become a Data Scientist through hands-on learning with hackathons, masterclasses, webinars, and Ask-Me-Anything sessions! Start learning!

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Serious About Success? Don't Settle for Less

Practice Problems on Hypothesis Testing

Here are the practice problems on hypothesis testing that will help you understand how to apply these concepts in real-world scenarios:

A telecom service provider claims that customers spend an average of ₹400 per month, with a standard deviation of ₹25. However, a random sample of 50 customer bills shows a mean of ₹250 and a standard deviation of ₹15. Does this sample data support the service provider’s claim?

Solution: Let’s break this down:

• Null Hypothesis (H0): The average amount spent per month is ₹400.
• Alternate Hypothesis (H1): The average amount spent per month is not ₹400.
• Population Standard Deviation (σ): ₹25
• Sample Size (n): 50
• Sample Mean (x̄): ₹250

1. Calculate the z-value:

z=250-40025/50 −42.42

2. Compare with critical z-values: For a 5% significance level, critical z-values are -1.96 and +1.96. Since -42.42 is far outside this range, we reject the null hypothesis. The sample data suggests that the average amount spent is significantly different from ₹400.

Out of 850 customers, 400 made online grocery purchases. Can we conclude that more than 50% of customers are moving towards online grocery shopping?

Solution: Here’s how to approach it:

• Proportion of customers who shopped online (p): 400 / 850 = 0.47
• Null Hypothesis (H0): The proportion of online shoppers is 50% or more.
• Alternate Hypothesis (H1): The proportion of online shoppers is less than 50%.
• Sample Size (n): 850
• Significance Level (α): 5%

z=p-PP(1-P)/n

z=0.47-0.500.50.5/850  −1.74

2. Compare with the critical z-value: For a 5% significance level (one-tailed test), the critical z-value is -1.645. Since -1.74 is less than -1.645, we reject the null hypothesis. This means the data does not support the idea that most customers are moving towards online grocery shopping.

In a study of code quality, Team A has 250 errors in 1000 lines of code, and Team B has 300 errors in 800 lines of code. Can we say Team B performs worse than Team A?

Solution: Let’s analyze it:

• Proportion of errors for Team A (pA): 250 / 1000 = 0.25
• Proportion of errors for Team B (pB): 300 / 800 = 0.375
• Null Hypothesis (H0): Team B’s error rate is less than or equal to Team A’s.
• Alternate Hypothesis (H1): Team B’s error rate is greater than Team A’s.
• Sample Size for Team A (nA): 1000
• Sample Size for Team B (nB): 800

p=nApA+nBpBnA+nB

p=10000.25+8000.3751000+800 ≈ 0.305

z=​pA−pB​p(1-p)(1nA+1nB)

z=​0.25−0.375​0.305(1-0.305) (11000+1800) ≈ −5.72

2. Compare with the critical z-value: For a 5% significance level (one-tailed test), the critical z-value is +1.645. Since -5.72 is far less than +1.645, we reject the null hypothesis. The data indicates that Team B’s performance is significantly worse than Team A’s.

Our Data Scientist Master's Program will help you master core topics such as R, Python, Machine Learning, Tableau, Hadoop, and Spark. Get started on your journey today!

Applications of Hypothesis Testing

Apart from the practical problems, let's look at the real-world applications of hypothesis testing across various fields:

Medicine and Healthcare

In medicine, hypothesis testing plays a pivotal role in assessing the success of new treatments. For example, researchers may want to find out if a new exercise regimen improves heart health. By comparing data from patients who followed the program to those who didn’t, they can determine if the exercise significantly improves health outcomes. Such rigorous testing allows medical professionals to rely on proven methods rather than assumptions.

Quality Control and Manufacturing

In manufacturing, ensuring product quality is vital, and hypothesis testing helps maintain those standards. Suppose a beverage company introduces a new bottling process and wants to verify if it reduces contamination. By analyzing samples from the new and old processes, hypothesis testing can reveal whether the new method reduces the risk of contamination. This allows manufacturers to implement improvements that enhance product safety and quality confidently.

Education and Learning

In education and learning, hypothesis testing is a tool to evaluate the impact of innovative teaching techniques. Imagine a situation where teachers introduce project-based learning to boost critical thinking skills. By comparing the performance of students who engaged in project-based learning with those in traditional settings, educators can test their hypothesis. The results can help educators make informed choices about adopting new teaching strategies.

Environmental Science

Hypothesis testing is essential in environmental science for evaluating the effectiveness of conservation measures. For example, scientists might explore whether a new water management strategy improves river health. By collecting and comparing data on water quality before and after the implementation of the strategy, they can determine whether the intervention leads to positive changes. Such findings are crucial for guiding environmental decisions that have long-term impacts.

Marketing and Advertising

In marketing, businesses use hypothesis testing to refine their approaches. For instance, a clothing brand might test if offering limited-time discounts increases customer loyalty. By running campaigns with and without the discount and analyzing the outcomes, they can assess if the strategy boosts customer retention. Data-driven insights from hypothesis testing enable companies to design marketing strategies that resonate with their audience and drive growth.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

Learn All The Tricks Of The BI Trade

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore the Post Graduate Program in Data Science.

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is H0 and H1 in statistics?

In statistics, H0​ and H1​ represent the null and alternative hypotheses. The null hypothesis, H0​, is the default assumption that no effect or difference exists between groups or conditions. The alternative hypothesis, H1​, is the competing claim suggesting an effect or a difference. Statistical tests determine whether to reject the null hypothesis in favor of the alternative hypothesis based on the data.

3. What is a simple hypothesis with an example?

A simple hypothesis is a specific statement predicting a single relationship between two variables. It posits a direct and uncomplicated outcome. For example, a simple hypothesis might state, "Increased sunlight exposure increases the growth rate of sunflowers." Here, the hypothesis suggests a direct relationship between the amount of sunlight (independent variable) and the growth rate of sunflowers (dependent variable), with no additional variables considered.

4. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

5. What software tools can assist with hypothesis testing?

Several software tools offering distinct features can help with hypothesis testing. R and RStudio are popular for their advanced statistical capabilities. The Python ecosystem, including libraries like SciPy and Statsmodels, also supports hypothesis testing. SAS and SPSS are well-established tools for comprehensive statistical analysis. For basic testing, Excel offers simple built-in functions.

6. How do I interpret the results of a hypothesis test?

Interpreting hypothesis test results involves comparing the p-value to the significance level (alpha). If the p-value is less than or equal to alpha, you can reject the null hypothesis, indicating statistical significance. This suggests that the observed effect is unlikely to have occurred by chance, validating your analysis findings.

7. Why is sample size important in hypothesis testing?

Sample size is crucial in hypothesis testing as it affects the test’s power. A larger sample size increases the likelihood of detecting a true effect, reducing the risk of Type II errors. Conversely, a small sample may lack the statistical power needed to identify differences, potentially leading to inaccurate conclusions.

8. Can hypothesis testing be used for non-numerical data?

Yes, hypothesis testing can be applied to non-numerical data through non-parametric tests. These tests are ideal when data doesn't meet parametric assumptions or when dealing with categorical data. Non-parametric tests, like the Chi-square or Mann-Whitney U test, provide robust methods for analyzing non-numerical data and drawing meaningful conclusions.

9. How do I choose the proper hypothesis test?

Selecting the right hypothesis test depends on several factors: the objective of your analysis, the type of data (numerical or categorical), and the sample size. Consider whether you're comparing means, proportions, or associations, and whether your data follows a normal distribution. The correct choice ensures accurate results tailored to your research question.

Find our PL-300 Microsoft Power BI Certification Training Online Classroom training classes in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Top 10 Automation Tools to Secure Your Career Growth in 2025

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, OPM3 and the PMI ATP seal are the registered marks of the Project Management Institute, Inc.