
When Do You Reject the Null Hypothesis? (3 Examples)
A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.
We always use the following steps to perform a hypothesis test:
Step 1: State the null and alternative hypotheses.
The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.
The alternative hypothesis , denoted as H A , is the hypothesis that the sample data is influenced by some non-random cause.
2. Determine a significance level to use.
Decide on a significance level. Common choices are .01, .05, and .1.
3. Calculate the test statistic and p-value.
Use the sample data to calculate a test statistic and a corresponding p-value .
4. Reject or fail to reject the null hypothesis.
If the p-value is less than the significance level, then you reject the null hypothesis.
If the p-value is not less than the significance level, then you fail to reject the null hypothesis.
You can use the following clever line to remember this rule:
“If the p is low, the null must go.”
In other words, if the p-value is low enough then we must reject the null hypothesis.
The following examples show when to reject (or fail to reject) the null hypothesis for the most common types of hypothesis tests.
Example 1: One Sample t-test
A one sample t-test is used to test whether or not the mean of a population is equal to some value.
For example, suppose we want to know whether or not the mean weight of a certain species of turtle is equal to 310 pounds.
We go out and collect a simple random sample of 40 turtles with the following information:
- Sample size n = 40
- Sample mean weight x = 300
- Sample standard deviation s = 18.5
We can use the following steps to perform a one sample t-test:
Step 1: State the Null and Alternative Hypotheses
We will perform the one sample t-test with the following hypotheses:
- H 0 : μ = 310 (population mean is equal to 310 pounds)
- H A : μ ≠ 310 (population mean is not equal to 310 pounds)
We will choose to use a significance level of 0.05 .
We can plug in the numbers for the sample size, sample mean, and sample standard deviation into this One Sample t-test Calculator to calculate the test statistic and p-value:
- t test statistic: -3.4187
- two-tailed p-value: 0.0015
Since the p-value (0.0015) is less than the significance level (0.05) we reject the null hypothesis .
We conclude that there is sufficient evidence to say that the mean weight of turtles in this population is not equal to 310 pounds.
Example 2: Two Sample t-test
A two sample t-test is used to test whether or not two population means are equal.
For example, suppose we want to know whether or not the mean weight between two different species of turtles is equal.
We go out and collect a simple random sample from each population with the following information:
- Sample size n 1 = 40
- Sample mean weight x 1 = 300
- Sample standard deviation s 1 = 18.5
- Sample size n 2 = 38
- Sample mean weight x 2 = 305
- Sample standard deviation s 2 = 16.7
We can use the following steps to perform a two sample t-test:
We will perform the two sample t-test with the following hypotheses:
- H 0 : μ 1 = μ 2 (the two population means are equal)
- H 1 : μ 1 ≠ μ 2 (the two population means are not equal)
We will choose to use a significance level of 0.10 .
We can plug in the numbers for the sample sizes, sample means, and sample standard deviations into this Two Sample t-test Calculator to calculate the test statistic and p-value:
- t test statistic: -1.2508
- two-tailed p-value: 0.2149
Since the p-value (0.2149) is not less than the significance level (0.10) we fail to reject the null hypothesis .
We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.
Example 3: Paired Samples t-test
A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.
For example, suppose we want to know whether or not a certain training program is able to increase the max vertical jump of college basketball players.
To test this, we may recruit a simple random sample of 20 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month:

We can use the following steps to perform a paired samples t-test:
We will perform the paired samples t-test with the following hypotheses:
- H 0 : μ before = μ after (the two population means are equal)
- H 1 : μ before ≠ μ after (the two population means are not equal)
We will choose to use a significance level of 0.01 .
We can plug in the raw data for each sample into this Paired Samples t-test Calculator to calculate the test statistic and p-value:
- t test statistic: -3.226
- two-tailed p-value: 0.0045
Since the p-value (0.0045) is less than the significance level (0.01) we reject the null hypothesis .
We have sufficient evidence to say that the mean vertical jump before and after participating in the training program is not equal.
Bonus: Decision Rule Calculator
You can use this decision rule calculator to automatically determine whether you should reject or fail to reject a null hypothesis for a hypothesis test based on the value of the test statistic.
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
What is The Null Hypothesis & When Do You Reject The Null Hypothesis
Julia Simkus
Editor at Simply Psychology
BA (Hons) Psychology, Princeton University
Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.
Learn about our Editorial Process
Saul McLeod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.
The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).
The null hypothesis is the statement that a researcher or an investigator wants to disprove.
Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.
How to Write a Null Hypothesis
Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.
It is a default position that your research aims to challenge or confirm.
For example, if studying the impact of exercise on weight loss, your null hypothesis might be:
There is no significant difference in weight loss between individuals who exercise daily and those who do not.
Examples of Null Hypotheses
| Research Question | Null Hypothesis |
|---|---|
| Do teenagers use cell phones more than adults? | Teenagers and adults use cell phones the same amount. |
| Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil? | Tomato plants show no difference in growth rates when planted in compost rather than soil. |
| Does daily meditation decrease the incidence of depression? | Daily meditation does not decrease the incidence of depression. |
| Does daily exercise increase test performance? | There is no relationship between daily exercise time and test performance. |
| Does the new vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does flossing your teeth affect the number of cavities? | Flossing your teeth has no effect on the number of cavities. |
When Do We Reject The Null Hypothesis?
We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.
If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.
Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).
If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.
You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.
Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.
The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.
When your p-value is less than or equal to your significance level, you reject the null hypothesis.
In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.
In this case, the sample data provides insufficient data to conclude that the effect exists in the population.
Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.
When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.
Why Do We Never Accept The Null Hypothesis?
The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.
A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.
It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.
One can either reject the null hypothesis, or fail to reject it, but can never accept it.
Why Do We Use The Null Hypothesis?
We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.
The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).
A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.
Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.
Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.
It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.
Purpose of a Null Hypothesis
- The primary purpose of the null hypothesis is to disprove an assumption.
- Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
- A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.
Do you always need both a Null Hypothesis and an Alternative Hypothesis?
The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.
While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.
The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.
What is the difference between a null hypothesis and an alternative hypothesis?
The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.
It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.
What are some problems with the null hypothesis?
One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.
Why can a null hypothesis not be accepted?
We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.
We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.
Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.
If the p-value is greater than the significance level, then you fail to reject the null hypothesis.
Is a null hypothesis directional or non-directional?
A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.
A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.
A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.
The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.
Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.
Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.
Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.
Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.
Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
Hypothesis Testing (cont...)
Hypothesis testing, the null and alternative hypothesis.
In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.
The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:
| Null Hypotheses (H ): | Undertaking seminar classes has no effect on students' performance. |
| Alternative Hypothesis (H ): | Undertaking seminar class has a positive effect on students' performance. |
Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:
| Null Hypotheses (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is the same in the population. |
| Alternative Hypothesis (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is not the same in the population. |
Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.

Significance levels
The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?
So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.
Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions
When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:
| Alternative Hypothesis (H ): | Undertaking seminar classes has a positive effect on students' performance. |
The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.
Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.
Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:
| Alternative Hypothesis (H ): | Undertaking seminar classes has an effect on students' performance. |
In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.
Rejecting or failing to reject the null hypothesis
Let's return finally to the question of whether we reject or fail to reject the null hypothesis.
If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Prevent plagiarism. Run a free check.
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved October 19, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.
Support or Reject the Null Hypothesis in Easy Steps
- What does it mean to support ot reject the null hypothesis?
- General Situations: P Value
- P Value Guidelines
- A Proportion
- A Proportion (second example)
What does it mean to support or reject the null hypothesis?
In many statistical tests, the main goal is to either support or reject the null hypothesi s. This means that we’re either going to keep the original hypothesis in place, or we’re not. For example, if your null hypothesis is that grass grows more than one inch per day, but an experiment shows it grows less than one inch per day, then you can throw out (reject) the null hypothesis.
For new statistics students, the term can be a tricky term to grasp, partly because the name “null hypothesis” doesn’t make it clear about what the null hypothesis actually is!
So, what exactly is the null hypothesis? You can think of it as a hypothesis that can be nullified or dismissed . If you reject the null hypothesis, it is replaced with the alternate hypothesis , which is what you suspect might be the actual truth about a particular situation.
Let’s illustrate this with a real-life example. In the 1990s, researchers suspected that Fen-Phen, a “miracle” weight loss drug was linked to a recent surge in serious lung problems. American Home Products Corporation, who marketed the drug, believed it was safe.
- The null hypothesis is always the accepted hypothesis; in this scenario, the drug was on the market, people were taking it, and it was widely accepted as a safe drug for weight loss. Thus, the null hypothesis was that the drug is safe.
- The alternate hypothesis suggested that the drug wasn’t safe.
After some analysis by researchers, the null hypothesis that Fen-Phen was safe was rejected, and the drug was subsequently withdrawn from the market.
Support or Reject the Null Hypothesis: General steps
- State the null hypothesis. When you state the null hypothesis , you also have to state the alternate hypothesis . Sometimes it is easier to state the alternate hypothesis first, because that’s the researcher’s thoughts about the experiment.
- Support or reject the null hypothesis . You reject the null hypothesis when your test value falls into the rejection region .
- If you are able to reject the null hypothesis in Step 2, you can replace it with the alternate hypothesis.
The exact method you follow depends mainly on if you have a proportion or a p-value :
- P Value Instructions
- Proportion Instructions
Support or Reject Null Hypothesis with a P Value
If you have a P-value , or are asked to find a p-value, follow these instructions to support or reject the null hypothesis. This method works if you are given an alpha level and if you are not given an alpha level. If you are given a confidence level , subtract from 1 to get the alpha level.
- State the null hypothesis and the alternate hypothesis (“the claim”). If you aren’t sure how to do this, follow this link for How To State the Null and Alternate Hypothesis .
- Find the critical value . When beginning statistics, you usually deal with a normally distributed population, so the critical value will be found with a z-score . Use the following formula to find the z-score .
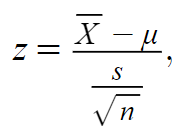
- Compare your answer from step 4 with the α value given in the question. If step 4 is less than or equal to α, reject the null hypothesis, otherwise do not reject it.
What p-value fails to reject the null hypothesis?
If the p-value is greater than the significance level, we usually do not reject the null hypothesis. A large p-value indicates that the data is not significant , so we cannot conclude that the null hypothesis is false. For example, if we set the significance level at 0.05 and the p-value is 0.10, then the p-value is larger than 0.05 and we would fail to reject the null hypothesis.
However, failing to reject the null hypothesis does not imply that the alternate hypothesis is true. It just means that the data does not provide sufficient evidence to conclude it is false.
To increase the certainty of rejecting the null hypothesis, choose a lower significance level. For example, setting the significance level to 0.01 would require the p-value to be less than or equal to 0.01 to reject the null hypothesis.
Refer to this rule of thumb to decide if you should support or reject the null hypothesis (the more “significant,” the more reason to reject the null):
- If p value > .10 → “not significant”
- If p value ≤ .10 → “marginally significant”
- If p value ≤ .05 → “significant”
- If p value ≤ .01 → “highly significant.”
Back to Top
Support or Reject Null Hypothesis for a Proportion
Sometimes, you’ll be given a proportion of the population or a percentage and asked to support or reject null hypothesis. In this case you can’t compute a test value by calculating a z-score (you need actual numbers for that), so we use a slightly different technique.
Example question 1: A researcher claims that Democrats will win the next election. 4300 voters were polled; 2200 said they would vote Democrat. Decide if you should support or reject null hypothesis. Is there enough evidence at α=0.05 to support this claim?
- State the null hypothesis and the alternate hypothesis (“the claim”). H o :p ≤ 0.5 H 1 :p > .5
- Look up Step 3 in the z-table to get .9418.
- Calculate your p-value by subtracting Step 4 from 1. 1-.9418 = .0582
- Compare your answer from step 5 with the α value given in the question. Support or reject the null hypothesis? If step 5 is less than α, reject the null hypothesis, otherwise do not reject it. In this case, .582 (5.82%) is not less than our α, so we do not reject the null hypothesis.
Example question 2: A researcher claims that more than 23% of community members go to church regularly. In a recent survey, 126 out of 420 people stated they went to church regularly. Is there enough evidence at α = 0.05 to support this claim? Use the P-Value method to support or reject null hypothesis.
- State the null hypothesis and the alternate hypothesis (“the claim”). H o :p ≤ 0.23; H 1 :p > 0.23 (claim).
- Find ‘p’ by converting the stated claim to a decimal: 23% = 0.23. Also, find ‘q’ by subtracting ‘p’ from 1: 1 – 0.23 = 0.77.
- Use the following formula to calculate your test value.
- Multiply p and q together, then divide by the number in the random sample. (0.23 x 0.77) / 420 = 0.00042
- Take the square root of your answer to 2. √(0.1771) = 0.0205
- Divide your answer to 1. by your answer in 3. 0.07 / 0.0205 = 3.41
- Find the P-Value by looking up your answer from step 5 in the z-table . The z-score for 3.41 is .4997. Subtract from 0.500: 0.500-.4997 = 0.003.
- Compare your P-value to α. If the P-value is less, reject the null hypothesis. If the P-value is more, keep the null hypothesis. 0.003 < 0.05, so we have enough evidence to reject the null hypothesis and accept the claim.
Note: In Step 5, I’m using the z-table on this site to solve this problem. Most textbooks have the right of z-table . If you’re seeing .9997 as an answer in your textbook table, then your textbook has a “whole z” table, in which case don’t subtract from .5, subtract from 1. 1-.9997 = 0.003.
Check out our Youtube channel for video tips!
How do you know when to reject the null hypothesis?
To determine whether or not to reject the null hypothesis, two common criteria are typically considered:
- Significance (alpha) level: The significance level represents the probability of committing a Type I error , which involves mistakenly rejecting the null hypothesis when it is actually true. The most commonly used significance level is 0.05, implying a willingness to accept a 5% chance of committing a Type I error.
- Power : Power refers to the probability of correctly rejecting the null hypothesis when it is false. Higher power indicates a greater likelihood of rejecting the null hypothesis when it is false, thereby reducing the probability of a Type II error.
In a nutshell, the null hypothesis can be rejected if the test results are statistically significant , which means that they are unlikely to have happened by chance. This determination can be made by comparing the p-value of the results with the significance level.
However, even when the results are significant, exercise caution if the power is low. This is because low power increases the likelihood of committing a Type I error. Therefore, in real life studies, you should ideally take into account both the significance level and power when deciding whether or not to reject the null hypothesis.
Other factors can to take into account:
- Effect size: Larger effect sizes are more likely to lead to rejecting the null hypothesis.
- Consequences of a Type I error : If there is a high cost associated with making a Type I error, it may be prudent to be more conservative and not reject the null hypothesis, even when the results are significant. For example, if a drug trial incorrectly indicates that a drug is safe, the drug may be prescribed to patients — even though it may be harmful.
- Consequences of a Type II error : If the cost of making a Type II error is high, it may be more appropriate to reject the null hypothesis, even if the power is low. For example, if a medical test incorrectly indicates a patient doesn’t have a disease, they may miss out on life-saving treatment.
What is the difference between failing to reject the null hypothesis and having evidence to support the alternate hypothesis?
Not rejecting the null hypothesis and having evidence for the alternative hypothesis are two entirely different concepts.
Not rejecting the null hypothesis signifies that the data does not provide sufficient evidence to conclude that the null hypothesis is false. The data may, or may not, align with either of the hypotheses.
Having evidence to support the alternative hypothesis indicates that the data offers some indication that the null hypothesis is false. However, it is important to note that evidence is not equivalent to proof. Merely having evidence for the alternative hypothesis does not guarantee its validity. And although I’m saying “support the alternate hypothesis” here to illustrate the point, statistical tests don’t actually provide support for the alternate hypotheses; instead, they provide evidence to throw out the null (and put the alternate in its place).
- Authors of the study: Lucia Bandiera, Geethanjali Pavar, Gabriele Pisetta, Shuji Otomo, Enzo Mangano, Jonathan R. Seckl, Paul Digard, Emanuela Molinari, Filippo Menolascina and Ignazio Maria Viola, CC BY 4.0 , via Wikimedia Commons

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

9.1: Null and Alternative Hypotheses
- Last updated
- Save as PDF
- Page ID 23459

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.
| equal (=) | not equal \((\neq)\) greater than (>) less than (<) |
| greater than or equal to \((\geq)\) | less than (<) |
| less than or equal to \((\geq)\) | more than (>) |
\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example \(\PageIndex{1}\)
- \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
- \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)
Exercise \(\PageIndex{1}\)
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
- \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
- \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)
Example \(\PageIndex{2}\)
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
- \(H_{0}: \mu = 2.0\)
- \(H_{a}: \mu \neq 2.0\)
Exercise \(\PageIndex{2}\)
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.
- \(H_{0}: \mu \_ 66\)
- \(H_{a}: \mu \_ 66\)
- \(H_{0}: \mu = 66\)
- \(H_{a}: \mu \neq 66\)
Example \(\PageIndex{3}\)
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
- \(H_{0}: \mu \geq 5\)
- \(H_{a}: \mu < 5\)
Exercise \(\PageIndex{3}\)
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- \(H_{0}: \mu \_ 45\)
- \(H_{a}: \mu \_ 45\)
- \(H_{0}: \mu \geq 45\)
- \(H_{a}: \mu < 45\)
Example \(\PageIndex{4}\)
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
- \(H_{0}: p \leq 0.066\)
- \(H_{a}: p > 0.066\)
Exercise \(\PageIndex{4}\)
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.
- \(H_{0}: p \_ 0.40\)
- \(H_{a}: p \_ 0.40\)
- \(H_{0}: p = 0.40\)
- \(H_{a}: p > 0.40\)
COLLABORATIVE EXERCISE
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:
- Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
- Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
- If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
- Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.
Formula Review
\(H_{0}\) and \(H_{a}\) are contradictory.
| equal \((=)\) | greater than or equal to \((\geq)\) | less than or equal to \((\leq)\) | |
| has: | not equal \((\neq)\) greater than \((>)\) less than \((<)\) | less than \((<)\) | greater than \((>)\) |
- If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
- If\(\alpha > p\)-value, then reject \(H_{0}\).
\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References
Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
5.1 - hypothesis testing overview.
Jin asked Carlos if he had taken statistics, Carlos said he had but it was a long time ago and he did not remember a lot of it. Jin told Carlos understanding hypothesis testing would help him understand what the judge just said. In most research, a researcher has a “research hypothesis”, that is, what the research THINKS is going to occur because of some kind of intervention or treatment. In the courtroom the prosecutor is the researcher, thinking the person on trial is guilty. This would be the research hypothesis; guilty. However, as most of us know, the U.S. legal system operates that a person is innocent until PROVEN guilty. In other words, we have to believe innocence until there is enough evidence to change our mind that the person on trial is actually not innocent. In hypothesis testing, we refer to the presumption of innocence as the NULL HYPOTHESIS. So while the prosecutor has a research hypothesis, it must be shown that the presumption of innocence can be rejected.
Like the judge in the TV show, if we have enough evidence to conclude that the null is not true, we can reject the null. Jin explained that if the judge had enough evidence to conclude the person on trial was not innocent she would have. The judge specifically stated that she did not have enough evidence to reject innocence (the null hypothesis).
When the judge acquits a defendant, as on the T.V. show, this does not mean that the judge accepts the defendant’s claim of innocence. It only says that innocence is plausible because guilt has not been established beyond a reasonable doubt.
On the other hand, if the judge returns a guilty verdict she has concluded innocence (null) is not plausible given the evidence presented, therefore she rejects the statute of the null, innocence and concludes the alternative hypothesis- guilty .
Let’s take a closer look at how this works.
Making a Decision Section
Taking a sample of 500 Penn State students, we asked them if they like cold weather, we observe a sample proportion of 0.556, since these students go to school in Pennsylvania it might generally be thought the true proportion of students who like cold weather is 0.5, in other words the NULL hypothesis is that the true population proportion equal to 0.5 ,
In order to “test” what is generally thought about these students (half of them like cold weather) we have to ask about the relationship of the data we have (from our sample) relative to the hypothesized null value. In other words, is our observed sample proportion far enough away from the 0.5 to suggest that there is evidence against the null? Translating this to statistical terms, we can think about the “how far” questions in terms of standard deviations. How many standard deviations apart would we consider to be “meaningfully different”?
What if instead of a cutoff standard deviation, we found a probability? With a null hypothesis of equal to 0.5, the alternative hypothesis is not equal to 0.50. To test this, we convert the distance between the observed value and the null value into a standardized statistic. We have worked with standardized scores when working with z scores. We also learned about the empirical rule. Combining these two concepts, we can begin to make decisions about “how far” the observed value and null hypothesis need to be to be “meaningfully different”.
To do this we calculate a Z statistic, which is a standardized score of the difference.
\(z^{*}=\dfrac{\hat{p}-p_{0}}{\sqrt{\frac{p_{0}\left(1-p_{0}\right)}{n}}}\)
We can look at the results of calculating a z test (which we will do using software). Large test statistics indicate a large difference between the observed value and the null, contributing to greater evidence of a significant difference, thus casting doubt that the true population proportion is the null value.
Accompanying the magnitude of the test statistic, our software also yields a “probability”. Returning to the values of the empirical rule we know the percentiles under a standard normal curve. We can apply these to determine the probability (which is really a percentile) of getting an observed score IF the null hypothesis is indeed true (or the mean of the distribution). In this class, we will not be calculating these by hand, but we do need to understand what the “p-values'' in the output mean. In our example, after calculating a z statistic, we determine that if the true proportion is 0.5, the probability we would get a sample proportion of 0.556 is 0.0061. This is a very small probability as measure against the standard defining “small” as a probability less than .05. In this case, we would reject the null hypothesis as a probable value for the population based on the evidence from our sample.
While p values are a standard in most statistics courses and textbook there have been recent conversations about the use of p values.
American Statistical Association Releases Statement on Statistical Significance and P-Values
The use of p-values is a common practice in statistical inference but also not without its controversy. In March of 2016, the American Statistical Association released a statement regarding p-values and their use in statistical studies and decision making.
You can review the full article: ASA Statement on p-Values: Context, Process and Purpose
P-Values Section
Before we proceed any further we need to step away from the jargon and understand exactly what the heck a p value is. Simply a p value is the probability of getting the observed sample statistic, given the null hypothesis is true . In our example, IF the true proportion of Penn State students who like the cold IS really .5 (as we state in the null hypothesis), what is the probability that we would get an observed sample statistic of .556?
When the probability is small we have one of two options. We can either conclude there is something wrong with our sample (however, if we followed good sampling techniques as discussed early in the notes then this is not likely) OR we can conclude that the null is probably not the true population value.
To summarize the application of the p value:
- If our p-value is less than or equal to \(\alpha \), then there is enough evidence to reject the null hypothesis (in most cases the alpha is going to be 0.05).
- If our p-value is greater than \(\alpha \), there is not enough evidence to reject the null hypothesis.
One should be aware that \(\alpha \) is also called level of significance. This makes for a confusion in terminology. \(\alpha \) is the preset level of significance whereas the p-value is the observed level of significance. The p-value, in fact, is a summary statistic which translates the observed test statistic's value to a probability which is easy to interpret.
We can summarize the data by reporting the p-value and let the users decide to reject \(H_0 \) or not to reject \(H_0 \) for their subjectively chosen \(\alpha\) values.

IMAGES
VIDEO
COMMENTS
If the p-value is not less than the significance level, then you fail to reject the null hypothesis. You can use the following clever line to remember this rule: “If the p is low, the null must go.” In other words, if the p-value is low enough then we must reject the null hypothesis.
A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population.
If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative ...
Decide whether to reject or fail to reject your null hypothesis. Present the findings in your results and discussion section. Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
An hypothesis test is a statistical decision; the conclusion will either be to reject the null hypothesis in favor of the alternative, or to fail to reject the null hypothesis. The decision that we make must, of course, be based on the observed value x of the data vector X.
You reject the null hypothesis when your test value falls into the rejection region. If you are able to reject the null hypothesis in Step 2, you can replace it with the alternate hypothesis. The exact method you follow depends mainly on if you have a proportion or a p-value: P Value Instructions; Proportion Instructions; Support or Reject Null ...
When doing hypothesis testing, two types of mistakes may be made and we call them Type I error and Type II error. If we reject the null hypothesis when it is true, then we made a type I error. If the null hypothesis is false and we failed to reject it, we made another error called a Type II error.
There are two options for a decision. They are "reject \ (H_0\)" if the sample information favors the alternative hypothesis or "do not reject \ (H_0\)" or "decline to reject \ (H_0\)" if the sample information is insufficient to reject the null hypothesis.
In hypothesis testing, we refer to the presumption of innocence as the NULL HYPOTHESIS. So while the prosecutor has a research hypothesis, it must be shown that the presumption of innocence can be rejected.