research hypothesis testing formula

Hypothesis Testing: A Complete Guide for Beginners

Statistical hypothesis testing is a key concept in statistics. It helps researchers, data analysts, and scientists make decisions based on data. Hypothesis testing allows you to determine whether your results are meaningful when analyzing experiments, surveys, or other data.

In this blog, we’ll explain statistical hypothesis testing from the basics to more advanced ideas, making it easy to understand even for 10th-grade students.

By the end of this blog, you’ll be able to understand hypothesis testing and how it’s used in research.

What is a Hypothesis?

Table of Contents

A hypothesis is a statement that can be tested. It’s like a guess you make after observing something, and you want to see if that guess holds when you collect more data.

For example:

• “Eating more vegetables improves health.”
• “Students who study regularly perform better in exams.”

These statements are testable because we can gather data to check if they are true or false.

What is Hypothesis Testing?

Hypothesis testing is a statistical process that helps us make decisions based on data. Suppose you collect data from an experiment or survey. Hypothesis testing helps you decide whether the results are significant or could have happened by chance.

For example, if you believe a new teaching method helps students score better, hypothesis testing can help you decide if the improvement is real or just a random fluctuation.

Null and Alternative Hypothesis

Hypothesis testing usually involves two competing hypotheses:

• Example: “There is no difference in exam scores between students using the new method and those who don’t.”
• Example: “Students using the new method perform better in exams than those who don’t.”

Key Terms in Hypothesis Testing

Before diving into the details, let’s understand some important terms used in hypothesis testing:

1. Test Statistic

The test statistic is a number calculated from your data that is compared against a known distribution (like the normal distribution) to test the null hypothesis. It tells you how much your sample data differs from what’s expected under the null hypothesis.

The p-value is the probability of observing the sample data or something more extreme, assuming the null hypothesis is true. A smaller p-value suggests that the null hypothesis is less likely to be true. In many studies, a p-value of 0.05 or less is considered statistically significant.

3. Significance Level (α)

The significance level is the threshold at which you decide to reject the null hypothesis. Commonly, this level is set at 5% (α = 0.05), meaning there’s a 5% chance of rejecting the null hypothesis even when it is true.

4. Critical Value

The critical value is the boundary that defines the region where we reject the null hypothesis. It is calculated based on the significance level and tells us how extreme the test statistic needs to be to reject the null hypothesis.

5. Type I and Type II Errors

• Type I Error (False Positive): Rejecting the null hypothesis when it’s true.
• Type II Error (False Negative): Failing to reject the null hypothesis when it’s false.

In simpler terms:

• Type I error is like thinking something has changed when it hasn’t.
• Type II error is like thinking nothing has changed when it actually has.

Types of Hypothesis Testing

1. one-tailed test.

A one-tailed test checks for an effect in a single direction. For example, if you are only interested in testing whether students who study 2 hours daily score higher than those who don’t, that’s a one-tailed test.

2. Two-Tailed Test

A two-tailed test checks for an effect in both directions. This means you’re testing if the scores are different , regardless of whether they are higher or lower. For example, “Do students who study 2 hours daily score differently than those who don’t?” That’s a two-tailed test.

Steps in Hypothesis Testing

Step 1: define hypotheses.

Start by defining the:

• Null Hypothesis (H₀): The status quo or no change.
• Alternative Hypothesis (H₁): The hypothesis you believe in, suggesting that something has changed.

Step 2: Set the Significance Level (α)

Next, set the significance level, typically 0.05 . This means you’re willing to accept a 5% risk of incorrectly rejecting the null hypothesis.

Step 3: Collect and Analyze Data

Conduct your experiment or survey and collect data. Then, analyze this data to calculate the test statistic. The formula you use depends on the type of test you’re conducting (e.g., Z-test, T-test).

Step 4: Calculate the P-value or Critical Value

Compare the test statistic to a standard distribution (such as the normal distribution). If you calculate a p-value , compare it to the significance level. If the p-value is less than the significance level, reject the null hypothesis.

Alternatively, you can compare your test statistic to a critical value from statistical tables to determine if you should reject the null hypothesis.

Step 5: Make a Decision

Based on your calculations:

• If the p-value is less than the significance level (e.g., p < 0.05), reject the null hypothesis.
• If the p-value is greater than the significance level, do not reject the null hypothesis.

Step 6: Interpret the Results

Finally, interpret the results in context. If you reject the null hypothesis, you have evidence to support the alternative hypothesis. If not, the data does not provide enough evidence to reject the null.

P-Value and Significance

The p-value is a key part of hypothesis testing. It tells us the likelihood of getting results as extreme as the observed data, assuming the null hypothesis is true. In simple terms:

• A low p-value (≤ 0.05) suggests strong evidence against the null hypothesis, so you reject it.
• A high p-value (> 0.05) means the data is consistent with the null hypothesis, and you don’t reject it.

Here’s a table to summarize:

Common Hypothesis Tests

There are different types of hypothesis tests depending on the data and what you are testing for.

Example of Hypothesis Testing

Let’s say a nutritionist claims that a new diet increases the average weight loss for people by 5 kg in a month.

• Null Hypothesis (H₀): The average weight loss is not 5 kg (no difference).
• Alternative Hypothesis (H₁): The average weight loss is greater than 5 kg.

Suppose we collect data from 30 people and find that the average weight loss is 5.5 kg. Now we follow these steps:

• Significance level : Set α = 0.05 (5%).
• Calculate the test statistic: Using the T-test formula.
• Find the p-value : Calculate the p-value for the test statistic.
• Make a decision : Compare the p-value to the significance level.

If the p-value is less than 0.05, we reject the null hypothesis and conclude that the new diet results in more than 5 kg of weight loss.

Statistical hypothesis testing is an essential method in statistics for making informed decisions based on data. By understanding the basics of null and alternative hypotheses, test statistics, p-values, and the steps in hypothesis testing, you can analyze experiments and surveys effectively.

Hypothesis testing is a powerful tool for everything from scientific research to everyday decisions, and mastering it can lead to better data analysis and decision-making.

Also Read: Step-by-step guide to hypothesis testing in statistics

What is the difference between the null hypothesis and the alternative hypothesis?

The null hypothesis (H₀) is the default assumption that there is no effect or no difference. It’s what we try to disprove. The alternative hypothesis (H₁) is what you want to prove. It suggests that there is a significant effect or difference.

What is the difference between a one-tailed test and a two-tailed test?

A one-tailed test looks for evidence of an effect in one direction (either greater or smaller). A two-tailed test checks for evidence of an effect in both directions (whether greater or smaller), making it a more conservative test.

Can we always reject the null hypothesis if the p-value is less than 0.05?

Yes, if the p-value is less than 0.05 , we typically reject the null hypothesis. However, this does not guarantee that the alternative hypothesis is true; it simply indicates that the data provide strong evidence against it.

Related Posts

Step by Step Guide on The Best Way to Finance Car

The Best Way on How to Get Fund For Business to Grow it Efficiently

Leave a comment cancel reply.

Your email address will not be published. Required fields are marked *

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

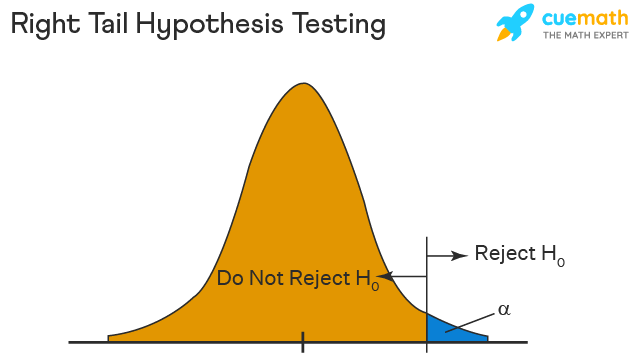
Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

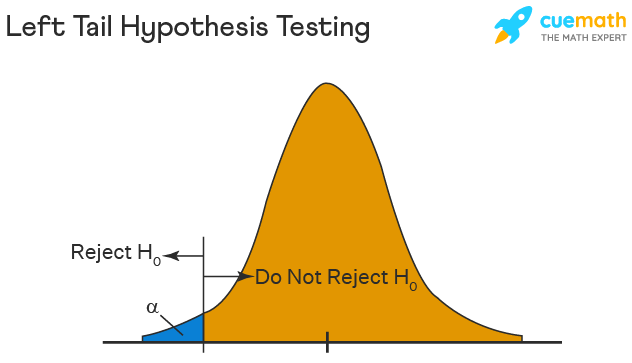
The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

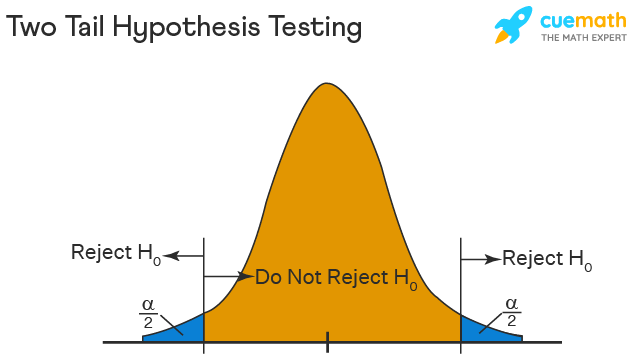
In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6a.2 - steps for hypothesis tests, the logic of hypothesis testing section  .

A hypothesis, in statistics, is a statement about a population parameter, where this statement typically is represented by some specific numerical value. In testing a hypothesis, we use a method where we gather data in an effort to gather evidence about the hypothesis.

How do we decide whether to reject the null hypothesis?

• If the sample data are consistent with the null hypothesis, then we do not reject it.
• If the sample data are inconsistent with the null hypothesis, but consistent with the alternative, then we reject the null hypothesis and conclude that the alternative hypothesis is true.

Six Steps for Hypothesis Tests Section  

In hypothesis testing, there are certain steps one must follow. Below these are summarized into six such steps to conducting a test of a hypothesis.

• Set up the hypotheses and check conditions : Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as \(H_0 \), which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is evidence to suggest otherwise. The second hypothesis is called the alternative, or research hypothesis, notated as \(H_a \). The alternative hypothesis is a statement of a range of alternative values in which the parameter may fall. One must also check that any conditions (assumptions) needed to run the test have been satisfied e.g. normality of data, independence, and number of success and failure outcomes.
• Decide on the significance level, \(\alpha \): This value is used as a probability cutoff for making decisions about the null hypothesis. This alpha value represents the probability we are willing to place on our test for making an incorrect decision in regards to rejecting the null hypothesis. The most common \(\alpha \) value is 0.05 or 5%. Other popular choices are 0.01 (1%) and 0.1 (10%).
• Calculate the test statistic: Gather sample data and calculate a test statistic where the sample statistic is compared to the parameter value. The test statistic is calculated under the assumption the null hypothesis is true and incorporates a measure of standard error and assumptions (conditions) related to the sampling distribution.
• Calculate probability value (p-value), or find the rejection region: A p-value is found by using the test statistic to calculate the probability of the sample data producing such a test statistic or one more extreme. The rejection region is found by using alpha to find a critical value; the rejection region is the area that is more extreme than the critical value. We discuss the p-value and rejection region in more detail in the next section.
• Make a decision about the null hypothesis: In this step, we decide to either reject the null hypothesis or decide to fail to reject the null hypothesis. Notice we do not make a decision where we will accept the null hypothesis.
• State an overall conclusion : Once we have found the p-value or rejection region, and made a statistical decision about the null hypothesis (i.e. we will reject the null or fail to reject the null), we then want to summarize our results into an overall conclusion for our test.

We will follow these six steps for the remainder of this Lesson. In the future Lessons, the steps will be followed but may not be explained explicitly.

Step 1 is a very important step to set up correctly. If your hypotheses are incorrect, your conclusion will be incorrect. In this next section, we practice with Step 1 for the one sample situations.

Hypothesis Testing - Chi Squared Test

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific tests considered here are called chi-square tests and are appropriate when the outcome is discrete (dichotomous, ordinal or categorical). For example, in some clinical trials the outcome is a classification such as hypertensive, pre-hypertensive or normotensive. We could use the same classification in an observational study such as the Framingham Heart Study to compare men and women in terms of their blood pressure status - again using the classification of hypertensive, pre-hypertensive or normotensive status.  

The technique to analyze a discrete outcome uses what is called a chi-square test. Specifically, the test statistic follows a chi-square probability distribution. We will consider chi-square tests here with one, two and more than two independent comparison groups.

Learning Objectives

After completing this module, the student will be able to:

• Perform chi-square tests by hand
• Appropriately interpret results of chi-square tests
• Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples

Tests with One Sample, Discrete Outcome

Here we consider hypothesis testing with a discrete outcome variable in a single population. Discrete variables are variables that take on more than two distinct responses or categories and the responses can be ordered or unordered (i.e., the outcome can be ordinal or categorical). The procedure we describe here can be used for dichotomous (exactly 2 response options), ordinal or categorical discrete outcomes and the objective is to compare the distribution of responses, or the proportions of participants in each response category, to a known distribution. The known distribution is derived from another study or report and it is again important in setting up the hypotheses that the comparator distribution specified in the null hypothesis is a fair comparison. The comparator is sometimes called an external or a historical control.   

In one sample tests for a discrete outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the proportions of participants in each response

Test Statistic for Testing H 0 : p 1 = p 10 , p 2 = p 20 , ..., p k = p k0

We find the critical value in a table of probabilities for the chi-square distribution with degrees of freedom (df) = k-1. In the test statistic, O = observed frequency and E=expected frequency in each of the response categories. The observed frequencies are those observed in the sample and the expected frequencies are computed as described below. χ 2 (chi-square) is another probability distribution and ranges from 0 to ∞. The test above statistic formula above is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories.  

When we conduct a χ 2 test, we compare the observed frequencies in each response category to the frequencies we would expect if the null hypothesis were true. These expected frequencies are determined by allocating the sample to the response categories according to the distribution specified in H 0 . This is done by multiplying the observed sample size (n) by the proportions specified in the null hypothesis (p 10 , p 20 , ..., p k0 ). To ensure that the sample size is appropriate for the use of the test statistic above, we need to ensure that the following: min(np 10 , n p 20 , ..., n p k0 ) > 5.  

The test of hypothesis with a discrete outcome measured in a single sample, where the goal is to assess whether the distribution of responses follows a known distribution, is called the χ 2 goodness-of-fit test. As the name indicates, the idea is to assess whether the pattern or distribution of responses in the sample "fits" a specified population (external or historical) distribution. In the next example we illustrate the test. As we work through the example, we provide additional details related to the use of this new test statistic.  

A University conducted a survey of its recent graduates to collect demographic and health information for future planning purposes as well as to assess students' satisfaction with their undergraduate experiences. The survey revealed that a substantial proportion of students were not engaging in regular exercise, many felt their nutrition was poor and a substantial number were smoking. In response to a question on regular exercise, 60% of all graduates reported getting no regular exercise, 25% reported exercising sporadically and 15% reported exercising regularly as undergraduates. The next year the University launched a health promotion campaign on campus in an attempt to increase health behaviors among undergraduates. The program included modules on exercise, nutrition and smoking cessation. To evaluate the impact of the program, the University again surveyed graduates and asked the same questions. The survey was completed by 470 graduates and the following data were collected on the exercise question:

Based on the data, is there evidence of a shift in the distribution of responses to the exercise question following the implementation of the health promotion campaign on campus? Run the test at a 5% level of significance.

In this example, we have one sample and a discrete (ordinal) outcome variable (with three response options). We specifically want to compare the distribution of responses in the sample to the distribution reported the previous year (i.e., 60%, 25%, 15% reporting no, sporadic and regular exercise, respectively). We now run the test using the five-step approach.  

• Step 1. Set up hypotheses and determine level of significance.

The null hypothesis again represents the "no change" or "no difference" situation. If the health promotion campaign has no impact then we expect the distribution of responses to the exercise question to be the same as that measured prior to the implementation of the program.

H 0 : p 1 =0.60, p 2 =0.25, p 3 =0.15,  or equivalently H 0 : Distribution of responses is 0.60, 0.25, 0.15  

H 1 :   H 0 is false.          α =0.05

Notice that the research hypothesis is written in words rather than in symbols. The research hypothesis as stated captures any difference in the distribution of responses from that specified in the null hypothesis. We do not specify a specific alternative distribution, instead we are testing whether the sample data "fit" the distribution in H 0 or not. With the χ 2 goodness-of-fit test there is no upper or lower tailed version of the test.

• Step 2. Select the appropriate test statistic.  

The test statistic is:

We must first assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=470 and the proportions specified in the null hypothesis are 0.60, 0.25 and 0.15. Thus, min( 470(0.65), 470(0.25), 470(0.15))=min(282, 117.5, 70.5)=70.5. The sample size is more than adequate so the formula can be used.

• Step 3. Set up decision rule.  

The decision rule for the χ 2 test depends on the level of significance and the degrees of freedom, defined as degrees of freedom (df) = k-1 (where k is the number of response categories). If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. Critical values can be found in a table of probabilities for the χ 2 distribution. Here we have df=k-1=3-1=2 and a 5% level of significance. The appropriate critical value is 5.99, and the decision rule is as follows: Reject H 0 if χ 2 > 5.99.

• Step 4. Compute the test statistic.  

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) and the expected frequencies into the formula for the test statistic identified in Step 2. The computations can be organized as follows.

Notice that the expected frequencies are taken to one decimal place and that the sum of the observed frequencies is equal to the sum of the expected frequencies. The test statistic is computed as follows:

• Step 5. Conclusion.  

We reject H 0 because 8.46 > 5.99. We have statistically significant evidence at α=0.05 to show that H 0 is false, or that the distribution of responses is not 0.60, 0.25, 0.15.  The p-value is p < 0.005.  

In the χ 2 goodness-of-fit test, we conclude that either the distribution specified in H 0 is false (when we reject H 0 ) or that we do not have sufficient evidence to show that the distribution specified in H 0 is false (when we fail to reject H 0 ). Here, we reject H 0 and concluded that the distribution of responses to the exercise question following the implementation of the health promotion campaign was not the same as the distribution prior. The test itself does not provide details of how the distribution has shifted. A comparison of the observed and expected frequencies will provide some insight into the shift (when the null hypothesis is rejected). Does it appear that the health promotion campaign was effective?  

Consider the following: 

If the null hypothesis were true (i.e., no change from the prior year) we would have expected more students to fall in the "No Regular Exercise" category and fewer in the "Regular Exercise" categories. In the sample, 255/470 = 54% reported no regular exercise and 90/470=19% reported regular exercise. Thus, there is a shift toward more regular exercise following the implementation of the health promotion campaign. There is evidence of a statistical difference, is this a meaningful difference? Is there room for improvement?

The National Center for Health Statistics (NCHS) provided data on the distribution of weight (in categories) among Americans in 2002. The distribution was based on specific values of body mass index (BMI) computed as weight in kilograms over height in meters squared. Underweight was defined as BMI< 18.5, Normal weight as BMI between 18.5 and 24.9, overweight as BMI between 25 and 29.9 and obese as BMI of 30 or greater. Americans in 2002 were distributed as follows: 2% Underweight, 39% Normal Weight, 36% Overweight, and 23% Obese. Suppose we want to assess whether the distribution of BMI is different in the Framingham Offspring sample. Using data from the n=3,326 participants who attended the seventh examination of the Offspring in the Framingham Heart Study we created the BMI categories as defined and observed the following:

• Step 1.  Set up hypotheses and determine level of significance.

H 0 : p 1 =0.02, p 2 =0.39, p 3 =0.36, p 4 =0.23     or equivalently

H 0 : Distribution of responses is 0.02, 0.39, 0.36, 0.23

H 1 :   H 0 is false.        α=0.05

The formula for the test statistic is:

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=3,326 and the proportions specified in the null hypothesis are 0.02, 0.39, 0.36 and 0.23. Thus, min( 3326(0.02), 3326(0.39), 3326(0.36), 3326(0.23))=min(66.5, 1297.1, 1197.4, 765.0)=66.5. The sample size is more than adequate, so the formula can be used.

Here we have df=k-1=4-1=3 and a 5% level of significance. The appropriate critical value is 7.81 and the decision rule is as follows: Reject H 0 if χ 2 > 7.81.

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) into the formula for the test statistic identified in Step 2. We organize the computations in the following table.

The test statistic is computed as follows:

We reject H 0 because 233.53 > 7.81. We have statistically significant evidence at α=0.05 to show that H 0 is false or that the distribution of BMI in Framingham is different from the national data reported in 2002, p < 0.005.  

Again, the χ 2   goodness-of-fit test allows us to assess whether the distribution of responses "fits" a specified distribution. Here we show that the distribution of BMI in the Framingham Offspring Study is different from the national distribution. To understand the nature of the difference we can compare observed and expected frequencies or observed and expected proportions (or percentages). The frequencies are large because of the large sample size, the observed percentages of patients in the Framingham sample are as follows: 0.6% underweight, 28% normal weight, 41% overweight and 30% obese. In the Framingham Offspring sample there are higher percentages of overweight and obese persons (41% and 30% in Framingham as compared to 36% and 23% in the national data), and lower proportions of underweight and normal weight persons (0.6% and 28% in Framingham as compared to 2% and 39% in the national data). Are these meaningful differences?

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable in a single population. We presented a test using a test statistic Z to test whether an observed (sample) proportion differed significantly from a historical or external comparator. The chi-square goodness-of-fit test can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square goodness-of-fit test.

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

We presented the following approach to the test using a Z statistic. 

• Step 1. Set up hypotheses and determine level of significance

H 0 : p = 0.75

H 1 : p ≠ 0.75                               α=0.05

We must first check that the sample size is adequate. Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 125(0.75), 125(1-0.75))=min(94, 31)=31. The sample size is more than adequate so the following formula can be used

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. The sample proportion is:

We reject H 0 because -6.15 < -1.960. We have statistically significant evidence at a =0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data. (p < 0.0001).  

We now conduct the same test using the chi-square goodness-of-fit test. First, we summarize our sample data as follows:

H 0 : p 1 =0.75, p 2 =0.25     or equivalently H 0 : Distribution of responses is 0.75, 0.25 

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ...,np k >) > 5. The sample size here is n=125 and the proportions specified in the null hypothesis are 0.75, 0.25. Thus, min( 125(0.75), 125(0.25))=min(93.75, 31.25)=31.25. The sample size is more than adequate so the formula can be used.

Here we have df=k-1=2-1=1 and a 5% level of significance. The appropriate critical value is 3.84, and the decision rule is as follows: Reject H 0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

(Note that (-6.15) 2 = 37.8, where -6.15 was the value of the Z statistic in the test for proportions shown above.)

We reject H 0 because 37.8 > 3.84. We have statistically significant evidence at α=0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data.  (p < 0.0001). This is the same conclusion we reached when we conducted the test using the Z test above. With a dichotomous outcome, Z 2 = χ 2 !   In statistics, there are often several approaches that can be used to test hypotheses. 

Tests for Two or More Independent Samples, Discrete Outcome

Here we extend that application of the chi-square test to the case with two or more independent comparison groups. Specifically, the outcome of interest is discrete with two or more responses and the responses can be ordered or unordered (i.e., the outcome can be dichotomous, ordinal or categorical). We now consider the situation where there are two or more independent comparison groups and the goal of the analysis is to compare the distribution of responses to the discrete outcome variable among several independent comparison groups.  

The test is called the χ 2 test of independence and the null hypothesis is that there is no difference in the distribution of responses to the outcome across comparison groups. This is often stated as follows: The outcome variable and the grouping variable (e.g., the comparison treatments or comparison groups) are independent (hence the name of the test). Independence here implies homogeneity in the distribution of the outcome among comparison groups.    

The null hypothesis in the χ 2 test of independence is often stated in words as: H 0 : The distribution of the outcome is independent of the groups. The alternative or research hypothesis is that there is a difference in the distribution of responses to the outcome variable among the comparison groups (i.e., that the distribution of responses "depends" on the group). In order to test the hypothesis, we measure the discrete outcome variable in each participant in each comparison group. The data of interest are the observed frequencies (or number of participants in each response category in each group). The formula for the test statistic for the χ 2 test of independence is given below.

Test Statistic for Testing H 0 : Distribution of outcome is independent of groups

and we find the critical value in a table of probabilities for the chi-square distribution with df=(r-1)*(c-1).

Here O = observed frequency, E=expected frequency in each of the response categories in each group, r = the number of rows in the two-way table and c = the number of columns in the two-way table.   r and c correspond to the number of comparison groups and the number of response options in the outcome (see below for more details). The observed frequencies are the sample data and the expected frequencies are computed as described below. The test statistic is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories in each group.  

The data for the χ 2 test of independence are organized in a two-way table. The outcome and grouping variable are shown in the rows and columns of the table. The sample table below illustrates the data layout. The table entries (blank below) are the numbers of participants in each group responding to each response category of the outcome variable.

Table - Possible outcomes are are listed in the columns; The groups being compared are listed in rows.

In the table above, the grouping variable is shown in the rows of the table; r denotes the number of independent groups. The outcome variable is shown in the columns of the table; c denotes the number of response options in the outcome variable. Each combination of a row (group) and column (response) is called a cell of the table. The table has r*c cells and is sometimes called an r x c ("r by c") table. For example, if there are 4 groups and 5 categories in the outcome variable, the data are organized in a 4 X 5 table. The row and column totals are shown along the right-hand margin and the bottom of the table, respectively. The total sample size, N, can be computed by summing the row totals or the column totals. Similar to ANOVA, N does not refer to a population size here but rather to the total sample size in the analysis. The sample data can be organized into a table like the above. The numbers of participants within each group who select each response option are shown in the cells of the table and these are the observed frequencies used in the test statistic.

The test statistic for the χ 2 test of independence involves comparing observed (sample data) and expected frequencies in each cell of the table. The expected frequencies are computed assuming that the null hypothesis is true. The null hypothesis states that the two variables (the grouping variable and the outcome) are independent. The definition of independence is as follows:

 Two events, A and B, are independent if P(A|B) = P(A), or equivalently, if P(A and B) = P(A) P(B).

The second statement indicates that if two events, A and B, are independent then the probability of their intersection can be computed by multiplying the probability of each individual event. To conduct the χ 2 test of independence, we need to compute expected frequencies in each cell of the table. Expected frequencies are computed by assuming that the grouping variable and outcome are independent (i.e., under the null hypothesis). Thus, if the null hypothesis is true, using the definition of independence:

P(Group 1 and Response Option 1) = P(Group 1) P(Response Option 1).

 The above states that the probability that an individual is in Group 1 and their outcome is Response Option 1 is computed by multiplying the probability that person is in Group 1 by the probability that a person is in Response Option 1. To conduct the χ 2 test of independence, we need expected frequencies and not expected probabilities . To convert the above probability to a frequency, we multiply by N. Consider the following small example.

The data shown above are measured in a sample of size N=150. The frequencies in the cells of the table are the observed frequencies. If Group and Response are independent, then we can compute the probability that a person in the sample is in Group 1 and Response category 1 using:

P(Group 1 and Response 1) = P(Group 1) P(Response 1),

P(Group 1 and Response 1) = (25/150) (62/150) = 0.069.

Thus if Group and Response are independent we would expect 6.9% of the sample to be in the top left cell of the table (Group 1 and Response 1). The expected frequency is 150(0.069) = 10.4.   We could do the same for Group 2 and Response 1:

P(Group 2 and Response 1) = P(Group 2) P(Response 1),

P(Group 2 and Response 1) = (50/150) (62/150) = 0.138.

The expected frequency in Group 2 and Response 1 is 150(0.138) = 20.7.

Thus, the formula for determining the expected cell frequencies in the χ 2 test of independence is as follows:

Expected Cell Frequency = (Row Total * Column Total)/N.

The above computes the expected frequency in one step rather than computing the expected probability first and then converting to a frequency.  

In a prior example we evaluated data from a survey of university graduates which assessed, among other things, how frequently they exercised. The survey was completed by 470 graduates. In the prior example we used the χ 2 goodness-of-fit test to assess whether there was a shift in the distribution of responses to the exercise question following the implementation of a health promotion campaign on campus. We specifically considered one sample (all students) and compared the observed distribution to the distribution of responses the prior year (a historical control). Suppose we now wish to assess whether there is a relationship between exercise on campus and students' living arrangements. As part of the same survey, graduates were asked where they lived their senior year. The response options were dormitory, on-campus apartment, off-campus apartment, and at home (i.e., commuted to and from the university). The data are shown below.

Based on the data, is there a relationship between exercise and student's living arrangement? Do you think where a person lives affect their exercise status? Here we have four independent comparison groups (living arrangement) and a discrete (ordinal) outcome variable with three response options. We specifically want to test whether living arrangement and exercise are independent. We will run the test using the five-step approach.  

H 0 : Living arrangement and exercise are independent

H 1 : H 0 is false.                α=0.05

The null and research hypotheses are written in words rather than in symbols. The research hypothesis is that the grouping variable (living arrangement) and the outcome variable (exercise) are dependent or related.   

• Step 2.  Select the appropriate test statistic.  

The condition for appropriate use of the above test statistic is that each expected frequency is at least 5. In Step 4 we will compute the expected frequencies and we will ensure that the condition is met.

The decision rule depends on the level of significance and the degrees of freedom, defined as df = (r-1)(c-1), where r and c are the numbers of rows and columns in the two-way data table.   The row variable is the living arrangement and there are 4 arrangements considered, thus r=4. The column variable is exercise and 3 responses are considered, thus c=3. For this test, df=(4-1)(3-1)=3(2)=6. Again, with χ 2 tests there are no upper, lower or two-tailed tests. If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. The rejection region for the χ 2 test of independence is always in the upper (right-hand) tail of the distribution. For df=6 and a 5% level of significance, the appropriate critical value is 12.59 and the decision rule is as follows: Reject H 0 if c 2 > 12.59.

We now compute the expected frequencies using the formula,

Expected Frequency = (Row Total * Column Total)/N.

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency.   The expected frequencies are shown in parentheses.

Notice that the expected frequencies are taken to one decimal place and that the sums of the observed frequencies are equal to the sums of the expected frequencies in each row and column of the table.  

Recall in Step 2 a condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 9.6) and therefore it is appropriate to use the test statistic.

We reject H 0 because 60.5 > 12.59. We have statistically significant evidence at a =0.05 to show that H 0 is false or that living arrangement and exercise are not independent (i.e., they are dependent or related), p < 0.005.  

Again, the χ 2 test of independence is used to test whether the distribution of the outcome variable is similar across the comparison groups. Here we rejected H 0 and concluded that the distribution of exercise is not independent of living arrangement, or that there is a relationship between living arrangement and exercise. The test provides an overall assessment of statistical significance. When the null hypothesis is rejected, it is important to review the sample data to understand the nature of the relationship. Consider again the sample data. 

Because there are different numbers of students in each living situation, it makes the comparisons of exercise patterns difficult on the basis of the frequencies alone. The following table displays the percentages of students in each exercise category by living arrangement. The percentages sum to 100% in each row of the table. For comparison purposes, percentages are also shown for the total sample along the bottom row of the table.

From the above, it is clear that higher percentages of students living in dormitories and in on-campus apartments reported regular exercise (31% and 23%) as compared to students living in off-campus apartments and at home (10% each).  

Test Yourself

 Pancreaticoduodenectomy (PD) is a procedure that is associated with considerable morbidity. A study was recently conducted on 553 patients who had a successful PD between January 2000 and December 2010 to determine whether their Surgical Apgar Score (SAS) is related to 30-day perioperative morbidity and mortality. The table below gives the number of patients experiencing no, minor, or major morbidity by SAS category.  

Question: What would be an appropriate statistical test to examine whether there is an association between Surgical Apgar Score and patient outcome? Using 14.13 as the value of the test statistic for these data, carry out the appropriate test at a 5% level of significance. Show all parts of your test.

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable and two independent comparison groups. We presented a test using a test statistic Z to test for equality of independent proportions. The chi-square test of independence can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square test of independence.

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We tested whether there was a significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using a Z statistic, as follows. 

H 0 : p 1 = p 2    

H 1 : p 1 ≠ p 2                             α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group or that:

In this example, we have

Therefore, the sample size is adequate, so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5.  Conclusion.  

We now conduct the same test using the chi-square test of independence.  

H 0 : Treatment and outcome (meaningful reduction in pain) are independent

H 1 :   H 0 is false.         α=0.05

The formula for the test statistic is:  

For this test, df=(2-1)(2-1)=1. At a 5% level of significance, the appropriate critical value is 3.84 and the decision rule is as follows: Reject H0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

We now compute the expected frequencies using:

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency. The expected frequencies are shown in parentheses.

A condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 22.0) and therefore it is appropriate to use the test statistic.

(Note that (2.53) 2 = 6.4, where 2.53 was the value of the Z statistic in the test for proportions shown above.)

Chi-Squared Tests in R

The video below by Mike Marin demonstrates how to perform chi-squared tests in the R programming language.

Answer to Problem on Pancreaticoduodenectomy and Surgical Apgar Scores

We have 3 independent comparison groups (Surgical Apgar Score) and a categorical outcome variable (morbidity/mortality). We can run a Chi-Squared test of independence.

H 0 : Apgar scores and patient outcome are independent of one another.

H A : Apgar scores and patient outcome are not independent.

Chi-squared = 14.3

Since 14.3 is greater than 9.49, we reject H 0.

There is an association between Apgar scores and patient outcome. The lowest Apgar score group (0 to 4) experienced the highest percentage of major morbidity or mortality (16 out of 57=28%) compared to the other Apgar score groups.

What is Hypothesis Testing in Statistics? Types and Examples

Varun Saharawat is a seasoned professional in the fields of SEO and content writing. With a profound knowledge of the intricate aspects of these disciplines, Varun has established himself as a valuable asset in the world of digital marketing and online content creation.

Hypothesis testing in statistics involves testing an assumption about a population parameter using sample data. Learners can download Hypothesis Testing PDF to get instant access to all information!

What exactly is hypothesis testing, and how does it work in statistics? Can I find practical examples and understand the different types from this blog?

Hypothesis Testing : Ever wonder how researchers determine if a new medicine actually works or if a new marketing campaign effectively drives sales? They use hypothesis testing! It is at the core of how scientific studies, business experiments and surveys determine if their results are statistically significant or just due to chance.

Hypothesis testing allows us to make evidence-based decisions by quantifying uncertainty and providing a structured process to make data-driven conclusions rather than guessing. In this post, we will discuss hypothesis testing types, examples, and processes!

Table of Contents

Hypothesis Testing

Hypothesis testing is a statistical method used to evaluate the validity of a hypothesis using sample data. It involves assessing whether observed data provide enough evidence to reject a specific hypothesis about a population parameter. 

Hypothesis Testing in Data Science

Hypothesis testing in data science is a statistical method used to evaluate two mutually exclusive population statements based on sample data. The primary goal is to determine which statement is more supported by the observed data.

Hypothesis testing assists in supporting the certainty of findings in research and data science projects. This statistical inference aids in making decisions about population parameters using sample data. For those who are looking to deepen their knowledge in data science and expand their skillset, we highly recommend checking out Master Generative AI: Data Science Course by Physics Wallah .

Also Read: What is Encapsulation Explain in Details

What is the Hypothesis Testing Procedure in Data Science?

The hypothesis testing procedure in data science involves a structured approach to evaluating hypotheses using statistical methods. Here’s a step-by-step breakdown of the typical procedure:

1) State the Hypotheses:

• Null Hypothesis (H0): This is the default assumption or a statement of no effect or difference. It represents what you aim to test against.
• Alternative Hypothesis (Ha): This is the opposite of the null hypothesis and represents what you want to prove.

2) Choose a Significance Level (α):

• Decide on a threshold (commonly 0.05) beyond which you will reject the null hypothesis. This is your significance level.

3) Select the Appropriate Test:

• Depending on your data type (e.g., continuous, categorical) and the nature of your research question, choose the appropriate statistical test (e.g., t-test, chi-square test, ANOVA, etc.).

4) Collect Data:

• Gather data from your sample or population, ensuring that it’s representative and sufficiently large (or as per your experimental design).

5)Compute the Test Statistic:

• Using your data and the chosen statistical test, compute the test statistic that summarizes the evidence against the null hypothesis.

6) Determine the Critical Value or P-value:

• Based on your significance level and the test statistic’s distribution, determine the critical value from a statistical table or compute the p-value.

7) Make a Decision:

• If the p-value is less than α: Reject the null hypothesis.
• If the p-value is greater than or equal to α: Fail to reject the null hypothesis.

8) Draw Conclusions:

• Based on your decision, draw conclusions about your research question or hypothesis. Remember, failing to reject the null hypothesis doesn’t prove it true; it merely suggests that you don’t have sufficient evidence to reject it.

9) Report Findings:

• Document your findings, including the test statistic, p-value, conclusion, and any other relevant details. Ensure clarity so that others can understand and potentially replicate your analysis.

Also Read: Binary Search Algorithm

How Hypothesis Testing Works?

Hypothesis testing is a fundamental concept in statistics that aids analysts in making informed decisions based on sample data about a larger population. The process involves setting up two contrasting hypotheses, the null hypothesis and the alternative hypothesis, and then using statistical methods to determine which hypothesis provides a more plausible explanation for the observed data.

The Core Principles:

• The Null Hypothesis (H0): This serves as the default assumption or status quo. Typically, it posits that there is no effect or no difference, often represented by an equality statement regarding population parameters. For instance, it might state that a new drug’s effect is no different from a placebo.
• The Alternative Hypothesis (H1 or Ha): This is the counter assumption or what researchers aim to prove. It’s the opposite of the null hypothesis, indicating that there is an effect, a change, or a difference in the population parameters. Using the drug example, the alternative hypothesis would suggest that the new drug has a different effect than the placebo.

Testing the Hypotheses:

Once these hypotheses are established, analysts gather data from a sample and conduct statistical tests. The objective is to determine whether the observed results are statistically significant enough to reject the null hypothesis in favor of the alternative.

Examples to Clarify the Concept:

• Null Hypothesis (H0): The sanitizer’s average efficacy is 95%.
• By conducting tests, if evidence suggests that the sanitizer’s efficacy is significantly less than 95%, we reject the null hypothesis.
• Null Hypothesis (H0): The coin is fair, meaning the probability of heads and tails is equal.
• Through experimental trials, if results consistently show a skewed outcome, indicating a significantly different probability for heads and tails, the null hypothesis might be rejected.

What are the 3 types of Hypothesis Test?

Hypothesis testing is a cornerstone in statistical analysis, providing a framework to evaluate the validity of assumptions or claims made about a population based on sample data. Within this framework, several specific tests are utilized based on the nature of the data and the question at hand. Here’s a closer look at the three fundamental types of hypothesis tests:

The z-test is a statistical method primarily employed when comparing means from two datasets, particularly when the population standard deviation is known. Its main objective is to ascertain if the means are statistically equivalent. 

A crucial prerequisite for the z-test is that the sample size should be relatively large, typically 30 data points or more. This test aids researchers and analysts in determining the significance of a relationship or discovery, especially in scenarios where the data’s characteristics align with the assumptions of the z-test.

The t-test is a versatile statistical tool used extensively in research and various fields to compare means between two groups. It’s particularly valuable when the population standard deviation is unknown or when dealing with smaller sample sizes. 

By evaluating the means of two groups, the t-test helps ascertain if a particular treatment, intervention, or variable significantly impacts the population under study. Its flexibility and robustness make it a go-to method in scenarios ranging from medical research to business analytics.

3. Chi-Square Test:

The Chi-Square test stands distinct from the previous tests, primarily focusing on categorical data rather than means. This statistical test is instrumental when analyzing categorical variables to determine if observed data aligns with expected outcomes as posited by the null hypothesis. 

By assessing the differences between observed and expected frequencies within categorical data, the Chi-Square test offers insights into whether discrepancies are statistically significant. Whether used in social sciences to evaluate survey responses or in quality control to assess product defects, the Chi-Square test remains pivotal for hypothesis testing in diverse scenarios.

Also Read: Python vs Java: Which is Best for Machine learning algorithm

Hypothesis Testing in Statistics

Hypothesis testing is a fundamental concept in statistics used to make decisions or inferences about a population based on a sample of data. The process involves setting up two competing hypotheses, the null hypothesis H 0​ and the alternative hypothesis H 1​. 

Through various statistical tests, such as the t-test, z-test, or Chi-square test, analysts evaluate sample data to determine whether there’s enough evidence to reject the null hypothesis in favor of the alternative. The aim is to draw conclusions about population parameters or to test theories, claims, or hypotheses.

Hypothesis Testing in Research

In research, hypothesis testing serves as a structured approach to validate or refute theories or claims. Researchers formulate a clear hypothesis based on existing literature or preliminary observations. They then collect data through experiments, surveys, or observational studies. 

Using statistical methods, researchers analyze this data to determine if there’s sufficient evidence to reject the null hypothesis. By doing so, they can draw meaningful conclusions, make predictions, or recommend actions based on empirical evidence rather than mere speculation.

Hypothesis Testing in R

R, a powerful programming language and environment for statistical computing and graphics, offers a wide array of functions and packages specifically designed for hypothesis testing. Here’s how hypothesis testing is conducted in R:

• Data Collection : Before conducting any test, you need to gather your data and ensure it’s appropriately structured in R.
• Choose the Right Test : Depending on your research question and data type, select the appropriate hypothesis test. For instance, use the t.test() function for a t-test or chisq.test() for a Chi-square test.
• Set Hypotheses : Define your null and alternative hypotheses. Using R’s syntax, you can specify these hypotheses and run the corresponding test.
• Execute the Test : Utilize built-in functions in R to perform the hypothesis test on your data. For instance, if you want to compare two means, you can use the t.test() function, providing the necessary arguments like the data vectors and type of t-test (one-sample, two-sample, paired, etc.).
• Interpret Results : Once the test is executed, R will provide output, including test statistics, p-values, and confidence intervals. Based on these results and a predetermined significance level (often 0.05), you can decide whether to reject the null hypothesis.
• Visualization : R’s graphical capabilities allow users to visualize data distributions, confidence intervals, or test statistics, aiding in the interpretation and presentation of results.

Hypothesis testing is an integral part of statistics and research, offering a systematic approach to validate hypotheses. Leveraging R’s capabilities, researchers and analysts can efficiently conduct and interpret various hypothesis tests, ensuring robust and reliable conclusions from their data.

Do Data Scientists do Hypothesis Testing?

Yes, data scientists frequently engage in hypothesis testing as part of their analytical toolkit. Hypothesis testing is a foundational statistical technique used to make data-driven decisions, validate assumptions, and draw conclusions from data. Here’s how data scientists utilize hypothesis testing:

• Validating Assumptions : Before diving into complex analyses or building predictive models, data scientists often need to verify certain assumptions about the data. Hypothesis testing provides a structured approach to test these assumptions, ensuring that subsequent analyses or models are valid.
• Feature Selection : In machine learning and predictive modeling, data scientists use hypothesis tests to determine which features (or variables) are most relevant or significant in predicting a particular outcome. By testing hypotheses related to feature importance or correlation, they can streamline the modeling process and enhance prediction accuracy.
• A/B Testing : A/B testing is a common technique in marketing, product development, and user experience design. Data scientists employ hypothesis testing to compare two versions (A and B) of a product, feature, or marketing strategy to determine which performs better in terms of a specified metric (e.g., conversion rate, user engagement).
• Research and Exploration : In exploratory data analysis (EDA) or when investigating specific research questions, data scientists formulate hypotheses to test certain relationships or patterns within the data. By conducting hypothesis tests, they can validate these relationships, uncover insights, and drive data-driven decision-making.
• Model Evaluation : After building machine learning or statistical models, data scientists use hypothesis testing to evaluate the model’s performance, assess its predictive power, or compare different models. For instance, hypothesis tests like the t-test or F-test can help determine if a new model significantly outperforms an existing one based on certain metrics.
• Business Decision-making : Beyond technical analyses, data scientists employ hypothesis testing to support business decisions. Whether it’s evaluating the effectiveness of a marketing campaign, assessing customer preferences, or optimizing operational processes, hypothesis testing provides a rigorous framework to validate assumptions and guide strategic initiatives.

Hypothesis Testing Examples and Solutions

Let’s delve into some common examples of hypothesis testing and provide solutions or interpretations for each scenario.

Example: Testing the Mean

Scenario : A coffee shop owner believes that the average waiting time for customers during peak hours is 5 minutes. To test this, the owner takes a random sample of 30 customer waiting times and wants to determine if the average waiting time is indeed 5 minutes.

Hypotheses :

• H 0​ (Null Hypothesis): 5 μ =5 minutes (The average waiting time is 5 minutes)
• H 1​ (Alternative Hypothesis): 5 μ =5 minutes (The average waiting time is not 5 minutes)

Solution : Using a t-test (assuming population variance is unknown), calculate the t-statistic based on the sample mean, sample standard deviation, and sample size. Then, determine the p-value and compare it with a significance level (e.g., 0.05) to decide whether to reject the null hypothesis.

Example: A/B Testing in Marketing

Scenario : An e-commerce company wants to determine if changing the color of a “Buy Now” button from blue to green increases the conversion rate.

• H 0​: Changing the button color does not affect the conversion rate.
• H 1​: Changing the button color affects the conversion rate.

Solution : Split website visitors into two groups: one sees the blue button (control group), and the other sees the green button (test group). Track the conversion rates for both groups over a specified period. Then, use a chi-square test or z-test (for large sample sizes) to determine if there’s a statistically significant difference in conversion rates between the two groups.

Hypothesis Testing Formula

The formula for hypothesis testing typically depends on the type of test (e.g., z-test, t-test, chi-square test) and the nature of the data (e.g., mean, proportion, variance). Below are the basic formulas for some common hypothesis tests:

Z-Test for Population Mean :

Z=(σ/n​)(xˉ−μ0​)​

• ˉ x ˉ = Sample mean
• 0 μ 0​ = Population mean under the null hypothesis
• σ = Population standard deviation
• n = Sample size

T-Test for Population Mean :

t= (s/ n ​ ) ( x ˉ −μ 0 ​ ) ​ 

s = Sample standard deviation 

Chi-Square Test for Goodness of Fit :

χ2=∑Ei​(Oi​−Ei​)2​

• Oi ​ = Observed frequency
• Ei ​ = Expected frequency

Also Read: Full Form of OOPS

Hypothesis Testing Calculator

While you can perform hypothesis testing manually using the above formulas and statistical tables, many online tools and software packages simplify this process. Here’s how you might use a calculator or software:

• Z-Test and T-Test Calculators : These tools typically require you to input sample statistics (like sample mean, population mean, standard deviation, and sample size). Once you input these values, the calculator will provide you with the test statistic (Z or t) and a p-value.
• Chi-Square Calculator : For chi-square tests, you’d input observed and expected frequencies for different categories or groups. The calculator then computes the chi-square statistic and provides a p-value.
• Software Packages (e.g., R, Python with libraries like scipy, or statistical software like SPSS) : These platforms offer more comprehensive tools for hypothesis testing. You can run various tests, get detailed outputs, and even perform advanced analyses, including regression models, ANOVA, and more.

When using any calculator or software, always ensure you understand the underlying assumptions of the test, interpret the results correctly, and consider the broader context of your research or analysis.

Hypothesis Testing FAQs

What are the key components of a hypothesis test.

The key components include: Null Hypothesis (H0): A statement of no effect or no difference. Alternative Hypothesis (H1 or Ha): A statement that contradicts the null hypothesis. Test Statistic: A value computed from the sample data to test the null hypothesis. Significance Level (α): The threshold for rejecting the null hypothesis. P-value: The probability of observing the given data, assuming the null hypothesis is true.

What is the significance level in hypothesis testing?

The significance level (often denoted as α) is the probability threshold used to determine whether to reject the null hypothesis. Commonly used values for α include 0.05, 0.01, and 0.10, representing a 5%, 1%, or 10% chance of rejecting the null hypothesis when it's actually true.

How do I choose between a one-tailed and two-tailed test?

The choice between one-tailed and two-tailed tests depends on your research question and hypothesis. Use a one-tailed test when you're specifically interested in one direction of an effect (e.g., greater than or less than). Use a two-tailed test when you want to determine if there's a significant difference in either direction.

What is a p-value, and how is it interpreted?

The p-value is a probability value that helps determine the strength of evidence against the null hypothesis. A low p-value (typically ≤ 0.05) suggests that the observed data is inconsistent with the null hypothesis, leading to its rejection. Conversely, a high p-value suggests that the data is consistent with the null hypothesis, leading to no rejection.

Can hypothesis testing prove a hypothesis true?

No, hypothesis testing cannot prove a hypothesis true. Instead, it helps assess the likelihood of observing a given set of data under the assumption that the null hypothesis is true. Based on this assessment, you either reject or fail to reject the null hypothesis.

• CS Fundamentals – Computer Fundamental Tutorial

CS Fundamentals consist of basics of computer systems such as hardware, software, networking and more. It consists of knowledge of…

• Computer Basic Class Offers Basic Understanding of Fundamentals of Computers

Computer basic class offers basic understanding of fundamentals of computers and related technologies. If you are a tech enthusiast and…

• Step-by-Step Guide to Buy Courses on PW Skills

PW Skills offers an accessible and comprehensive learning experience for learners of all levels. It covers a Data Science course and…

Related Articles

• Why Choose PW Skills to Learn Coding Course?
• Data Science Vs Machine Learning [Updated]
• Big Data vs Data science
• Top 10 Career Options after BCA
• Top 12 Highest Salary Jobs in India
• Network Engineer Salary in India
• Future of Prompt Engineering in 2023 with Career Guide

• Python for Data Science
• Data Analysis
• Machine Learning
• Deep Learning
• Deep Learning Interview Questions
• ML Projects
• ML Interview Questions

Understanding Hypothesis Testing

Hypothesis testing is a fundamental statistical method employed in various fields, including data science , machine learning , and statistics , to make informed decisions based on empirical evidence. It involves formulating assumptions about population parameters using sample statistics and rigorously evaluating these assumptions against collected data. At its core, hypothesis testing is a systematic approach that allows researchers to assess the validity of a statistical claim about an unknown population parameter. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

Table of Content

What is Hypothesis Testing?

Why do we use hypothesis testing, one-tailed and two-tailed test, what are type 1 and type 2 errors in hypothesis testing, how does hypothesis testing work, real life examples of hypothesis testing, limitations of hypothesis testing.

A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

To test the validity of the claim or assumption about the population parameter:

• A sample is drawn from the population and analyzed.
• The results of the analysis are used to decide whether the claim is true or not.

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

This structured approach to hypothesis testing in data science , hypothesis testing in machine learning , and hypothesis testing in statistics is crucial for making informed decisions based on data.

• By employing hypothesis testing in data analytics and other fields, practitioners can rigorously evaluate their assumptions and derive meaningful insights from their analyses.
• Understanding hypothesis generation and testing is also essential for effectively implementing statistical hypothesis testing in various applications.

Defining Hypotheses

• Null hypothesis (H 0 ): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example : A company’s mean production is 50 units/per da H 0 : [Tex]\mu [/Tex] = 50.
• Alternative hypothesis (H 1 ): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis.  Example: A company’s production is not equal to 50 units/per day i.e. H 1 : [Tex]\mu [/Tex] [Tex]\ne [/Tex] 50.

Key Terms of Hypothesis Testing

• Level of significance : It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with  [Tex]\alpha[/Tex] and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.

Understanding hypothesis testing in statistics is essential for data scientists and machine learning practitioners, as it provides a structured framework for statistical hypothesis generation and testing. This methodology can also be applied in hypothesis testing in Python , enabling data analysts to perform robust statistical analyses efficiently. By employing techniques such as multiple hypothesis testing in machine learning , researchers can ensure more reliable results and avoid potential pitfalls associated with drawing conclusions from statistical tests. 

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

• Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H 0 ​: [Tex]\mu \geq 50 [/Tex] and H 1 : [Tex]\mu < 50 [/Tex]
• Right-Tailed (Right-Sided) Test : The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H 0 : [Tex]\mu \leq50 [/Tex] and H 1 : [Tex]\mu > 50 [/Tex]

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

Example: H 0 : [Tex]\mu = [/Tex] 50 and H 1 : [Tex]\mu \neq 50 [/Tex]

To delve deeper into differences into both types of test: Refer to link

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

• Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha( [Tex]\alpha [/Tex] ).
• Type II errors : When we accept the null hypothesis, but it is false. Type II errors are denoted by beta( [Tex]\beta [/Tex] ).

Step 1: Define Null and Alternative Hypothesis

State the null hypothesis ( [Tex]H_0 [/Tex] ), representing no effect, and the alternative hypothesis ( [Tex]H_1 [/Tex] ​), suggesting an effect or difference.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Select a significance level ( [Tex]\alpha [/Tex] ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

• If the p-value is less than or equal to the significance level i.e. ( [Tex]p\leq\alpha [/Tex] ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
• If the p-value is greater than the significance level i.e. ( [Tex]p\geq \alpha[/Tex] ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

[Tex]z = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}[/Tex]

• [Tex]\bar{x} [/Tex] is the sample mean,
• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

[Tex]t=\frac{x̄-μ}{s/\sqrt{n}} [/Tex]

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

[Tex]\chi^2 = \sum \frac{(O_{ij} – E_{ij})^2}{E_{ij}}[/Tex]

• [Tex]O_{ij}[/Tex] is the observed frequency in cell [Tex]{ij} [/Tex]
• i,j are the rows and columns index respectively.
• [Tex]E_{ij}[/Tex] is the expected frequency in cell [Tex]{ij}[/Tex] , calculated as : [Tex]\frac{{\text{{Row total}} \times \text{{Column total}}}}{{\text{{Total observations}}}}[/Tex]

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Case A

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

T-statistic (from scipy): -9.0 P-value (from scipy): 8.538051223166285e-06 T-statistic (calculated manually): -9.0 Decision: Reject the null hypothesis at alpha=0.05. Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

The test statistic is calculated by using the z formula Z = [Tex](203.8 – 200) / (5 \div \sqrt{25}) [/Tex] ​ and we get accordingly , Z =2.039999999999992.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Python Implementation of Case B

Reject the null hypothesis. There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.

Although hypothesis testing is a useful technique in data science , it does not offer a comprehensive grasp of the topic being studied.

• Lack of Comprehensive Insight : Hypothesis testing in data science often focuses on specific hypotheses, which may not fully capture the complexity of the phenomena being studied.
• Dependence on Data Quality : The accuracy of hypothesis testing results relies heavily on the quality of available data. Inaccurate data can lead to incorrect conclusions, particularly in hypothesis testing in machine learning .
• Overlooking Patterns : Sole reliance on hypothesis testing can result in the omission of significant patterns or relationships in the data that are not captured by the tested hypotheses.
• Contextual Limitations : Hypothesis testing in statistics may not reflect the broader context, leading to oversimplification of results.
• Complementary Methods Needed : To gain a more holistic understanding, it’s essential to complement hypothesis testing with other analytical approaches, especially in data analytics and data mining .
• Misinterpretation Risks : Poorly formulated hypotheses or inappropriate statistical methods can lead to misinterpretation, emphasizing the need for careful consideration in hypothesis testing in Python and related analyses.
• Multiple Hypothesis Testing Challenges : Multiple hypothesis testing in machine learning poses additional challenges, as it can increase the likelihood of Type I errors, requiring adjustments to maintain validity.

Hypothesis testing is a cornerstone of statistical analysis , allowing data scientists to navigate uncertainties and draw credible inferences from sample data. By defining null and alternative hypotheses, selecting significance levels, and employing statistical tests, researchers can validate their assumptions effectively.

This article emphasizes the distinction between Type I and Type II errors, highlighting their relevance in hypothesis testing in data science and machine learning . A practical example involving a paired T-test to assess a new drug’s effect on blood pressure underscores the importance of statistical rigor in data-driven decision-making .

Ultimately, understanding hypothesis testing in statistics , alongside its applications in data mining , data analytics , and hypothesis testing in Python , enhances analytical frameworks and supports informed decision-making.

Understanding Hypothesis Testing- FAQs

What is hypothesis testing in data science.

In data science, hypothesis testing is used to validate assumptions or claims about data. It helps data scientists determine whether observed patterns are statistically significant or could have occurred by chance.

How does hypothesis testing work in machine learning?

In machine learning, hypothesis testing helps assess the effectiveness of models. For example, it can be used to compare the performance of different algorithms or to evaluate whether a new feature significantly improves a model’s accuracy.

What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

What is the difference between hypothesis testing and data mining?

Hypothesis testing focuses on evaluating specific claims or hypotheses about a dataset, while data mining involves exploring large datasets to discover patterns, relationships, or insights without predefined hypotheses.

How is hypothesis generation used in business analytics?

In business analytics , hypothesis generation involves formulating assumptions or predictions based on available data. These hypotheses can then be tested using statistical methods to inform decision-making and strategy.

What is the significance level in hypothesis testing?

The significance level, often denoted as alpha (α), is the threshold for deciding whether to reject the null hypothesis. Common significance levels are 0.05, 0.01, and 0.10, indicating the probability of making a Type I error in statistical hypothesis testing .

Similar Reads

• Data Science
• data-science

Please Login to comment...

Improve your coding skills with practice.

What kind of Experience do you want to share?