problem solving probability questions

Probability Questions with Solutions

Tutorial on finding the probability of an event. In what follows, S is the sample space of the experiment in question and E is the event of interest. n(S) is the number of elements in the sample space S and n(E) is the number of elements in the event E.

Questions and their Solutions

Answers to the above exercises, more references and links.

• Online Practice Tests

Probability Practice Problems

1. on a six-sided die, each side has a number between 1 and 6. what is the probability of throwing a 3 or a 4, 2. three coins are tossed up in the air, one at a time. what is the probability that two of them will land heads up and one will land tails up, 3. a two-digit number is chosen at random. what is the probability that the chosen number is a multiple of 7, 4. a bag contains 14 blue, 6 red, 12 green, and 8 purple buttons. 25 buttons are removed from the bag randomly. how many of the removed buttons were red if the chance of drawing a red button from the bag is now 1/3, 5. there are 6 blue marbles, 3 red marbles, and 5 yellow marbles in a bag. what is the probability of selecting a blue or red marble on the first draw, 6. using a six-sided die, carlin has rolled a six on each of 4 successive tosses. what is the probability of carlin rolling a six on the next toss, 7. a regular deck of cards has 52 cards. assuming that you do not replace the card you had drawn before the next draw, what is the probability of drawing three aces in a row.

• 1 in 132600

8. An MP3 player is set to play songs at random from the fifteen songs it contains in memory. Any song can be played at any time, even if it is repeated. There are 5 songs by Band A, 3 songs by Band B, 2 by Band C, and 5 by Band D. If the player has just played two songs in a row by Band D, what is the probability that the next song will also be by Band D?

• Not enough data to determine.

9. Referring again to the MP3 player described in Question 8, what is the probability that the next two songs will both be by Band B?

10. if a bag of balloons consists of 47 white balloons, 5 yellow balloons, and 10 black balloons, what is the approximate likelihood that a balloon chosen randomly from the bag will be black, 11. in a lottery game, there are 2 winners for every 100 tickets sold on average. if a man buys 10 tickets, what is the probability that he is a winner, answers and explanations.

1.  B:  On a six-sided die, the probability of throwing any number is 1 in 6. The probability of throwing a 3 or a 4 is double that, or 2 in 6. This can be simplified by dividing both 2 and 6 by 2.

Therefore, the probability of throwing either a 3 or 4 is 1 in 3.

2.  D:  Shown below is the sample space of possible outcomes for tossing three coins, one at a time. Since there is a possibility of two outcomes (heads or tails) for each coin, there is a total of 2*2*2=8 possible outcomes for the three coins altogether. Note that H represents heads and T represents tails:

HHH HHT HTT HTH TTT TTH THT THH

Notice that out of the 8 possible outcomes, only 3 of them (HHT, HTH, and THH) meet the desired condition that two coins land heads up and one coin lands tails up. Probability, by definition, is the number of desired outcomes divided by the number of possible outcomes. Therefore, the probability of two heads and one tail is 3/8, Choice D.

3.  E:  There are 90 two-digit numbers (all integers from 10 to 99). Of those, there are 13 multiples of 7: 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98.

4.  B:  Add the 14 blue, 6 red, 12 green, and 8 purple buttons to get a total of 40 buttons. If 25 buttons are removed, there are 15 buttons remaining in the bag. If the chance of drawing a red button is now 1/3, then 5 of the 15 buttons remaining must be red. The original total of red buttons was 6. So, one red button was removed.

5.  D:  Use this ratio for probability:

Probability = Number of Desired Outcomes

Number of Possible Outcomes

There are 6 blue marbles and 3 red marbles for a total of 9 desired outcomes. Add the total number of marbles to get the total number of possible outcomes, 14. The probability that a red or blue marble will be selected is 9/14.

6.  C:  The outcomes of previous rolls do not affect the outcomes of future rolls. There is one desired outcome and six possible outcomes. The probability of rolling a six on the fifth roll is 1/6, the same as the probability of rolling a six on any given individual roll.

7.  D:  The probability of getting three aces in a row is the product of the probabilities for each draw. For the first ace, that is 4 in 52 or 1 in 13; for the second, it is 3 in 51 or 1 in 27; and for the third, it is 2 in 50 or 1 in 25. So the overall probability,  P , is P=1/13*1/17*1/25=1/5,525

8.  B:  The probability of playing a song by a particular band is proportional to the number of songs by that band divided by the total number of songs, or 5/15=1/3 for B and D. The probability of playing any particular song is not affected by what has been played previously, since the choice is random and songs may be repeated.

9.  A:  Since 3 of the 15 songs are by Band B, the probability that any one song will be by that band is 3/15=1/5. The probability that the next two songs are by Band B is equal to the product of two probabilities, where each probability is that the next song is by Band B: 1/5*1/5=1/25 The same probability of 1/5 may be multiplied twice because whether or not the first song is by Band B has no impact on whether the second song is by Band B. They are independent events.

10.  B:  First, calculate the total number of balloons in the bag: 47 + 5 + 10 = 62.

Ten of these are black, so divide this number by 62. Then, multiply by 100 to express the probability as a percentage:

10 / 62 = 0.16

0.16 100 = 16%

11. C: First, simplify the winning rate. If there are 2 winners for every 100 tickets, there is 1 winner for every 50 tickets sold. This can be expressed as a probability of 1/50 or 0.02. In order to account for the (unlikely) scenarios of more than a single winning ticket, calculate the probability that none of the tickets win and then subtract that from 1. There is a probability of 49/50 that a given ticket will not win. For all ten to lose that would be (49/50)^(10) ≈ 0.817. Therefore, the probability that at least one ticket wins is 1 − 0.817 = 0.183 or about 18.3%

Solved Probability Problems

Solved probability problems and solutions are given here for a concept with clear understanding.

Students can get a fair idea on the probability questions which are provided with the detailed step-by-step answers to every question.

Solved probability problems with solutions :

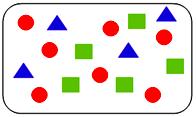
The graphic above shows a container with 4 blue triangles, 5 green squares and 7 red circles. A single object is drawn at random from the container.

Match the following events with the corresponding probabilities:

Number of blue triangles in a container = 4

Number of green squares = 5

Number of red circles = 7

Total number of objects = 4 + 5 + 7 = 16

(i) The objects is not a circle:

P(the object is a circle)

= Number of circles/Total number of objects

P(the object is not a circle)

= 1 - P(the object is a circle)

= (16 - 7)/16

(ii) The objects is a triangle:

P(the object is a triangle)

= Number of triangle/Total number of objects

(iii) The objects is not a triangle:

= Number of triangles/Total number of objects

P(the object is not a triangle)

= 1 - P(the object is a triangle)

= (16 - 4)/16

(iv) The objects is not a square:

P(the object is a square)

= Number of squares/Total number of objects

P(the object is not a square)

= 1 - P(the object is a square)

= (16 - 5)/16

(v) The objects is a circle:

(vi) The objects is a square:

Match the following events with the corresponding probabilities are shown below:

2. A single card is drawn at random from a standard deck of 52 playing cards.

Match each event with its probability.

Note: fractional probabilities have been reduced to lowest terms. Consider the ace as the highest card.

Total number of playing cards = 52

(i) The card is a diamond:

Number of diamonds in a deck of 52 cards = 13

P(the card is a diamond)

= Number of diamonds/Total number of playing cards

(ii) The card is a red king:

Number of red king in a deck of 52 cards = 2

P(the card is a red king)

= Number of red kings/Total number of playing cards

(iii) The card is a king or queen:

Number of kings in a deck of 52 cards = 4

Number of queens in a deck of 52 cards = 4

Total number of king or queen in a deck of 52 cards = 4 + 4 = 8

P(the card is a king or queen)

= Number of king or queen/Total number of playing cards

(iv) The card is either a red card or an ace:

Total number of red card or an ace in a deck of 52 cards = 28

P(the card is either a red card or an ace)

= Number of cards which is either a red card or an ace/Total number of playing cards

(v) The card is not a king:

P(the card is a king)

= Number of kings/Total number of playing cards

P(the card is not a king)

= 1 - P(the card is a king)

= (13 - 1)/13

(vi) The card is a five or lower:

Number of cards is a five or lower = 16

P(the card is a five or lower)

= Number of card is a five or lower/Total number of playing cards

(vii) The card is a king:

(viii) The card is black:

Number of black cards in a deck of 52 cards = 26

P(the card is black)

= Number of black cards/Total number of playing cards

3. A bag contains 3 red balls and 4 black balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is 

(ii) not black.

(i) Total number of possible outcomes = 3 + 4 = 7.

Number of favourable outcomes for the event E.

                              = Number of black balls = 4.

So, P(E) = \(\frac{\textrm{Number of Favourable Outcomes for the Event E}}{\textrm{Total Number of Possible Outcomes}}\)

             = \(\frac{4}{7}\).

(ii) The event of the ball being not black = \(\bar{E}\).

Hence, required probability = P(\(\bar{E}\))

                                        = 1 - P(E)

                                        = 1 - \(\frac{4}{7}\)

                                        = \(\frac{3}{7}\).

4. If the probability of Serena Williams a particular tennis match is 0.86, what is the probability of her losing the match?

Let E = the event of Serena Williams winning.

From the question, P(E) = 0.86.

Clearly, \(\bar{E}\) = the event of Serena Williams losing.

So, P(\(\bar{E}\)) = 1 - P(E) 

                            = 1 - 0.86

                            = 0.14

                            = \(\frac{14}{100}\)

                            = \(\frac{7}{50}\).

5. Find the probability of getting 53 Sunday in a leap year.

A leap year has 366 days. So, it has 52 weeks and 2 days.

So, 52 Sundays are assured. For 53 Sundays, one of the two remaining days must be a Sunday. 

For the remaining 2 days we can have

(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday).

So, total number of possible outcomes = 7.

Number of favourable outcomes for the event E = 2,   [namely, (Sunday, Monday), (Saturday, Sunday)].

So, by definition: P(E) = \(\frac{2}{7}\).

6. A lot of 24 bulbs contains 25% defective bulbs. A bulb is drawn at random from the lot. It is found to be not defective and it is not put back. Now, one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?

25% of 24 = \(\frac{25}{100}\) × 24 = 6.

So, there are 6 defective bulbs and 18 bulbs are not defective. 

After the first draw, the lot is left with 6 defective bulbs and 17 non-defective bulbs.

So, when the second bulb is drwn, the total number of possible outcomes = 23  (= 6+ 17).

Number of favourable outcomes for the event E = number of non-defective bulbs = 17.

So, the required probability = P(E) = (\frac{17}{23}\).

The examples can help the students to practice more questions on probability by following the concept provided in the solved probability problems.

• Probability

Random Experiments

Experimental Probability

Events in Probability

Empirical Probability

Coin Toss Probability

Probability of Tossing Two Coins

Probability of Tossing Three Coins

Complimentary Events

Mutually Exclusive Events

Mutually Non-Exclusive Events

Conditional Probability

Theoretical Probability

Odds and Probability

Playing Cards Probability

Probability and Playing Cards

Probability for Rolling Two Dice

Probability for Rolling Three Dice

• 9th Grade Math

From Solved Probability Problems to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Word Problems on H.C.F. and L.C.M. | Least Common Multiple | GCF Math

Jun 06, 24 06:27 PM

Worksheet on Word Problems on H.C.F. and L.C.M. |Highest Common Factor

Jun 06, 24 05:46 PM

Relationship between H.C.F. and L.C.M. |Highest Common Factor|Examples

Jun 05, 24 05:23 PM

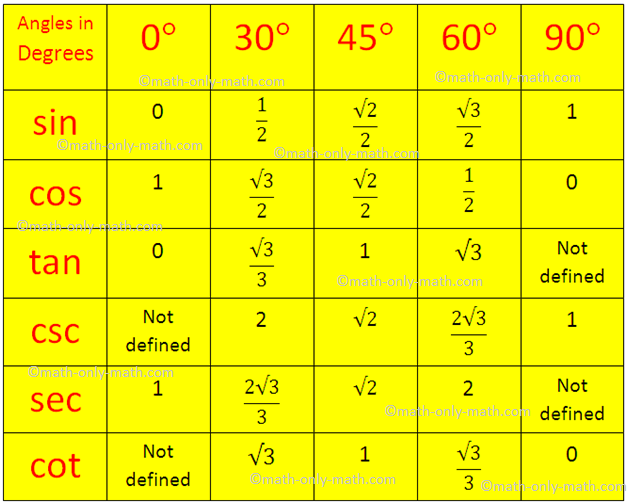
Trigonometrical Ratios Table | Trigonometric Standard Angles |Standard

Jun 05, 24 12:44 PM

Worksheet on L.C.M. | Least Common Multiple Worksheets |LCM Worksheets

Jun 04, 24 07:04 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

• Math Article

Probability Questions

The probability questions , with answers, are provided here for students to make them understand the concept in an easy way. The chapter Probability has been included in Class 9, 10, 11 and 12. Therefore, it is a very important chapter. The questions here will be provided, as per NCERT guidelines. Get Probability For Class 10 at BYJU’S.

The application of probability can be seen in Maths as well as in day to day life. It is necessary to learn the basics of this concept. The questions here will cover the basics as well as the hard level problems for all levels of students. Thus, students will be confident in solving problems based on it. Also, solving these probability problems will help them to participate in competitive exams, going further.

Definition: Probability is nothing but the possibility of an event occurring. For example, when a test is conducted, then the student can either get a pass or fail. It is a state of probability.

Also read: Probability

The probability of happening of an event E is a number P(E) such that:

0 ≤ P(E) ≤ 1

Probability Formula: If an event E occurs, then the empirical probability of an event to happen is:

P(E) = Number of trials in which Event happened/Total number of trials

The theoretical probability of an event E, P(E), is defined as:

P(E) = (Number of outcomes favourable to E)/(Number of all possible outcomes of the experiment)

Impossible event: The probability of an occurrence/event impossible to happen is 0. Such an event is called an impossible event.

Sure event: The probability of an event that is sure to occur is 1. Such an event is known as a sure event or a certain event.

Probability Questions & Answers

1. Two coins are tossed 500 times, and we get:

Two heads: 105 times

One head: 275 times

No head: 120 times

Find the probability of each event to occur.

Solution: Let us say the events of getting two heads, one head and no head by E 1 , E 2 and E 3 , respectively.

P(E 1 ) = 105/500 = 0.21

P(E 2 ) = 275/500 = 0.55

P(E 3 ) = 120/500 = 0.24

The Sum of probabilities of all elementary events of a random experiment is 1.

P(E 1 )+P(E 2 )+P(E 3 ) = 0.21+0.55+0.24 = 1

2. A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced. The table shows the results of 1000 cases.

If a tyre is bought from this company, what is the probability that :

(i) it has to be substituted before 4000 km is covered?

(ii) it will last more than 9000 km?

(iii) it has to be replaced after 4000 km and 14000 km is covered by it?

Solution: (i) Total number of trials = 1000.

The frequency of a tyre required to be replaced before covering 4000 km = 20

So, P(E 1 ) = 20/1000 = 0.02

(ii) The frequency that tyre will last more than 9000 km = 325 + 445 = 770

So, P(E 2 ) = 770/1000 = 0.77

(iii) The frequency that tyre requires replacement between 4000 km and 14000 km = 210 + 325 = 535.

So, P(E 3 ) = 535/1000 = 0.535

3. The percentage of marks obtained by a student in the monthly tests are given below:

Based on the above table, find the probability of students getting more than 70% marks in a test.

Solution: The total number of tests conducted is 5.

The number of tests when students obtained more than 70% marks = 3.

So, P(scoring more than 70% marks) = ⅗ = 0.6

4. One card is drawn from a deck of 52 cards, well-shuffled. Calculate the probability that the card will

(i) be an ace,

(ii) not be an ace.

Solution: Well-shuffling ensures equally likely outcomes.

(i) There are 4 aces in a deck.

Let E be the event the card drawn is ace.

The number of favourable outcomes to the event E = 4

The number of possible outcomes = 52

Therefore, P(E) = 4/52 = 1/13

(ii) Let F is the event of ‘card is not an ace’

The number of favourable outcomes to F = 52 – 4 = 48

Therefore, P(F) = 48/52 = 12/13

5. Two players, Sangeet and Rashmi, play a tennis match. The probability of Sangeet winning the match is 0.62. What is the probability that Rashmi will win the match?

Solution: Let S and R denote the events that Sangeeta wins the match and Reshma wins the match, respectively.

The probability of Sangeet to win = P(S) = 0.62

The probability of Rashmi to win = P(R) = 1 – P(S)

= 1 – 0.62 = 0.38

6. Two coins (a one rupee coin and a two rupee coin) are tossed once. Find a sample space.

Solution: Either Head(H) or Tail(T) can be the outcomes.

Heads on both coins = (H,H) = HH

Head on 1st coin and Tail on the 2nd coin = (H,T) = HT

Tail on 1st coin and Head on the 2nd coin = (T,H) = TH

Tail on both coins = (T,T) = TT

Therefore, the sample space is S = {HH, HT, TH, TT}

7. Consider the experiment in which a coin is tossed repeatedly until a head comes up. Describe the sample space.

Solution: In the random experiment where the head can appear on the 1st toss, or the 2nd toss, or the 3rd toss and so on till we get the head of the coin. Hence, the required sample space is :

S= {H, TH, TTH, TTTH, TTTTH,…}

8. Consider the experiment of rolling a die. Let A be the event ‘getting a prime number’, B be the event ‘getting an odd number’. Write the sets representing the events

(ii) A and B

(iii) A but not B

(iv) ‘not A’.

Solution: S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} and B = {1, 3, 5}

(i) A or B = A ∪ B = {1, 2, 3, 5}

(ii) A and B = A ∩ B = {3,5}

(iii) A but not B = A – B = {2}

(iv) not A = A′ = {1,4,6}

9. A coin is tossed three times, consider the following events.

P: ‘No head appears’,

Q: ‘Exactly one head appears’ and

R: ‘At Least two heads appear’.

Check whether they form a set of mutually exclusive and exhaustive events.

Solution: The sample space of the experiment is:

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and

Q = {HTT, THT, TTH},

R = {HHT, HTH, THH, HHH}

P ∪ Q ∪ R = {TTT, HTT, THT, TTH, HHT, HTH, THH, HHH} = S

Therefore, P, Q and R are exhaustive events.

P ∩ R = φ and

Therefore, the events are mutually exclusive.

Hence, P, Q and R form a set of mutually exclusive and exhaustive events.

10. If P(A) = 7/13, P(B) = 9/13 and P(A∩B) = 4/13, evaluate P(A|B).

Solution: P(A|B) = P(A∩B)/P(B) = (4/13)/(9/13) = 4/9.

Video Lesson

Probability important topics.

Probability Important Questions

Related Links

• Important Questions Class 9 Maths Chapter 15 Probability
• Important Questions Class 10 Maths Chapter 15 Probability
• Important Questions Class 11 Maths Chapter 16 Probability
• Important Questions Class 12 Maths Chapter 13 Probability

Practice Questions

Solve the following probability questions.

• Write the sample space for rolling two dice.
• If two coins are tossed simultaneously, what is the probability of getting exactly two heads?
• From a well-shuffled deck of 52 cards, what is the probability of getting a king?
• In a bag, there are 5 red balls and 7 black balls. What is the probability of getting a black ball?
• If the probability of an event happening is 0.7, then what is the probability of an event that will not happen?

Stay tuned with BYJU’S – The Learning App and learn all Maths-related concepts easily by exploring more videos.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Teach yourself statistics

How to Solve Probability Problems

You can solve many simple probability problems just by knowing two simple rules:

• The probability of any sample point can range from 0 to 1.
• The sum of probabilities of all sample points in a sample space is equal to 1.

The following sample problems show how to apply these rules to find (1) the probability of a sample point and (2) the probability of an event.

Probability of a Sample Point

The probability of a sample point is a measure of the likelihood that the sample point will occur.

Example 1 Suppose we conduct a simple statistical experiment . We flip a coin one time. The coin flip can have one of two equally-likely outcomes - heads or tails. Together, these outcomes represent the sample space of our experiment. Individually, each outcome represents a sample point in the sample space. What is the probability of each sample point?

Solution: The sum of probabilities of all the sample points must equal 1. And the probability of getting a head is equal to the probability of getting a tail. Therefore, the probability of each sample point (heads or tails) must be equal to 1/2.

Example 2 Let's repeat the experiment of Example 1, with a die instead of a coin. If we toss a fair die, what is the probability of each sample point?

Solution: For this experiment, the sample space consists of six sample points: {1, 2, 3, 4, 5, 6}. Each sample point has equal probability. And the sum of probabilities of all the sample points must equal 1. Therefore, the probability of each sample point must be equal to 1/6.

Probability of an Event

The probability of an event is a measure of the likelihood that the event will occur. By convention, statisticians have agreed on the following rules.

• The probability of any event can range from 0 to 1.
• The probability of event A is the sum of the probabilities of all the sample points in event A.
• The probability of event A is denoted by P(A).

Thus, if event A were very unlikely to occur, then P(A) would be close to 0. And if event A were very likely to occur, then P(A) would be close to 1.

Example 1 Suppose we draw a card from a deck of playing cards. What is the probability that we draw a spade?

Solution: The sample space of this experiment consists of 52 cards, and the probability of each sample point is 1/52. Since there are 13 spades in the deck, the probability of drawing a spade is

P(Spade) = (13)(1/52) = 1/4

Example 2 Suppose a coin is flipped 3 times. What is the probability of getting two tails and one head?

Solution: For this experiment, the sample space consists of 8 sample points.

S = {TTT, TTH, THT, THH, HTT, HTH, HHT, HHH}

Each sample point is equally likely to occur, so the probability of getting any particular sample point is 1/8. The event "getting two tails and one head" consists of the following subset of the sample space.

A = {TTH, THT, HTT}

The probability of Event A is the sum of the probabilities of the sample points in A. Therefore,

P(A) = 1/8 + 1/8 + 1/8 = 3/8

Browse Course Material

Course info, instructors.

• Dr. Jeremy Orloff
• Dr. Jennifer French Kamrin

Departments

• Mathematics

As Taught In

• Discrete Mathematics
• Probability and Statistics

Learning Resource Types

Introduction to probability and statistics, exams with solutions.

You are leaving MIT OpenCourseWare

Probability Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 7

• Statistics and probability FAQ
• Intro to theoretical probability
• Simple probability: yellow marble
• Simple probability: non-blue marble

Simple probability

• Experimental probability
• Intuitive sense of probabilities
• Comparing probabilities

• Your answer should be
• an integer, like 6 ‍  
• an exact decimal, like 0.75 ‍  
• a proper fraction, like 1 / 2 ‍   or 6 / 10 ‍  
• an improper fraction, like 10 / 7 ‍   or 14 / 8 ‍  
• a mixed number, like 1   3 / 4 ‍  
• a percent, like 12.34 % ‍  

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Search IntMath
• Math interactives
• About (site info)
• Uses of Trignometry
• ASCIIMath input, KaTeX output
• ASCIIMath input, LaTeX and KaTeX output
• Send Math in emails
• Syntax for ASCIIMathML
• Math Display Experiments
• Scientific Notebook
• Math Problem Solver

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Probability Problem Solver

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of artificial intelligence large language models to parse and generate natural language answers. This creates a math problem solver that's more accurate than ChatGPT, more flexible than a math calculator, and provides answers faster than a human tutor.

Sign up for free here .

Problem Solver Subjects

Our math problem solver that lets you input a wide variety of probability math problems and it will provide a step by step answer. This math solver excels at math word problems as well as a wide range of math subjects.

• Math Word Problems
• Pre-Algebra
• Geometry Graphing
• Trigonometry
• Precalculus
• Finite Math
• Linear Algebra

Here are example math problems within each subject that can be input into the calculator and solved. This list is constanstly growing as functionality is added to the calculator.

Basic Math Solutions

Below are examples of basic math problems that can be solved.

• Long Arithmetic
• Rational Numbers
• Operations with Fractions
• Ratios, Proportions, Percents
• Measurement, Area, and Volume
• Factors, Fractions, and Exponents
• Unit Conversions
• Data Measurement and Statistics
• Points and Line Segments

Math Word Problem Solutions

Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.

Word Problem: Rachel has 17 apples. She gives some to Sarah. Sarah now has 8 apples. How many apples did Rachel give her?

Simplified Equation: 17 - x = 8

Word Problem: Rhonda has 12 marbles more than Douglas. Douglas has 6 marbles more than Bertha. Rhonda has twice as many marbles as Bertha has. How many marbles does Douglas have?

Variables: Rhonda's marbles is represented by (r), Douglas' marbles is represented by (d) and Bertha's marbles is represented by (b)

Simplified Equation: {r = d + 12, d = b + 6, r = 2 �� b}

Word Problem: if there are 40 cookies all together and Angela takes 10 and Brett takes 5 how many are left?

Simplified: 40 - 10 - 5

Pre-Algebra Solutions

Below are examples of Pre-Algebra math problems that can be solved.

• Variables, Expressions, and Integers
• Simplifying and Evaluating Expressions
• Solving Equations
• Multi-Step Equations and Inequalities
• Ratios, Proportions, and Percents
• Linear Equations and Inequalities

Algebra Solutions

Below are examples of Algebra math problems that can be solved.

• Algebra Concepts and Expressions
• Points, Lines, and Line Segments
• Simplifying Polynomials
• Factoring Polynomials
• Linear Equations
• Absolute Value Expressions and Equations
• Radical Expressions and Equations
• Systems of Equations
• Quadratic Equations
• Inequalities
• Complex Numbers and Vector Analysis
• Logarithmic Expressions and Equations
• Exponential Expressions and Equations
• Conic Sections
• Vector Spaces
• 3d Coordinate System
• Eigenvalues and Eigenvectors
• Linear Transformations
• Number Sets
• Analytic Geometry

Trigonometry Solutions

Below are examples of Trigonometry math problems that can be solved.

• Algebra Concepts and Expressions Review
• Right Triangle Trigonometry
• Radian Measure and Circular Functions
• Graphing Trigonometric Functions
• Simplifying Trigonometric Expressions
• Verifying Trigonometric Identities
• Solving Trigonometric Equations
• Complex Numbers
• Analytic Geometry in Polar Coordinates
• Exponential and Logarithmic Functions
• Vector Arithmetic

Precalculus Solutions

Below are examples of Precalculus math problems that can be solved.

• Operations on Functions
• Rational Expressions and Equations
• Polynomial and Rational Functions
• Analytic Trigonometry
• Sequences and Series
• Analytic Geometry in Rectangular Coordinates
• Limits and an Introduction to Calculus

Calculus Solutions

Below are examples of Calculus math problems that can be solved.

• Evaluating Limits
• Derivatives
• Applications of Differentiation
• Applications of Integration
• Techniques of Integration
• Parametric Equations and Polar Coordinates
• Differential Equations

Statistics Solutions

Below are examples of Statistics problems that can be solved.

• Algebra Review
• Average Descriptive Statistics
• Dispersion Statistics
• Probability
• Probability Distributions
• Frequency Distribution
• Normal Distributions
• t-Distributions
• Hypothesis Testing
• Estimation and Sample Size
• Correlation and Regression

Finite Math Solutions

Below are examples of Finite Math problems that can be solved.

• Polynomials and Expressions
• Equations and Inequalities
• Linear Functions and Points
• Systems of Linear Equations
• Mathematics of Finance
• Statistical Distributions

Linear Algebra Solutions

Below are examples of Linear Algebra math problems that can be solved.

• Introduction to Matrices
• Linear Independence and Combinations

Chemistry Solutions

Below are examples of Chemistry problems that can be solved.

• Unit Conversion
• Atomic Structure
• Molecules and Compounds
• Chemical Equations and Reactions
• Behavior of Gases
• Solutions and Concentrations

Physics Solutions

Below are examples of Physics math problems that can be solved.

• Static Equilibrium
• Dynamic Equilibrium
• Kinematics Equations
• Electricity
• Thermodymanics

Geometry Graphing Solutions

Below are examples of Geometry and graphing math problems that can be solved.

• Step By Step Graphing
• Linear Equations and Functions
• Polar Equations

Looking for the old Mathway Calculator? We've moved it to here .

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

FREE GCSE Maths Resources

40+ GCSE maths papers (foundation & higher), 200+ worksheets, 15,000+ practice questions and more!

15 Probability Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included

Beki Christian

Probability questions and probability problems require students to work out how likely it is that something is to happen. Probabilities can be described using words or numbers. Probabilities range from 0 to 1 and can be written as fractions, decimals or percentages.

Here you’ll find a selection of probability questions of varying difficulty showing the variety you are likely to encounter in KS3 and KS4 including several GCSE exam style questions.

What are some real life examples of probability?

How to calculate probabilities, year 7 probability questions, year 8 probability questions, year 9 probability questions, year 10 probability questions, gcse foundation probability questions, gcse higher probability questions, looking for more probability questions and resources, looking for more ks3 and ks4 maths questions.

FREE GCSE MATHS REVISION RESOURCES FOR SCHOOLS

As part of the Third Space Learning offer to schools, the personalised online GCSE maths tuition can be supplemented by hundreds of free GCSE maths revision resources from the secondary maths resources library including:

• GCSE maths past papers
• GCSE maths worksheets
• GCSE maths questions
• GCSE maths topic list

The more likely something is to happen, the higher its probability. We think about probabilities all the time. For example, you may have seen that there is a 20% chance of rain on a certain day or thought about how likely you are to roll a 6 when playing a game, or to win in a raffle when you buy a ticket.

The probability of something happening is given by:

We can also use the following formulae to help us calculate probabilities and solve problems:

• Probability of something not occuring = 1 – probability of if occurring P(not\;A) = 1 - P(A)
• For mutually exclusive events: Probability of event A OR event B occurring = Probability of event A + Probability of event B P(A\;or\;B) = P(A)+P(B)
• For independent events: Probability of event A AND event B occurring = Probability of event A times probability of event B P(A\;and\;B) = P(A) × P(B)

Download this 15 Probability Questions And Practice Problems (KS3 & KS4) Worksheet

Help your students prepare for their Maths GSCE with this free Probability worksheet of 15 multiple choice questions and answers.

KS3 probability questions

In KS3 probability questions introduce the idea of the probability scale and the fact that probabilities sum to one. We look at theoretical and experimental probability as well as learning about sample space diagrams and venn diagrams.

1. Which number could be added to this spinner to make it more likely that the spinner will land on an odd number than a prime number?

Currently there are two odd numbers and two prime numbers so the chances of landing on an odd number or a prime number are the same. By adding 3, 5 or 11 you would be adding one prime number and one odd number so the chances would remain equal.

By adding 9 you would be adding an odd number but not a prime number. There would be three odd numbers and two prime numbers so the spinner would be more likely to land on an odd number than a prime number.

2. Ifan rolls a fair dice, with sides labelled A, B, C, D, E and F. What is the probability that the dice lands on a vowel?

A and E are vowels so there are 2 outcomes that are vowels out of 6 outcomes altogether.

Therefore the probability is   \frac{2}{6} which can be simplified to \frac{1}{3} .

3. Max tested a coin to see whether it was fair. The table shows the results of his coin toss experiment:

Heads          Tails

    26                  41

What is the relative frequency of the coin landing on heads?

Max tossed the coin 67 times and it landed on heads 26 times.

\text{Relative frequency (experimental probability) } = \frac{\text{number of successful trials}}{\text{total number of trials}} = \frac{26}{67}

4. Grace rolled two dice. She then did something with the two numbers shown. Here is a sample space diagram showing all the possible outcomes:

What did Grace do with the two numbers shown on the dice?

Add them together

Subtract the number on dice 2 from the number on dice 1

Multiply them

Subtract the smaller number from the bigger number

For each pair of numbers, Grace subtracted the smaller number from the bigger number.

For example, if she rolled a 2 and a 5, she did 5 − 2 = 3.

5. Alice has some red balls and some blue balls in a bag. Altogether she has 25 balls. Alice picks one ball from the bag. The probability that Alice picks a red ball is x and the probability that Alice picks a blue ball is 4x. Work out how many blue balls are in the bag.

Since the probability of mutually exclusive events add to 1:  

\begin{aligned} x+4x&=1\\\\ 5x&=1\\\\ x&=\frac{1}{5} \end{aligned}

\frac{1}{5} of the balls are red and \frac{4}{5} of the balls are blue.

6. Arthur asked the students in his class whether they like maths and whether they like science. He recorded his results in the venn diagram below.

How many students don’t like science?

We need to look at the numbers that are not in the ‘Like science’ circle. In this case it is 9 + 7 = 16.

KS4 probability questions

In KS4 probability questions involve more problem solving to make predictions about the probability of an event. We also learn about probability tree diagrams, which can be used to represent multiple events, and conditional probability.

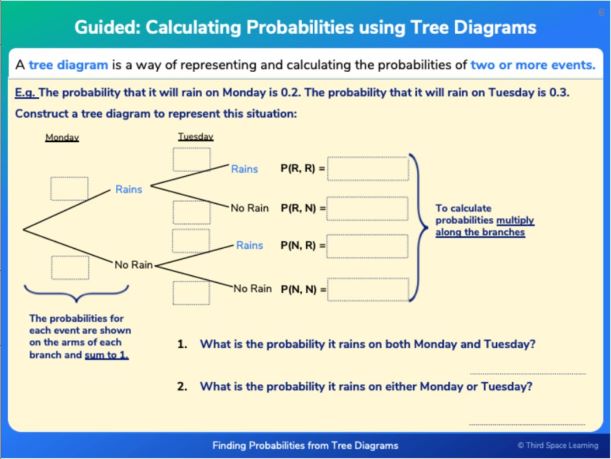
7. A restaurant offers the following options:

Starter – soup or salad

Main – chicken, fish or vegetarian

Dessert – ice cream or cake

How many possible different combinations of starter, main and dessert are there?

The number of different combinations is 2 × 3 × 2 = 12.

8. There are 18 girls and 12 boys in a class. \frac{2}{9} of the girls and \frac{1}{4} of the boys walk to school. One of the students who walks to school is chosen at random. Find the probability that the student is a boy. 

First we need to work out how many students walk to school:

\frac{2}{9} \text{ of } 18 = 4

\frac{1}{4} \text{ of } 12 = 3

7 students walk to school. 4 are girls and 3 are boys. So the probability the student is a boy is \frac{3}{7} .

9. Rachel flips a biased coin. The probability that she gets two heads is 0.16. What is the probability that she gets two tails?

We have been given the probability of getting two heads. We need to calculate the probability of getting a head on each flip.

Let’s call the probability of getting a head p.

The probability p, of getting a head AND getting another head is 0.16.

Therefore to find p:

The probability of getting a head is 0.4 so the probability of getting a tail is 0.6.

The probability of getting two tails is 0.6 × 0.6 = 0.36 .

10. I have a big tub of jelly beans. The probability of picking each different colour of jelly bean is shown below:

If I were to pick 60 jelly beans from the tub, how many orange jelly beans would I expect to pick?

First we need to calculate the probability of picking an orange. Probabilities sum to 1 so 1 − (0.2 + 0.15 + 0.1 + 0.3) = 0.25.

The probability of picking an orange is 0.25.

The number of times I would expect to pick an orange jelly bean is 0.25 × 60 = 15 .

11. Dexter runs a game at a fair. To play the game, you must roll a dice and pick a card from a deck of cards.

To win the game you must roll an odd number and pick a picture card. The game can be represented by the tree diagram below.

Dexter charges players £1 to play and gives £3 to any winners. If 260 people play the game, how much profit would Dexter expect to make?

Completing the tree diagram:

Probability of winning is \frac{1}{2} \times \frac{4}{13} = \frac{4}{26}

If 260 play the game, Dexter would receive £260.

The expected number of winners would be \frac{4}{26} \times 260 = 40

Dexter would need to give away 40 × £3 = £120 .

Therefore Dexter’s profit would be £260 − £120 = £140.

12. A coin is tossed three times. Work out the probability of getting two heads and one tail. 

There are three ways of getting two heads and one tail: HHT, HTH or THH.

The probability of each is \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8} 

Therefore the total probability is \frac{1}{8} +\frac{1}{8} + \frac{1}{8} = \frac{3}{8}

13. 200 people were asked about which athletics event they thought was the most exciting to watch. The results are shown in the table below.

A person is chosen at random. Given that that person chose 100m, what is the probability that the person was female?

Since we know that the person chose 100m, we need to include the people in that column only.

In total 88 people chose 100m so the probability the person was female is \frac{32}{88}   .

14.   Sam asked 50 people whether they like vegetable pizza or pepperoni pizza.

37 people like vegetable pizza. 

25 people like both. 

3 people like neither.

Sam picked one of the 50 people at random. Given that the person he chose likes pepperoni pizza, find the probability that they don’t like vegetable pizza.

We need to draw a venn diagram to work this out.

We start by putting the 25 who like both in the middle section. The 37 people who like vegetable pizza includes the 25 who like both, so 12 more people must like vegetable pizza. 3 don’t like either. We have 50 – 12 – 25 – 3 = 10 people left so this is the number that must like only pepperoni.

There are 35 people altogether who like pepperoni pizza. Of these, 10 do not like vegetable pizza. The probability is   \frac{10}{35} .

15. There are 12 marbles in a bag. There are n red marbles and the rest are blue marbles. Nico takes 2 marbles from the bag. Write an expression involving n for the probability that Nico takes one red marble and one blue marble.

We need to think about this using a tree diagram. If there are 12 marbles altogether and n are red then 12-n are blue.

To get one red and one blue, Nico could choose red then blue or blue then red so the probability is:

Third Space Learning’s free GCSE maths resource library contains detailed lessons with step-by-step instructions on how to solve ratio problems, as well as worksheets with ratio and proportion practice questions and more GCSE exam questions.

Take a look at the probability lessons today – more are added every week.

• 25 GCSE maths questions
• 15 Ratio questions
• 15 Algebra questions
• 15 Trigonometry questions
• 15 Simultaneous equations questions
• 15 Venn diagram questions
• 15 Pythagoras theorem questions
• Long division questions

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist GCSE maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn about the GCSE revision programme or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

15 Pythagoras Theorem Questions And Practice Problems (KS3 & KS4)

Fluent In Five: A Daily Arithmetic Resource For Secondary

15 Venn Diagram Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included

15 Simultaneous Equations Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included

FREE GCSE Maths Practice Papers (Edexcel, AQA & OCR)

8 sets of free exam papers written by maths teachers and examiners.

Each set of exam papers contains the three papers that your students will expect to find in their GCSE mathematics exam.

Privacy Overview

Reset password New user? Sign up

Existing user? Log in

• Number Theory
• Probability
• Everyday Math
• Classical Mechanics
• Electricity and Magnetism
• Computer Science
• Quantitative Finance

Take a guided, problem-solving based approach to learning Probability. These compilations provide unique perspectives and applications you won't find anywhere else.

Probability Fundamentals

What's inside.

• Introduction
• Starting with Probability
• Principles of Probability
• Roll the Dice
• Fairness and Expected Value

Perplexing Probability

• Survive This Chapter
• Brain-Warping Probability
• Crazy Mad Dice

Casino Probability

• Casino Craps

Community Wiki

Browse through thousands of Probability wikis written by our community of experts.

• Rule of Sum
• Counting Integers in a Range
• Rule of Product
• Rule of Sum and Rule of Product Problem Solving
• Counting Shapes
• Discrete Mathematics
• Set Complement
• Permutations
• Permutations with Repetition
• Permutations With Restriction
• Combinatorics
• Combinations
• Rectangular Grid Walk

Sets and Partitions

• Sets - Elements
• Sets - Subsets
• Classical Sets
• Cardinality
• Partially Ordered Sets
• Ordinal Numbers
• Venn Diagram
• Union and Intersection
• Principle of Inclusion and Exclusion (PIE)
• Double Counting
• Derangements
• Bijection, Injection, And Surjection
• Bijective Functions
• Burnside's Lemma
• Pigeonhole Principle
• Ramsey Theory
• Dilworth's Theorem
• Distinct Objects into Distinct Bins
• Distinct Objects into Identical Bins
• Identical Objects into Distinct Bins
• Identical Objects into Identical Bins
• Partition of an Integer
• Mean (Average)
• Interquartile Range (IQR)
• Understanding Data - Problem Solving
• Data Presentation - Tables
• Data Presentation - Bar Charts
• Data Presentation - Pie Charts
• Data Presentation - Dot Diagram
• Data Presentation - Histogram
• Data Presentation - Stem-leaf plot
• Uniform Probability (by Outcomes)
• Probability - Rule of Sum
• Probability - Rule of Product
• Probability - By Complement
• Probability - Problem Solving
• Math of Poker - Basics
• Conditional Probability
• Probability - Independent events
• Probabilistic Principle of Inclusion and Exclusion
• Bayes' Theorem and Conditional Probability
• Conditional Probability Distribution
• Monty Hall Problem
• Bayesian Theory in Science and Math
• Poker Strategy
• Expected Value
• Linearity of Expectation
• Law of Iterated Expectation
• Coupon Collector Problem
• Standard Deviation
• Geometric Probability

Random Variables

• Discrete Random Variables - Definition
• Discrete Random Variables - Probability Density Function (PDF)
• Discrete Random Variables - Cumulative Distribution Function
• Discrete Random Variables - Joint Probability Distribution
• Discrete Random Variables - Indicator Variables
• Continuous Random Variables - Definition
• Continuous Random Variables - Probability Density Function (PDF)
• Continuous Random Variables - Cumulative Distribution Function
• Continuous Random Variables - Joint Probability Distribution
• Bernoulli Distribution
• Binomial Distribution
• Geometric Distribution
• Poisson Distribution
• Hypergeometric Distribution
• Continuous Probability Distributions - Uniform Distribution
• Normal Distribution
• Exponential Distribution
• Log-normal Distribution
• Multivariate Normal Distribution
• Sampling (Statistics)
• Chi-Squared Test
• Maximum Likelihood Estimation (MLE)
• Inverse Transform Sampling
• Statistical Significance
• Markov Chains
• Stationary Distributions of Markov Chains
• Transience and Recurrence of Markov Chains
• Ergodic Markov Chains
• Absorbing Markov Chains
• Binomial Theorem
• Binomial Coefficient
• Pascal's Triangle
• Negative Binomial Theorem
• Fractional Binomial Theorem
• Multinomial Coefficients
• Multinomial Theorem
• Recurrence Relations
• Minkowski Dimension
• Fibonacci Sequence
• Linear Recurrence Relations

Advanced Discrete

• Combinatorial Games - Definition
• Combinatorial Games - Winning Positions
• Sprague Grundy Theorem
• Dots and Boxes
• Fair Division
• Axiom of Determinacy
• Conjectures
• Construction
• Extremal Principle
• Invariant Principle
• Vandermonde's Identity
• Hockey Stick Identity
• Graph Theory
• Eulerian Path
• Hamiltonian Path
• Four Color Theorem
• Graph Coloring and Chromatic Numbers
• Hall's Marriage Theorem
• Applications of Hall's Marriage Theorem
• Art Gallery Problem
• Wiki Collaboration Graph
• Combinatorial Optimization
• Group actions
• Generating Functions
• Manipulating Generating Functions
• Coloring (Parity Arguments)

Problem Loading...

Note Loading...

Set Loading...

Probability Word Problem Worksheet

Related Topics & Worksheets: Probability Worksheet 2 Complementary Probability Worksheet

Objective: I know how to solve probability word problems.

The following are more probability problems for you to practice.

Read the lesson on probability problems for more information and examples.

Work out the following. When necessary, give your answer in fractions eg. 2/5

• In a class of 40 students, 8 are in the drama club and 12 are in the art club. If a student is selected at random, what is the probability that the selected student is: a) in the drama club? b) in the art club?
• A bag contains 50 marbles, 28 red ones and 22 blue ones. A marble is picked at random from the bag. What is the probability of picking: a) a red marble? b) a blue marble? c) a red marble after a blue marble had been picked first.
• A two-digit number is written at random. Determine the probability that the number will be: a) an odd number. b) larger than 75. c) a multiple of 5. d) an even number smaller than 40.
• In a group of 30 students, there are 14 girls and 4 of them can speak French. 6 of the 16 boys can speak French. If a student is selected randomly from the group, find the probability that the selected student: a) can speak French. b) is a boy. c) is a girl who can speak French.

We hope that the free math worksheets have been helpful. We encourage parents and teachers to select the topics according to the needs of the child. For more difficult questions, the child may be encouraged to work out the problem on a piece of paper before entering the solution. We hope that the kids will also love the fun stuff and puzzles.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Probability Problems? (+FREE Worksheet!)

Do you want to know how to solve Probability Problems? Here you learn how to solve probability word problems.

Related Topics

• How to Interpret Histogram
• How to Interpret Pie Graphs
• How to Solve Permutations and Combinations
• How to Find Mean, Median, Mode, and Range of the Given Data

Step by step guide to solve Probability Problems

• Probability is the likelihood of something happening in the future. It is expressed as a number between zero (can never happen) to \(1\) (will always happen).
• Probability can be expressed as a fraction, a decimal, or a percent.
• To solve a probability problem identify the event, find the number of outcomes of the event, then use probability law: \(\frac{number\ of \ favorable \ outcome}{total \ number \ of \ possible \ outcomes}\)

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Probability problems – example 1:.

If there are \(8\) red balls and \(12\) blue balls in a basket, what is the probability that John will pick out a red ball from the basket?

There are \(8\) red balls and \(20\) a total number of balls. Therefore, the probability that John will pick out a red ball from the basket is \(8\) out of \(20\) or \(\frac{8}{8+12}=\frac{8}{20}=\frac{2}{5}\).

Probability Problems – Example 2:

A bag contains \(18\) balls: two green, five black, eight blue, a brown, a red, and one white. If \(17\) balls are removed from the bag at random, what is the probability that a brown ball has been removed?

If \(17\) balls are removed from the bag at random, there will be one ball in the bag. The probability of choosing a brown ball is \(1\) out of \(18\). Therefore, the probability of not choosing a brown ball is \(17\) out of \(18\) and the probability of having not a brown ball after removing \(17\) balls is the same.

Exercises for Solving Probability Problems

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

• A number is chosen at random from \(1\) to \(10\). Find the probability of selecting a \(4\) or smaller.
• A number is chosen at random from \(1\) to \(50\). Find the probability of selecting multiples of \(10\).
• A number is chosen at random from \(1\) to \(10\). Find the probability of selecting of \(4\) and factors of \(6\).
• A number is chosen at random from \(1\) to \(10\). Find the probability of selecting a multiple of \(3\).
• A number is chosen at random from \(1\) to \(50\). Find the probability of selecting prime numbers.
• A number is chosen at random from \(1\) to \(25\). Find the probability of not selecting a composite number.

Download Probability Problems Worksheet

• \(\color{blue}{\frac{2}{5}}\)
• \(\color{blue}{\frac{1}{10}}\)
• \(\color{blue}{\frac{1}{2}}\)
• \(\color{blue}{\frac{3}{10}}\)
• \(\color{blue}{\frac{9}{25}}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• How to Solve Logarithmic Equations? (+FREE Worksheet!)
• Definition and Properties of Inverse Trigonometric Functions
• 5th Grade KAP Math Worksheets: FREE & Printable
• 4th Grade WVGSA Math Worksheets: FREE & Printable
• 3rd Grade ACT Aspire Math Worksheets: FREE & Printable
• The Secret Decoder Ring of Proportional Relationships: How to Find The Constant of Proportionality
• 8th Grade Georgia Milestones Assessment System Math FREE Sample Practice Questions
• 10 Most Common 8th Grade FSA Math Questions
• How to Match Word Problems with the One-Step Equations?

What people say about "How to Solve Probability Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Number Line

• A\:fair\:coin\:is\:tossed\:four\:times\:what\:is\:the\:probability\:of\:obtaining\:at\:least\:three\:heads
• What\:is\:the\:probability\:of\:rolling\:2\:standard\:dice\:which\:sum\:to\:11
• One\:card\:is\:selected\:at\:random\:from\:a\:deck\:of\:cards.\:Determine\:the\:probability\:that\:the\:card\:selected\:is\:a\:9?

probability-problems-calculator

• Middle School Math Solutions – Inequalities Calculator Next up in our Getting Started maths solutions series is help with another middle school algebra topic - solving...

Please add a message.

Message received. Thanks for the feedback.

• Testimonial
• Web Stories

Learning Home

Not Now! Will rate later

• Probability: Solved Examples

• Probability: Concepts & Tricks
• Probability Practice Questions: Level 01
• Probability Practice Questions: Level 02

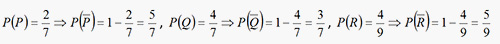
Most Popular Articles - PS

Time and Work Concepts

Time and Work Formula and Solved Problems

Time and Work Problems (Easy)

Time and Work Problems (Difficult)

Problems on Ages Practice Problems : Level 02

Chain Rule : Theory & Concepts

Chain Rule Solved Examples

Chain Rule Practice Problems: Level 01

Chain Rule Practice Problems : Level 02

Problems on Numbers System : Level 02

Download our app.

• Learn on-the-go
• Unlimited Prep Resources
• Better Learning Experience
• Personalized Guidance

Get More Out of Your Exam Preparation - Try Our App!

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes

Probability Questions

• Aptitude | Probability | Question 2
• Aptitude | Probability | Question 9
• Aptitude | Probability | Question 3
• Aptitude | Probability | Question 7
• Aptitude | Probability | Question 8
• Aptitude | Probability | Question 5
• Aptitude | Probability | Question 1
• Aptitude | Probability | Question 4
• Aptitude | Probability | Question 6
• Aptitude | Probability | Question 10
• Dice | Probability Quiz | Question 7
• Dice | Probability Quiz | Question 6
• Dice | Probability Quiz | Question 5
• Dice | Probability Quiz | Question 4
• Dice | Probability Quiz | Question 2
• Dice | Probability Quiz | Question 3
• Dice | Probability Quiz | Question 1
• Dice | Probability Quiz | Question 10

Probability is an important chapter for the students of Class 9, 10, 11, and 12. The Probability Questions, with their answers included in this article, will help you understand the basic concepts and formula. These questions cover concepts like Sample Space, Events, Coin Probability, etc. Solving these problems will improve your understanding and problem-solving skills in probability.

Important Formulas on Probability

Probability of an Event :

P ( E ) = Number of favorable outcomes​ / Total number of outcomes

Addition Rule :

For any two events A and B,

P(A ⋃ B) = P(A) + P(B) – P(A ⋂ B)

If A and B are mutually exclusive (disjoint),   

P(A ⋃ B) = P(A) + P(B)

Multiplication Rule :

P(A ⋂ B) = P(A) · P(B | A)

If A and B are independent,

P(A ⋂ B) = P(A) · P(B)

Conditional Probability :

P(B | A) = P(A ⋂ B) / P(A)

Bayes’ Theorem :

P(A | B) = [P(B | A) · P(A)] / P(B)

Total Probability Rule :

If B1, B2, …, Bn are mutually exclusive and exhaustive events,

P(A) = P(A ⋂ B1) + P(A ⋂ B2) + … + P(A ⋂ Bn)

Probability Questions with Solutions

Question 1: a fair six-sided die is rolled. what is the probability of rolling a number greater than 4.

There are 2 favorable outcomes (5 and 6) out of 6 possible outcomes. Probability = Number of favorable outcomes / Total number of outcomes. = 2 / 6 = 1 / 3 ≈ 0.3333 or 33.33%.

Question 2: A jar contains 3 red, 4 blue, and 5 green marbles. What is the probability of randomly drawing a red marble?

Total marbles = 3 (red) + 4 (blue) + 5 (green) = 12. Probability of drawing a red marble = Number of red marbles / Total number of marbles. = 3 / 12 = 1 / 4 = 0.25 or 25%.

Question 3: From a deck of 52 cards, what is the probability of drawing an ace or a king?

There are 4 aces and 4 kings in the deck. Total favorable outcomes = 4 (aces) + 4 (kings) = 8. Probability = Number of favorable outcomes / Total number of outcomes. = 8 / 52 = 2 / 13 ≈ 0.1538 or 15.38%.

Question 4: A bag contains 10 balls: 6 black and 4 white. Two balls are drawn at random. What is the probability that both are black?

Probability of first ball being black = 6/10. After drawing one black ball, there are 5 black balls left and 9 balls in total. Probability of second ball being black = 5/9. Total probability = (6/10) × (5/9) = 30/90 = 1/3 ≈ 0.3333 or 33.33%.

Question 5: What is the probability of getting an even number when a fair six-sided die is rolled?

There are 3 even numbers on a die (2, 4, 6). Total outcomes = 6. Probability of rolling an even number = Number of even numbers / Total outcomes. = 3 / 6 = 1 / 2 = 0.5 or 50%.

Question 6: A box contains 2 red, 3 green, and 5 blue pens. If one pen is chosen at random, what is the probability it is not blue?

Total pens = 2 (red) + 3 (green) + 5 (blue) = 10. Number of non-blue pens = 2 (red) + 3 (green) = 5. Probability of not choosing a blue pen = Number of non-blue pens / Total pens. = 5 / 10 = 1 / 2 = 0.5 or 50%.

Question 7: What is the probability of flipping a coin three times and getting at least one head?

Probability of getting no heads (all tails) = (1/2)³ = 1/8. Probability of getting at least one head = 1 – Probability of getting no heads. = 1 – 1/8 = 7/8 = 0.875 or 87.5%.

Question 8: In a class of 20 students, 12 are girls. What is the probability of randomly selecting a boy?

Total students = 20. Number of boys = Total students – Number of girls = 20 – 12 = 8. Probability of selecting a boy = Number of boys / Total students. = 8 / 20 = 2 / 5 = 0.4 or 40%.

Question 9: A bag contains 5 red, 7 blue, and 8 green balls. Two balls are drawn without replacement. What is the probability that both balls are red?

Probability of first ball being red = 5/20. After drawing one red ball, there are 4 red balls left and 19 balls in total. Probability of second ball being red = 4/19. Total probability = (5/20) × (4/19) = 20/380 = 1/19 ≈ 0.0526 or 5.26%.

Question 10: From a standard deck of 52 cards, what is the probability of drawing a heart or a queen?

Total hearts = 13, Total queens = 4. Since one of the queens is also a heart, there are 3 queens that aren’t hearts. Total favorable outcomes = 13 (hearts) + 3 (other queens) = 16. Probability = Number of favorable outcomes / Total outcomes. = 16 / 52 = 4 / 13 ≈ 0.3077 or 30.77%.

Related Links:

Probability in Maths Events in Probability Coin Toss Probability

Question 11: A bag contains 4 red, 6 blue, and 5 green marbles. If two marbles are drawn randomly, what is the probability that both are the same color?

Total marbles = 4 (red) + 6 (blue) + 5 (green) = 15. Probability of drawing 2 red marbles = (4/15) × (3/14). Probability of drawing 2 blue marbles = (6/15) × (5/14). Probability of drawing 2 green marbles = (5/15) × (4/14). Total probability = Sum of the above probabilities. = (4/15) × (3/14) + (6/15) × (5/14) + (5/15) × (4/14).

Question 12: A spinner with numbers 1 to 5 is spun twice. What is the probability that the sum of the two spins is 6?

The possible outcomes that sum to 6 are: (1,5), (2,4), (3,3), (4,2), and (5,1). Total outcomes when spinning twice = 5 × 5 = 25. Probability = Number of favorable outcomes / Total outcomes. = 5 / 25 = 1 / 5 = 0.2 or 20%.

Question 13: What is the probability of not drawing a face card (Jack, Queen, King) from a standard deck of 52 cards?

Total face cards in the deck = 12 (4 Jacks, 4 Queens, 4 Kings). Total non-face cards = 52 – 12 = 40. Probability of not drawing a face card = Number of non-face cards / Total cards. = 40 / 52 = 10 / 13 ≈ 0.7692 or 76.92%.

Question 14: A jar contains 10 balls, of which 3 are red and 7 are black. If one ball is drawn and then replaced, and a second ball is drawn, what is the probability that both balls are red?

Probability of drawing a red ball and replacing it = 3/10. Since the ball is replaced, the probability of drawing a red ball again = 3/10. Total probability = (3/10) × (3/10) = 9/100 = 0.09 or 9%.

Question 15: In a lottery, there are 100 tickets numbered from 1 to 100. What is the probability that a ticket drawn at random has a number which is a multiple of 5 or 7?

Number of multiples of 5 between 1 and 100 = 20. Number of multiples of 7 between 1 and 100 = 14. Number of multiples of both 5 and 7 (35 and 70) = 2. Total favorable outcomes = 20 + 14 – 2 = 32. Probability = Number of favorable outcomes / Total tickets. = 32 / 100 = 0.32 or 32%.

Question 16: A box contains 5 red, 3 green, and 2 blue balls. Two balls are drawn at random. What is the probability that they are of different colors?

Total balls = 5 (red) + 3 (green) + 2 (blue) = 10. Probability of drawing one red and one green = (5/10) × (3/9) + (3/10) × (5/9). Probability of drawing one red and one blue = (5/10) × (2/9) + (2/10) × (5/9). Probability of drawing one green and one blue = (3/10) × (2/9) + (2/10) × (3/9). Total probability = Sum of the above probabilities.

Question 17: In a class of 60 students, 30 are boys. If two students are selected at random, what is the probability that both are girls?

Total girls = 60 – 30 = 30. Probability of first student being a girl = 30/60. After selecting one girl, remaining girls = 29, total students = 59. Probability of second student being a girl = 29/59. Total probability = (30/60) × (29/59).

Question 18: A fair die is rolled twice. What is the probability that the sum of the two rolls is 8?

The pairs that sum to 8 are: (2,6), (3,5), (4,4), (5,3), (6,2). Total outcomes when rolling twice = 6 × 6 = 36. Probability = Number of favorable outcomes / Total outcomes. = 5 / 36 ≈ 0.1389 or 13.89%.

Question 19: A bag contains 15 balls numbered 1 to 15. What is the probability of drawing a number that is either even or a multiple of 3?

Even numbers (2, 4, 6, 8, 10, 12, 14) = 7. Multiples of 3 (3, 6, 9, 12, 15) = 5. Common numbers in both sets (6, 12) = 2. Total favorable outcomes = 7 (even) + 5 (multiples of 3) – 2 (common) = 10. Probability = Number of favorable outcomes / Total balls. = 10 / 15 = 2 / 3 ≈ 0.6667 or 66.67%.

Question 20: A fair coin is tossed 5 times. What is the probability of getting exactly 3 heads?

The number of ways to get exactly 3 heads in 5 tosses can be calculated using the binomial formula: C(n, k) = n! / [k!(n-k)!], where C is the combination, n is the total number of events, and k is the number of successful events. C(5, 3) = 5! / [3!(5-3)!] = 10. Probability of getting a head in one toss = 1/2. Probability = 10 × (1/2) 3 × (1/2) 2 = 10/32 = 0.3125 or 31.25%.

Question 21: A deck of 52 cards is shuffled. What is the probability of drawing either a heart or a queen, but not the queen of hearts?

Total hearts = 13, including the queen of hearts. Total queens = 4, including the queen of hearts. Favorable outcomes = (13 hearts – 1 queen of hearts) + (4 queens – 1 queen of hearts) = 12 + 3 = 15. Probability = Number of favorable outcomes / Total outcomes = 15 / 52 ≈ 0.2885 or 28.85%.

Question 22: A bag contains 5 red, 6 blue, and 7 green balls. Three balls are drawn without replacement. What is the probability that they are drawn in the order red, blue, and green?

Probability of drawing a red ball first = 5/18. Then, probability of drawing a blue ball = 6/17 (after removing one red ball). Finally, probability of drawing a green ball = 7/16 (after removing one red and one blue ball). Total probability = (5/18) × (6/17) × (7/16) ≈ 0.0456 or 4.56%.

Question 23: In a lottery, there are 100 tickets numbered 1 to 100. What is the probability of drawing a number that is both a multiple of 5 and a multiple of 7?

Multiples of 5 and 7 between 1 and 100 are 35 and 70. Total favorable outcomes = 2. Probability = Number of favorable outcomes / Total tickets = 2 / 100 = 0.02 or 2%.

Question 24: A fair die is rolled three times. What is the probability of rolling a 6 each time?

The probability of rolling a 6 on one roll = 1/6. The probability of rolling three 6s in three rolls = (1/6) × (1/6) × (1/6) = 1/216 ≈ 0.00463 or 0.463%.

Question 25: A test consists of 10 true/false questions. To pass, a student must answer at least 8 questions correctly. If a student guesses on each question, what is the probability of passing the test?

The probability of guessing each question correctly = 1/2. The probability of getting exactly 8, 9, or 10 questions right can be calculated using the binomial probability formula: P(X=k) = C(n, k) × (p) k × (1-p) n-k , where C(n, k) is the combination. Calculate P(8) + P(9) + P(10) using the formula with n = 10, k = 8, 9, 10, and p = 1/2. Sum these probabilities to find the total probability of passing.

Through this article, we’ve explored various probability questions with solutions, offering you a good resource to practise and refine your skills. From basic probability concepts to more complex problems, these questions, based on the NCERT guidelines cater to learners at all levels.

FAQs on Probability

What is probability.

Probability measures the likelihood of an event occurring, ranging from 0 to 1.

What is a sample space?

The sample space is the set of all possible outcomes of an experiment.

How do you calculate the probability of an event?

P(E) = Number of favorable outcomes / Total number of outcomes.

What is the addition rule in probability?

For any events A and B, P(A ⋃ B) = P(A) + P(B) – P(A ⋂ B).

What is conditional probability?

Conditional probability is the probability of event B occurring given that event A has occurred, P(B | A) = P(A ⋂ B) / P(A).

Please Login to comment...

Similar reads.

• Math-Queries
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?