problem solving of polynomial function

Solving Polynomials

"Solving" means finding the "roots" ...

... a "root" (or "zero") is where the function is equal to zero :

In between the roots the function is either entirely above, or entirely below, the x-axis

Example: −2 and 2 are the roots of the function x 2 − 4

Let's check:

• when x = −2, then x 2 − 4 = (−2) 2 − 4 = 4 − 4 = 0
• when x = 2, then x 2 − 4 = 2 2 − 4 = 4 − 4 = 0

How do we solve polynomials? That depends on the Degree !

The first step in solving a polynomial is to find its degree.

The Degree of a Polynomial with one variable is ...

... the largest exponent of that variable.

When we know the degree we can also give the polynomial a name:

How To Solve

So now we know the degree, how to solve?

• Read how to solve Linear Polynomials (Degree 1) using simple algebra.
• Read how to solve Quadratic Polynomials (Degree 2) with a little work,
• It can be hard to solve Cubic (degree 3) and Quartic (degree 4) equations,
• And beyond that it can be impossible to solve polynomials directly.

So what do we do with ones we can't solve? Try to solve them a piece at a time!

If we find one root, we can then reduce the polynomial by one degree (example later) and this may be enough to solve the whole polynomial.

Here are some main ways to find roots.

1. Basic Algebra

We may be able to solve using basic algebra:

Example: 2x+1

2x+1 is a linear polynomial:

The graph of y = 2x+1 is a straight line

It is linear so there is one root.

Use Algebra to solve:

A "root" is when y is zero: 2x+1 = 0

Subtract 1 from both sides: 2x = −1

Divide both sides by 2: x = −1/2

And that is the solution:

(You can also see this on the graph)

We can also solve Quadratic Polynomials using basic algebra (read that page for an explanation).

2. By experience, or simply guesswork.

It is always a good idea to see if we can do simple factoring:

Example: x 3 +2x 2 −x

This is cubic ... but wait ... we can factor out "x":

x 3 +2x 2 −x = x(x 2 +2x−1)

Now we have one root (x=0) and what is left is quadratic, which we can solve exactly.

Example: x 3 −8

Again this is cubic ... but it is also the " difference of two cubes ":

x 3 −8 = x 3 −2 3

And so we can turn it into this:

x 3 −8 = (x−2)(x 2 +2x+4)

There is a root at x=2, because:

(2−2)(2 2 +2×2+4) = (0) (2 2 +2×2+4)

And we can then solve the quadratic x 2 +2x+4 and we are done

3. Graphically.

Graph the polynomial and see where it crosses the x-axis.

Graphing is a good way to find approximate answers, and we may also get lucky and discover an exact answer.

Caution: before you jump in and graph it, you should really know How Polynomials Behave , so you find all the possible answers!

This is useful to know: When a polynomial is factored like this:

f(x) = (x−a)(x−b)(x−c)...

Then a, b, c, etc are the roots !

So Linear Factors and Roots are related, know one and we can find the other.

(Read The Factor Theorem for more details.)

Example: f(x) = (x 3 +2x 2 )(x−3)

We see "(x−3)", and that means that 3 is a root (or "zero") of the function.

Well, let us put "3" in place of x:

f(x) = (3 3 +2·3 2 )(3−3)

f(3) = (3 3 +2·3 2 )( 0 )

Yes! f(3)=0, so 3 is a root.

How to Check

Found a root? Check it!

Simply put the root in place of "x": the polynomial should be equal to zero.

Example: 2x 3 −x 2 −7x+2

The polynomial is degree 3, and could be difficult to solve. So let us plot it first:

The curve crosses the x-axis at three points, and one of them might be at 2 . We can check easily, just put "2" in place of "x":

f(2) = 2(2) 3 −(2) 2 −7(2)+2 = 16−4−14+2 = 0

Yes! f(2)=0 , so we have found a root!

How about where it crosses near −1.8 :

f(−1.8) = 2(−1.8) 3 −(−1.8) 2 −7(−1.8)+2 = −11.664−3.24+12.6+2 = −0.304

No, it isn't equal to zero, so −1.8 will not be a root (but it may be close!)

But we did discover one root, and we can use that to simplify the polynomial, like this

Example (continued): 2x 3 −x 2 −7x+2

So, f(2)=0 is a root ... that means we also know a factor:

(x−2) must be a factor of 2x 3 −x 2 −7x+2

Next, divide 2x 3 −x 2 −7x+2 by (x−2) using Polynomial Long Division to find:

2x 3 −x 2 −7x+2 = (x−2)(2x 2 +3x−1)

So now we can solve 2x 2 +3x−1 as a Quadratic Equation and we will know all the roots.

That last example showed how useful it is to find just one root. Remember:

If we find one root, we can then reduce the polynomial by one degree and this may be enough to solve the whole polynomial.

How Far Left or Right

When trying to find roots, how far left and right of zero should we go?

There is a way to tell, and there are a few calculations to do, but it is all simple arithmetic. Read Bounds on Zeros for all the details.

Have We Got All The Roots?

There is an easy way to know how many roots there are. The Fundamental Theorem of Algebra says:

A polynomial of degree n ... ... has n roots (zeros) but we may need to use complex numbers

So: number of roots = the degree of polynomial .

Example: 2x 3 + 3x − 6

The degree is 3 (because the largest exponent is 3), and so:

There are 3 roots.

But Some Roots May Be Complex

Yes, indeed, some roots may be complex numbers (ie have an imaginary part), and so will not show up as a simple "crossing of the x-axis" on a graph.

But there is an interesting fact:

Complex Roots always come in pairs !

So we either get no complex roots, or 2 complex roots, or 4 , etc... Never an odd number.

Which means we automatically know this:

Positive or Negative Roots?

There is also a special way to tell how many of the roots are negative or positive called the Rule of Signs that you may like to read about.

Multiplicity of a Root

Sometimes a factor appears more than once. We call that Multiplicity :

• Multiplicity is how often a certain root is part of the factoring.

Example: f(x) = (x−5) 3 (x+7)(x−1) 2

This could be written out in a more lengthy way like this:

f(x) = (x−5)(x−5)(x−5)(x+7)(x−1)(x−1)

(x−5) is used 3 times, so the root "5" has a multiplicity of 3 , likewise (x+7) appears once and (x−1) appears twice. So:

• the root +5 has a multiplicity of 3
• the root −7 has a multiplicity of 1 (a "simple" root)
• the root +1 has a multiplicity of 2

Q: Why is this useful? A: It makes the graph behave in a special way!

When we see a factor like (x-r) n , "n" is the multiplicity, and

• even multiplicity just touches the axis at "r" (and otherwise stays one side of the x-axis)
• odd multiplicity crosses the axis at "r" (changes from one side of the x-axis to the other)

We can see it on this graph:

Example: f(x) = (x−2) 2 (x−4) 3

(x−2) has even multiplicity , so it just touches the axis at x=2

(x−4) has odd multiplicity , so it crosses the axis at x=4

• We can directly solve polynomials of Degree 1 (linear) and 2 (quadratic)
• For Degree 3 and up, graphs can be helpful
• Know how far left or right the roots may be
• Know how many roots (the same as its degree)
• Estimate how many may be complex, positive or negative

Free Mathematics Tutorials

Polynomial Questions and Problems with Solutions

Polynomial questions and problems related to graphs, x and y intercepts, coefficients, degree, leading coefficients, ... with detailed solutions are presented.

Popular Pages

• Polynomial Functions, Zeros, Factors and Intercepts
• Add and Subtract Polynomials - Grade 7 Math Questions and Problems With Answers
• Math Problems, Questions and Online Self Tests
• Factor Polynomials
• Free Algebra Questions and Problems with Answers

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• -4x^3+6x^2+2x=0
• 6+11x+6x^2+x^3=0
• 2x^5+x^4-2x-1=0
• 11+6x+x^2=-\frac{6}{x}
• How do you solve polynomials equations?
• To solve a polynomial equation write it in standard form (variables and canstants on one side and zero on the other side of the equation). Factor it and set each factor to zero. Solve each factor. The solutions are the solutions of the polynomial equation.
• What is polynomial equation?
• A polynomial equation is an equation formed with variables, exponents and coefficients. The highest exponent is the order of the equation.
• What is not polynomial?
• A non-polynomial function or expression is one that cannot be written as a polynomial. Non-polynomial functions include trigonometric functions, exponential functions, logarithmic functions, root functions, and more.
• Can 0 be a polynomial?
• Like any constant zero can be considered as a constant polynimial. It is called the zero polynomial and have no degree.

polynomial-equation-calculator

• High School Math Solutions – Exponential Equation Calculator Solving exponential equations is pretty straightforward; there are basically two techniques: <ul> If the exponents...

Please add a message.

Message received. Thanks for the feedback.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Polynomials

Solving Factoring Examples

The general technique for solving bigger-than-quadratic polynomials is pretty straightforward, but the process can be time-consuming.

Note: The terminology for this topic is often used carelessly. Technically, one "solves" an equation, such as "(polynomal) equals (zero)"; one "finds the roots" of a function, such as "( y ) equals (polynomial)". On this page, regardless of how the topic is framed, the point will be to find all of the solutions to "(polynomial) equals (zero)", even if the question is stated differently, such as "Find the roots of ( y ) equals (polynomial)".

Content Continues Below

MathHelp.com

The first step in finding the solutions of (that is, the x -intercepts of, plus any complex -valued roots of) a given polynomial function is to apply the Rational Roots Test to the polynomial's leading coefficient and constant term, in order to get a list of values that might possibly be solutions to the related polynomial equation. Your hand-in work is probably expected to contain this list, so write this out neatly.

Advertisement

You can follow this up with an application of Descartes' Rule of Signs , if you like, to narrow down which possible zeroes might be best to check. On the other hand, if you've got a graphing calculator you can use, it's easy to do a graph. The x - intercepts of the graph are the same as the (real-valued) zeroes of the equation. Seeing where the line looks as though it crosses the x -axis can quickly narrow down your list of possible zeroes that you'll want first to check.

Once you've found an x -value that you want to test, you then use synthetic division to see if you can get a zero remainder. If you do get a zero remainder, then you've not only found a zero of the original polynomial, but you've also reduced your polynomial by one degree, by effectively removing one factor.

Remember that synthetic division is, among other things, a form of polynomial division, so checking if x  =  a is a solution to "(polynomial) equals (zero)" is the same as dividing the linear factor x  −  a out of the related polynomial function "( y ) equals (polynomial)".

This also means that, after a successful division, you've also successfully taken a factor out. You should not then return to the original polynomial for your next computation for finding the other zeroes. You should instead work with the output of the synthetic division. It's smaller, so it's easier to work with.

(This method will be demonstrated in the examples below.)

You should not be surprised to see some complicated solutions to your polynomials (that is, solutions containing square roots or complex numbers, or both); these zeroes will come from applying the Quadratic Formula to (what is usually) the final (quadratic) factor of your polynomial. You should expect that the answers will be messy.

Here's how the process plays out in practice:

Find all the zeroes of: y = 2 x 5 + 3 x 4 − 30 x 3 − 57 x 2 − 2 x + 24

First, I'll apply the Rational Roots Test—

Wait. Actually, the first thing I'll do is apply a trick I've learned. First, I'll check to see if either x  = 1 or x  = −1 is a root.

(These are the simplest roots to test for. This isn't an "official" first step, but it can often be a timesaver, because (a) it's amazing how often one of these is a zero, and (b) you can just look at the powers and the numbers to figure out if either works, because of how 1 and −1 simplify.)

When x  = 1 , the polynomial evaluates as:

2 + 3 − 30 − 57 − 2 + 24 = −60

This isn't equal to zero, so x  = 1 isn't a root. But when x  = −1 , I get:

−2 + 3 + 30 − 57 + 2 + 24 = 0

This time, it did equal zero, so now I know that x  = −1 is a root, and I can take "prove" this (in my hand-in work) by using synthetic division:

The last line of this division shows me with the new, smaller polynomial equation I'm working with now:

2 x 4 + x 3 − 31 x 2 − 26 x + 24 = 0

(I'd started with a degree-five polynomial. Since I've effectively divided out the factor x  + 1 , I've reduced the degree of the polynomial by 1 . That's how I know the last line of the division represents a degree-four polynomial.)

I've taken care of checking the two easiest zeroes. Now I'll apply the Rational Roots Test to what's left in order to get a list of potential zeroes to try:

From experience (mostly by having worked extra homework problems), I've learned that most of these exercises have their zeroes somewhere near the middle of the list, rather than at the extremes. This isn't always true, of course, but it's usually better to stay away from the larger numbers, at least when I'm getting started.

So, in this case, I won't start off by trying stuff like x  = −24 or x  = 12 . Instead, I'll start out with smaller values like x  = 2 .

And I can narrow down my options further by "cheating" and looking at the graph:

This is a fourth-degree polynomial, so it has, at most, four x -intercepts, and I can see all four of them on the graph. This means that I won't have any complex-valued zeroes.

It also looks like there may be zeroes near −1.5 and 0.5 . But the clearest solution looks to be at x  = 4 and since whole numbers are easier to work with than fractions, x  = 4 would probably be a good next value to try:

The zero remainder (at the far right of the bottom row) tells me that x  = 4 is indeed a root. And the bottom row of the synthetic division tells me that I'm now left with solving the following:

2 x 3 + 9 x 2 + 5 x − 6 = 0

Looking at the constant term " 6 " in the polynomial above, and with the Rational Roots Test in mind, I can see that the following values:

x = ±24, ±12, ±8, −4

...from my original application of the Rational Roots Test won't work for the current polynomial. Even if I didn't already know this from having checked the graph, I can see that they won't fit with the new polynomial's leading coefficient and constant term. So I can cross these values off of my list now.

(Always check the list of possible zeroes as you go. The Rational Roots Test will sometimes give a very long list of possibilities, and it can be helpful to notice that some of those values can be ignored, especially if you don't have a graphing calculator to "cheat" with.)

2 x 2 + 6 x − 4 = 0

Dividing through by 2 to get smaller numbers gives me:

x 2 + 3 x − 2 = 0

I can apply the Quadratic Formula to this:

This gives me the remaining two roots of the original polynomial function. (I plugged the exact values into my calculator, to confirm that they match up with what I'd already seen on the graph, so I'd be certain that my answer was correct. I won't hand in these approximations, though.)

My complete answer is:

Asking you to find the zeroes of a polynomial function, y equals (polynomial), means the same thing as asking you to find the solutions to a polynomial equation, (polynomial) equals (zero). The zeroes of a polynomial are the values of x that make the polynomial equal to zero. Either task may be referred to as "solving the polynomial".

So the above problem could have been stated along the lines of:

Find the solutions to 2 x 5 + 3 x 4 − 30 x 3 − 57 x 2 − 2 x + 24 = 0

Find the solutions to 2 x 5 + 3 x 4 − 30 x 3 − 57 x 2 − 2 x = −24

...and the answers would have been the exact same list of x -values.

URL: https://www.purplemath.com/modules/solvpoly.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

How to Solve Polynomial Equations

Copyright © 2002–2024 by Stan Brown, BrownMath.com

Summary: In algebra you spend lots of time solving polynomial equations or factoring polynomials (which is the same thing). It would be easy to get lost in all the techniques, but this paper ties them all together in a coherent whole.

Factor = Root

Exact or approximate, step by step, cubic and quartic formulas, step 1. standard form and simplify, descartes’ rule of signs, complex roots, irrational roots, multiple roots, step 3. quadratic factors, monomial factors, special products, rational roots, graphical clues, boundaries on roots, step 5. divide by your factor, web calculators, ti calculators, complete example, what’s new, the master plan.

Make sure you aren’t confused by the terminology. All of these are the same:

• Solving a polynomial equation p ( x ) = 0
• Finding roots of a polynomial equation p ( x ) = 0
• Finding zeroes of a polynomial function p ( x )
• Factoring a polynomial function p ( x )

There’s a factor for every root, and vice versa. ( x − r ) is a factor if and only if r is a root. This is the Factor Theorem : finding the roots or finding the factors is essentially the same thing. (The main difference is how you treat a constant factor .)

Most often when we talk about solving an equation or factoring a polynomial, we mean an exact (or analytic) solution . The other type, approximate (or numeric) solution , is always possible and sometimes is the only possibility.

When you can find it, an exact solution is usually better . You can always find a numerical approximation to an exact solution, but going the other way is much more difficult. This page spends most of its time on methods for exact solutions, but also tells you what to do when analytic methods fail — or when you actually want an approximate solution, as in many engineering and science problems .

How do you find the factors or zeroes of a polynomial (or the roots of a polynomial equation)? Basically, you whittle . Every time you chip a factor or root off the polynomial, you’re left with a polynomial that is one degree simpler. Use that new reduced polynomial to find the remaining factors or roots.

Follow this procedure step by step:

If you’re down to a cubic or quartic equation (degree 3 or 4), you have a choice of continuing with factoring (step 4) or using the cubic or quartic formulas . These formulas are a lot of work, so most people prefer to keep factoring.

• Find one rational factor or root. This is the hard part, but there are lots of techniques to help you.   [  details  ] If you can find a factor or root, continue with step 5 below; if you can’t (or if you actually want an approximate solution) , go to step 6.
• Divide by your factor . This leaves you with a new reduced polynomial whose degree is 1 less.   [  details  ]   For the rest of the problem, you’ll work with the reduced polynomial and not the original. Continue at step 3.
• If you can’t find a factor or root , turn to numerical methods.   [  details  ] Then go to step 7.
• If this was an equation to solve, write down the roots . If it was a polynomial to factor, write it in factored form , including any constant factors you took out in step 1.

This is an example of an algorithm , a set of steps that will lead to a desired result in a finite number of operations. It’s an iterative strategy, because the middle steps are repeated as long as necessary.

The methods given here—find a rational root and use synthetic division—are the easiest. But if you can’t find a rational root, there are special methods for cubic equations (degree 3) and quartic equations (degree 4), both at Mathworld. An alternative approach is provided by Dick Nickalls in PDF for cubic and quartic equations.

This is an easy step—easy to overlook, unfortunately. If you have a polynomial equation , put all terms on one side and 0 on the other. And whether it’s a factoring problem or an equation to solve, put your polynomial in standard form, from highest to lowest power .

For instance, you cannot solve this equation in this form:

x ³ + 6 x ² + 12 x = −8

You must change it to this form:

x ³ + 6 x ² + 12 x + 8 = 0

Also make sure you have simplified, by factoring out any common factors . This may include factoring out a −1 so that the highest power has a positive coefficient. Example: to factor

7 − 6 x − 15 x ² − 2 x ³

begin by putting it in standard form:

−2 x ³ − 15 x ² − 6 x + 7

and then factor out the −1

−(2 x ³ + 15 x ² + 6 x − 7) or (−1)(2 x ³ + 15 x ² + 6 x − 7)

If you’re solving an equation, you can throw away any common constant factor. (Technically, you’re dividing left and right sides by that constant factor.) But if you’re factoring a polynomial, you must keep the common factor .

Example: To solve 8 x ² + 16 x  + 8 = 0, you can divide left and right by the common factor 8. The equation x ² + 2 x  + 1 = 0 has the same roots as the original equation .

But to factor 8 x ² + 16 x  + 8 , you recognize the common factor of 8 and rewrite the polynomial as 8( x ² + 2 x  + 1), which is identical to the original polynomial . (While you will focus your further factoring efforts on x ² + 2 x  + 1, it would be an error to write that the original polynomial equals x ² + 2 x  + 1.)

Your “common factor” may be a fraction, because you must factor out any fractions so that the polynomial has integer coefficients .

Example: To solve (1/3) x ³ + (3/4) x ² − (1/2) x  + 5/6 = 0, you recognize the common factor of 1/12 and divide both sides by 1/12. This is exactly the same as recognizing and multiplying by the lowest common denominator of 12. Either way, you get 4 x ³ + 9 x ² − 6 x  + 10 = 0, which has the same roots as the original equation .

Step 2. How Many Roots?

A polynomial of degree n will have n roots, some of which may be multiple roots .

How do you know this is true? The Fundamental Theorem of Algebra tells you that the polynomial has at least one root. The Factor Theorem tells you that if r is a root then ( x − r ) is a factor. But if you divide a polynomial of degree n by a factor ( x − r ), whose degree is 1, you get a polynomial of degree n −1. Repeatedly applying the Fundamental Theorem and Factor Theorem gives you n roots and n factors (not necessarily all different) .

Descartes’ Rule of Signs can tell you how many positive and how many negative real zeroes the polynomial has. This is a big labor-saving device, especially when you’re deciding which possible rational roots to pursue.

p ( x ) = x 5 − 2 x 3 + 2 x 2 − 3 x + 12

has four variations in sign.

Descartes’ Rule of Signs:

Example: Consider p ( x ) above. Since it has four variations in sign, there must be either four positive roots, two positive roots, or no positive roots.

p (− x ) = (− x ) 5  − 2(− x ) 3  + 2(− x ) 2  − 3(− x ) + 12

p (− x ) = − x 5  + 2 x 3  + 2 x 2  + 3 x  + 12

p (− x ) has one variation in sign, and therefore the original p ( x ) has one negative root. Since you know that p ( x ) must have a negative root, but it may or may not have any positive roots, you would look first for negative roots.

p ( x ) is a fifth-degree polynomial, and therefore it must have five zeros. Since x is not a factor, you know that x  = 0 is not a zero of the polynomial. (For a polynomial with real coefficients, like this one, complex roots occur in pairs .) Therefore there are three possibilities:

If a polynomial has real coefficients , then either all roots are real or there are an even number of non-real complex roots, in conjugate pairs .

For example, if 5+2i is a zero of a polynomial with real coefficients, then 5−2i must also be a zero of that polynomial. It is equally true that if ( x −5−2i) is a factor then ( x −5+2i) is also a factor.

Why is this true? Because when you have a factor with an imaginary part and multiply it by its complex conjugate you get a real result:

( x −5−2i)( x −5+2i) = x ²−10 x +25−4i² = x ²−10 x +29

If ( x −5−2i) was a factor but ( x −5+2i) was not, then the polynomial would end up with imaginaries in its coefficients, no matter what the other factors might be. If the polynomial has only real coefficients, then any complex roots must occur in conjugate pairs.

For similar reasons, if the polynomial has rational coefficients then the irrational roots involving square roots occur (if at all) in conjugate pairs. If ( x −2+√3) is a factor of a polynomial with rational coefficients, then ( x −2−√3) must also be a factor. To see why, remember how you rationalize a binomial denominator; or just check what happens when you multiply those two factors.

As Jeff Beckman pointed out (20 June 2006), this is emphatically not true for odd roots. For instance, x ³−2 = 0 has three roots: 3 √ 2 and two complex roots.

It’s an interesting problem whether irrationals involving even roots of order ≥4 must also occur in conjugate pairs. I don’t have an immediate answer.

When a given factor ( x − r ) occurs m times in a polynomial, r is called a multiple root or a root of multiplicity m .

Examples: Compare these two polynomials and their graphs:

f ( x ) =  ( x −1)( x −4) 2  = x 3  − 9 x 2  + 24 x  − 16

g ( x ) = ( x −1) 3 ( x −4) 2  = x 5 − 11 x 4 + 43 x 3 − 73 x 2 + 56 x − 16

These polynomials have the same zeroes, but the root 1 occurs with different multiplicities. Look at the graphs:

Both polynomials have zeroes at 1 and 4 only. f ( x ) has degree 3, which means three roots. You see from the factors that 1 is a root of multiplicity 1 and 4 is a root of multiplicity 2. Therefore the graph crosses the axis at x  = 1 (but is not horizontal there) and touches at x  = 4 without crossing.

By contrast, g ( x ) has degree 5. ( g ( x ) = f ( x ) times ( x −1) 2 .) Of the five roots, 1 occurs with multiplicity 3: the graph crosses the axis at x  = 1 and is horizontal there; 4 occurs with multiplicity 2, and the graph touches the axis at x  = 4 without crossing.

When you have quadratic factors (Ax²+Bx+C), it may or may not be possible to factor them further.

For example, suppose you have a factor of 12 x ²− x −35. Can that be factored further? By trial and error you’d have to try a lot of combinations! Instead, use the fact that factors correspond to roots , and apply the formula to find the roots of 12 x ²− x −35 = 0, like this:

x = [ −(−1) ± √ 1 − 4(12)(−35) ] / 2(12)

x = [ 1 ± √ 1681 ] / 24

√ 1681 = 41, and therefore

x = [ 1 ± 41 ] / 24

x = 42/24 or −40/24

x = 7/4 or −5/3

If 7/4 and −5/3 are roots, then ( x −7/4) and ( x +5/3) are factors. Therefore

12 x ²− x −35 = 12( x −7/4)( x +5/3) or (4 x −7)(3 x +5)

What about x ²−5 x +7? This one looks like it’s prime, but how can you be sure? Again, apply the formula:

x = [ −(−5) ± √ 25 − 4(1)(7) ] / 2(1)

x = [ 5 ± √ −3 ] / 2

What you do with that depends on the original problem. If it was to factor over the reals, then x ²−5 x +7 is prime. But if that factor was part of an equation and you were supposed to find all complex roots, you have two of them:

x = 5/2 + (√ 3 /2)i, x = 5/2 − (√ 3 /2)i

Since the original equation had real coefficients, these complex roots occur in a conjugate pair .

Step 4. Find One Factor or Root

This step is the heart of factoring a polynomial or solving a polynomial equation. There are a lot of techniques that can help you to find a factor.

Sometimes you can find factors by inspection (see the first two sections that follow). This provides a great shortcut, so check for easy factors before starting more strenuous methods .

f ( x ) = 4 x 6  + 12 x 5  + 12 x 4  + 4 x 3

you should immediately factor it as

f ( x ) = 4 x 3 ( x 3  + 3 x 2  + 3 x  + 1)

Getting the 4 out of there simplifies the remaining numbers, the x 3 gives you a root of x  = 0 (with multiplicity 3), and now you have only a cubic polynomial (degree 3) instead of a sextic (degree 6). In fact, you should now recognize that cubic as a special product , the perfect cube ( x +1) 3 .

When you factor out a common variable factor, be sure you remember it at the end when you’re listing the factor or roots. x ³+3 x ²+3 x +1 = 0 has certain roots, but x ³( x ³+3 x ²+3 x +1) = 0 has those same roots and also a root at x  = 0 (with multiplicity 3) .

Be alert for applications of the Special Products . If you can apply them, your task becomes much easier. The Special Products are

• perfect square (2 forms): A ² ± 2 A B + B ² = ( A ± B )²
• sum of squares: A ² + B ² cannot be factored on the reals, in general (for exceptional cases see How to Factor the Sum of Squares )
• difference of squares: A ² − B ² = ( A + B )( A − B )
• perfect cube (2 forms): A ³ ± 3 A ² B + 3 A B ² ± B ³ = ( A ± B )³
• sum of cubes: A ³ + B ³ = ( A + B )( A ² − A B + B ²)
• difference of cubes: A ³ − B ³ = ( A − B )( A ² + A B + B ²)

The expressions for the sum or difference of two cubes look as though they ought to factor further, but they don’t. A ²± A B + B ² is prime over the reals.

p ( x ) = 27 x ³ − 64

You should recognize this as

p ( x ) = (3 x )³ − 4³

You know how to factor the difference of two cubes:

p ( x ) = (3 x −4)(9 x ²+12 x +16)

Bingo! As soon as you get down to a quadratic, you can apply the Quadratic Formula and you’re done.

Here’s another example:

q ( x ) = x 6  + 16 x 3  + 64

This is just a perfect square trinomial, but in x 3 instead of x . You factor it exactly the same way:

q ( x ) = ( x 3 ) 2 + 2(8)( x 3 ) + 8 2

q ( x ) = ( x 3  + 8) 2

And you can easily factor ( x 3 +8) 2 as ( x +2) 2 ( x 2 −2 x +4) 2 .

Assuming you’ve already factored out the easy monomial factors and special products , what do you do if you’ve still got a polynomial of degree 3 or higher?

The answer is the Rational Root Test . It can show you some candidate roots when you don’t see how to factor the polynomial, as follows.

f ( x ) = a n x n + … + a o

The Rational Root Theorem tells you that if the polynomial has a rational zero then it must be a fraction p / q , where p is a factor of the trailing constant a o and q is a factor of the leading coefficient a n .

f ( x ) = 2 x 4 − 11 x 3 − 6 x 2 + 64 x + 32

The factors of the leading coefficient (2) are 2 and 1. The factors of the constant term (32) are 1, 2, 4, 8, 16, and 32. Therefore the possible rational zeroes are ±1, 2, 4, 8, 16, or 32 divided by 2 or 1:

± any of 1/2, 1/1, 2/2, 2/1, 4/2, 4/1, 8/2, 8/1, 16/2, 16/1, 32/2, 32/1

reduced: ± any of ½, 1, 2, 4, 8, 16, 32

What do we mean by saying this is a list of all the possible rational roots ? We mean that no other rational number, like ¼ or 32/7, can be a zero of this particular polynomial.

Caution : Don’t make the Rational Root Test out to be more than it is. It doesn’t say those rational numbers are roots, just that no other rational numbers can be roots. And it doesn’t tell you anything about whether some irrational or even complex roots exist. The Rational Root Test is only a starting point.

Suppose you have a polynomial with non-integer coefficients. Are you stuck? No, you can factor out the least common denominator (LCD) and get a polynomial with integer coefficients that way. Example:

(1/2) x ³ − (3/2) x ² + (2/3) x − 1/2

The LCD is 1/6. Factoring out 1/6 gives the polynomial

(1/6)(3 x ³ − 9 x ² + 4 x − 3)

The two forms are equivalent, and therefore they have the same roots. But you can’t apply the Rational Root Test to the first form, only to the second. The test tells you that the only possible rational roots are ± any of 1/3, 1, 3.

Once you’ve identified the possible rational zeroes, how can you screen them? The brute-force method would be to take each possible value and substitute it for x in the polynomial: if the result is zero then that number is a root. But there’s a better way.

Use synthetic division to see if each candidate makes the polynomial equal zero. This is better for three reasons. First, it’s computationally easier, because you don’t have to compute higher powers of numbers. Second, at the same time it tells you whether a given number is a root, it produces the reduced polynomial that you’ll use to find the remaining roots. Finally, the results of synthetic division may give you an upper or lower bound even if the number you’re testing turns out not to be a root.

Sometimes Descartes’ Rule of Signs can help you screen the possible rational roots further. For example, the Rational Root Test tells you that if

g ( x ) = 2 x 4 + 13 x 3 + 20 x 2 + 28 x + 8

has any rational roots, they must come from the list ± any of ½, 1, 2, 4, 8. But don’t just start off substituting or synthetic dividing. Since there are no sign changes, there are no positive roots. Are there any negative roots?

g (− x ) = 2 x 4 − 13 x 3 + 20 x 2 − 28 x + 8

has four sign changes. Therefore there could be as many as four negative roots. (There could also be two negative roots, or none.) There’s no guarantee that any of the roots are rational, but any root that is rational must come from the list −½, −1, −2, −4, −8.

(If you have a graphing calculator, you can pre-screen the rational roots by graphing the polynomial and seeing where it seems to cross the x  axis. But you still need to verify the root algebraically, to see that g ( x ) is exactly 0 there, not just nearly 0.)

Remember, the Rational Root Test guarantees to find all rational roots. But it will completely miss real roots that are not rational, like the roots of x ² − 2 = 0, which are ±√2, or the roots of x ² + 4 = 0, which are ±2i.

p ( x ) = 2 x 4 − 11 x 3 − 6 x 2 + 64 x + 32

The Rational Root Theorem tells you that the only possible rational zeroes are ±½, 1, 2, 4, 8, 16, 32. But suppose you factor out the 2 (as I once did in class), writing the equivalent function

p ( x ) = 2( x 4 − (11/2) x 3 − 3 x 2 + 32 x + 16)

This function is the same as the earlier one, but you can no longer apply the Rational Root Test because the coefficients are not integers. In fact −½ is a zero of p ( x ), but it did not show up when I (illegally) applied the Rational Root Test to the second form. My mistake was forgetting that the Rational Root Theorem applies only when all coefficients of the polynomial are integers.

By graphing the function—either by hand or with a graphing calculator—you can get a sense of where the roots are, approximately, and how many real roots exist.

Example: If the Rational Root Test tells you that ±2 are possible rational roots, you can look at the graph to see if it crosses or touches the x  axis at 2 or −2. If so, use synthetic division to verify that the suspected root actually is a root. Yes, you always need to check—from the graph you can never be sure whether the intercept is at your possible rational root or just near it.

Some techniques don’t tell you the specific value of a root, but rather that a root exists between two values or that all roots are less than a certain number of greater than a certain number. This helps narrow down your search.

Intermediate Value Theorem

This theorem tells you that if the graph of a polynomial is above the x  axis for one value of x and below the x  axis for another value of x , it must cross the x  axis somewhere between. (If you can graph the function , the crossings will usually be obvious.)

p ( x ) = 3 x ³ + 4 x ² − 20 x −32

The rational roots (if any) must come from the list ± any of 1/3, 2/3, 1, 4/3, 2, 8/3, 4, 16/3, 8, 32/3, 16, 32. Naturally you’ll look at the integers first, because the arithmetic is easier. Trying synthetic division , you find p (1) = −45, p (2) = −22, and p (4) = 144. Since p (2) and p (4) have opposite signs, you know that the graph crosses the axis between x  = 2 and x  = 4, so there is at least one root between those numbers. In other words, either 8/3 is a root, or the root(s) between 2 and 4 are irrational. (In fact, synthetic division reveals that 8/3 is a root.)

The Intermediate Value Theorem can tell you where there is a root, but it can’t tell you where there is no root. For example, consider

q ( x ) = 4 x ² − 16 x + 15

q (1) and q (3) are both positive, but that doesn’t tell you whether the graph might touch or cross the axis between. (It actually crosses the axis twice, at x  = 3/2 and x  = 5/2.)

Upper and Lower Bounds

One side effect of synthetic division is that even if the number you’re testing turns out not to be a root, it may tell you that all the roots are smaller or larger than that number:

• If you do synthetic division by a positive number a , and every number in the bottom row is positive or zero, then a is an upper bound for the roots, meaning that all the real roots are ≤  a .

What if the bottom row contains zeroes? A more complete statement is that alternating nonnegative and nonpositive signs , after synthetic division by a negative number, show a lower bound on the root. The next two examples clarify that.

(By the way, the rule for lower bounds follows from the rule for upper bounds. Lower limits on roots of p ( x ) equal upper limits on roots of p (− x ), and dividing by (− x + r ) is the same as dividing by −( x − r ).)

q ( x ) = x 3  + 2 x 2  − 3 x  − 4

Using the Rational Root Test , you identify the only possible rational roots as ±4, ±2, and ±1. You decide to try −2 as a possible root, and you test it with synthetic division:

−2 is not a root of the equation f ( x ) = 0. The third row shows alternating signs, and you were dividing by a negative number; however, that zero mucks things up. Recall that you have a lower bound only if the signs in the bottom row alternate nonpositive and nonnegative. The 1 is positive (nonnegative), and the 0 can count as nonpositive, but the −3 doesn’t qualify as nonnegative. The alternation is broken, and you do not know whether there are roots smaller than −2. (In fact, graphical or numerical methods would show a root around −2.5.) Therefore you need to try the lower possible rational root, −4:

Here the signs do alternate; therefore you know there are no roots below −4. (The remainder −24 shows you that −4 itself isn’t a root.)

r ( x ) = x ³ + 3 x ² − 3

The Rational Root Test tells you that the possible rational roots are ±1 and ±3. With synthetic division for −3:

−3 is not a root, but the signs do alternate here, since the first 0 counts as nonpositive and the second as nonnegative. Therefore −3 is a lower bound to the roots, meaning that the equation has no real roots lower than −3.

Coefficients and Roots

There is an interesting relationship between the coefficients of a polynomial and its zeroes. I mention it last because it is more suited to forming a polynomial that has zeroes with desired properties, rather than finding zeroes of an existing polynomial. However, if you know all the roots of a polynomial but one or two, you can easily use this technique to find the remaining root.

Consider the polynomial

f ( x ) = a n x n + a n −1 x n −1 + a n −2 x n −2 + … + a 2 x 2 + a 1 x + a o

The following relationships exist:

Example: f ( x ) = x 3  − 6 x 2  − 7 x  − 8 has degree 3, and therefore at most three real zeroes. If we write the real zeroes as r 1 , r 2 , r 3 , then the sum of the roots is r 1  + r 2  + r 3  = −(−6) = 6; the sum of the products of roots taken two at a time is r 1 r 2  + r 1 r 3  + r 2 r 3  = −7, and the product of the roots is r 1 r 2 r 3  = (−1) 3 (−8) = 8.

Example: Given that the polynomial

g ( x ) = x 5 − 11 x 4 + 43 x 3 − 73 x 2 + 56 x − 16

has a triple root at x  = 1, find the other two roots.

Solution: Let the other two roots be c and d . Then you know that the sum of the all roots is 1 + 1 + 1 + c  + d  = −(−11) = 11, or c  + d  = 8. You also know that the product of all the roots is 1 × 1 × 1 × c d  = (−1) 5 (−16) = 16, or c d  = 16. c  + d  = 8, c d  = 16; therefore c  = d  = 4, so the remaining roots are a double root at x  = 4.

More Coefficients and Roots

There are several further theorems about the relationship between coefficients and roots. Wikipedia’s article Properties of Polynomial Roots gives a good though somewhat terse summary.

Remember that r is a root if and only if x − r is a factor; this is the Factor Theorem . So if you want to check whether r is a root, you can divide the polynomial by x − r and see whether it comes out even (remainder of 0). Elizabeth Stapel has a nice example of dividing polynomials by long division.

But it’s easier and faster to do synthetic division. If your synthetic division is a little rusty, you might want to look at Dr. Math’s short Synthetic Division tutorial ; if you need a longer tutorial, Elizabeth Stapel’s Synthetic Division is excellent. (Dr. Math also has a page on why Synthetic Division works .)

Synthetic division also has some side benefits. If your suspected root actually is a root, synthetic division gives you the reduced polynomial . And sometimes you also luck out and synthetic division shows you an upper or lower bound on the roots.

You can use synthetic division when you’re dividing by a binomial of the form x − r for a constant r . If you’re dividing by x −3, you’re testing whether 3 is a root and you synthetic divide by 3 (not −3). If you’re dividing by x +11, you’re testing whether −11 is a root and you synthetic divide by −11 (not 11).

p ( x ) = 4 x 4  − 35 x 2  − 9

You suspect that x −3 might be a factor, and you test it by synthetic division, like this:

Since the remainder is 0, you know that 3 is a root of p ( x ) = 0, and x −3 is a factor of p ( x ). But you know more. Since 3 is positive and the bottom row of the synthetic division is all positive or zero, you know that all the roots of p ( x ) = 0 must be ≤ 3. And you also know that

p ( x ) = ( x −3)(4 x 3  + 12 x 2  +  x  + 3)

4 x 3  + 12 x 2  +  x  + 3 is the reduced polynomial . All of its factors are also factors of the original p ( x ), but its degree is one lower , so it’s easier to work with.

Step 6. Numerical Methods

When your equation has no more rational roots (or your polynomial has no more rational factors), you can turn to numerical methods to find the approximate value of irrational roots:

• Newton’s method converges quickly, but the derivative must exist and be continuous, and of course you need to know how to find the derivative. Wikipedia has a decent article on the method, and my article Newton’s Method on TI-83/84 or TI-89 walks you through the calculator procedure.
• The Regula falsi method can be slower than Newton’s method, but it doesn’t have the limitations of Newton’s method.

A search like this one will find a bazillion online polynomial calculators. However, many of them fail in one way or another on the example below : they miss the complex roots, or they can’t show the steps in the calculation, or ask for money to show the steps.

MathPortal’s Polynomial Equation Solver is an excellent free resource, and it did a fine job with that example .

If you have a TI-83 or TI-84 , you can get the zeroes of a polynomial numerically. Graph the polyomial, then use calc  » zero to find the real zeroes. This YouTube video shows you the process. (This won’t help you with the complex ones, if any.)

Recent versions of the TI-84 , beginning with the TI-84 Silver Edition, have APPS  » PlySmlt2  » POLYNOMIAL ROOT FINDER , which includes an option to show complex roots. This YouTube video shows the process and gives some tips for the black&white calculator, and this one does the same for the color TI-84s.

The TI-89 will give you exact solutions, if possible, for real and complex roots. (You may need to press the MODE key, scroll down to Exact/Approx , and change it to Exact.)

Select F2:Algebra  » A:Complex  » cSolve , then enter your equation including = 0, press the comma key, and then the name of your variable, and finally press ) and ENTER. For the example below , the input line should look like this:

cSolve(4x³+15x−36=0,x)

This video shows how to get exact solutions or numeric solutions on the TI-89.

Solve for all complex roots:

4 x ³ + 15 x − 36 = 0

(We’ll call the left-hand side f ( x ).)

Step 1.   The equation is already in standard form, with only zero on one side, and powers of x from highest to lowest. There are no common factors.

Step 2.   Since the equation has degree 3, there will be 3 roots. There is one variation in sign, and from Descartes’ Rule of Signs you know there must be one positive root. Examine the polynomial with − x replacing x :

f (− x ) = −4 x ³ − 15 x − 36

There are no variations in sign, which means there are no negative roots. The other two roots must therefore be complex, and conjugates of each other.

Steps 3 and 4.   The possible rational roots are unfortunately rather numerous: any of 1, 2, 3, 4, 6, 9, 12, 18, 36 divided by any of 4, 2, 1. (Only positive roots are listed because you have already determined that there are no negative roots for this equation.) You decide to try 1 first:

1 is not a root, so you test 2:

Alas, 2 is not a root either. But notice that f (1) = −17 and f (2) = 26. They have opposite signs, which means that the graph crosses the x  axis between x  = 1 and x  = 2, and a root is between 1 and 2. (In this case it’s the only root, since you have determined that there is one positive root and there are no negative roots.)

The only possible rational root between 1 and 2 is 3/2, and therefore either 3/2 is a root or the root is irrational. You try 3/2 by synthetic division:

Hooray! 3/2 is a root. The reduced polynomial is 4 x ² + 6 x  + 24. In other words,

(4 x ³ + 15 x  − 36) ÷ ( x −3/2) = 4 x ² + 6 x  + 24

The reduced polynomial has degree 2, so there is no need for more trial and error, and you continue to step 5.

Step 5.   Now you must solve

4 x ² + 6 x  + 24 = 0

First divide out the common factor of 2:

2 x ² + 3 x  + 12 = 0

It’s no use trying to factor that quadratic, because you determined using Descartes’ Rule of Signs that there are no more real roots. So you use the quadratic formula :

x = [ −3 ± √ 9 − 4(2)(12) ] / 2(2)

x = [ −3 ± √ −87 ] / 4

x = −3/4 ± (√ 87 /4)i

Step 6.   Remember that you found a root in an earlier step! The full list of roots is

3/2,  −3/4 + (√ 87 /4)i,  −3/4 − (√ 87 /4)i

• 26 Mar 2022 : Rewrote step 6 to recommend Newton’s method and the Regula Falsi method specifically, and added a Web calculator and TI calculator methods . Added “usually” to the statement that exact solutions are better, and suggested that numeric solutions may be appropriate for engineering and science Made a number of text changes for clarity.
• 14/15 Nov 2021 : Updated links here and here . Updated all http: links to https:.
• (intervening changes suppressed)
• 15 Feb 2002 : First publication.

Updates and new info: https://BrownMath.com/alge/

Site Map | Searches | Home Page | Contact

Zeros of Polynomial Functions

Solve real-world applications of polynomial equations.

We have now introduced a variety of tools for solving polynomial equations. Let’s use these tools to solve the bakery problem from the beginning of the section.

Example 8: Solving Polynomial Equations

A new bakery offers decorated sheet cakes for children’s birthday parties and other special occasions. The bakery wants the volume of a small cake to be 351 cubic inches. The cake is in the shape of a rectangular solid. They want the length of the cake to be four inches longer than the width of the cake and the height of the cake to be one-third of the width. What should the dimensions of the cake pan be?

Begin by writing an equation for the volume of the cake. The volume of a rectangular solid is given by [latex]V=lwh[/latex]. We were given that the length must be four inches longer than the width, so we can express the length of the cake as [latex]l=w+4[/latex]. We were given that the height of the cake is one-third of the width, so we can express the height of the cake as [latex]h=\frac{1}{3}w[/latex]. Let’s write the volume of the cake in terms of width of the cake.

Substitute the given volume into this equation.

Descartes’ rule of signs tells us there is one positive solution. The Rational Zero Theorem tells us that the possible rational zeros are [latex]\pm 3,\pm 9,\pm 13,\pm 27,\pm 39,\pm 81,\pm 117,\pm 351[/latex], and [latex]\pm 1053[/latex]. We can use synthetic division to test these possible zeros. Only positive numbers make sense as dimensions for a cake, so we need not test any negative values. Let’s begin by testing values that make the most sense as dimensions for a small sheet cake. Use synthetic division to check [latex]x=1[/latex].

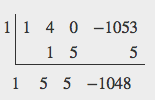
Since 1 is not a solution, we will check [latex]x=3[/latex].

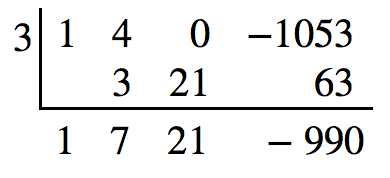
Since 3 is not a solution either, we will test [latex]x=9[/latex].

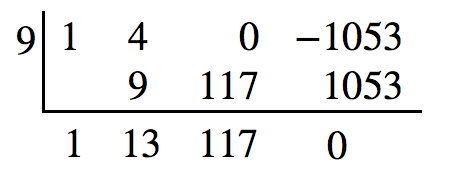
Synthetic division gives a remainder of 0, so 9 is a solution to the equation. We can use the relationships between the width and the other dimensions to determine the length and height of the sheet cake pan.

The sheet cake pan should have dimensions 13 inches by 9 inches by 3 inches.

A shipping container in the shape of a rectangular solid must have a volume of 84 cubic meters. The client tells the manufacturer that, because of the contents, the length of the container must be one meter longer than the width, and the height must be one meter greater than twice the width. What should the dimensions of the container be?

3 meters by 4 meters by 7 meters

• Precalculus. Authored by : Jay Abramson, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download For Free at : http://cnx.org/contents/[email protected].

Multiplying Polynomials Word Problems - Examples & Practice - Expii

Multiplying polynomials word problems - examples & practice, explanations (3).

Polynomial Word Problems

Image by geralt via Pixabay ( CC0 )

As of right now, you should know how to add , subtract , and multiply polynomials.

So when we look at word problems they'll only be asking you to add, subtract, or multiply polynomials.

The trickier part is figuring out which they want you to use. Fortunately, the problems usually deal with shapes which can help clue us in on what to use. If it references perimeter, chances are you need to use addition or subtraction. If references area or volume, chances are you need to use multiplication.

Let's look at an example.

Linda has a rectangular garden that's 3x−5 feet by 2x+8 feet. She wants to put a fence around the perimeter of the garden. If each foot of fence costs 5 dollars, how much will the total fencing around the garden cost?

Step 1: Draw a Diagram

Seriously, don't skip this step. Diagrams are a great way to help visualize the problem and keep things in order. Plus you get to make a quick doodle.

Image Source: Expii

Here's Linda's garden. Each side is either 3x−5 feet or 2x+8 feet.

Step 2: Figure out What to Use

We want to find the price of the fencing that will surround the garden. To do this, we first need to figure out how much fencing there is.

This is a perimeter problem. Which means, we'll need to add up the sides.

Step 3: Set up the Problem

The last trickier step, is to set the problem up . First, we need to find the perimeter of the rectangle. perimeter=(3x−5)+(2x+8)+(3x−5)+(2x+8) Then, we multiply this by the price per foot of fencing, which is 5 dollars. 5(perimeter)=5[(3x−5)+(2x+8)+(3x−5)+(2x+8)]

Step 4: Solve

In my opinion, this is the easiest step of word problems. We already have it all set up, and finally we just add together some polynomials which we already know how to do. 5[(3x−5)+(2x+8)+(3x−5)+(2x+8)]=5[3x−5+2x+8+3x−5+2x+8]=5[(3x+2x+3x+2x)+(−5+8−5+8)]=5[10x+6]=50x+30 It will cost 50x+30 dollars to put fencing around this garden.

Related Lessons

Word problems involving binomials are often related to basic geometry (like the concept of area , for example).

An important thing to remember is that word problems are just presenting you with familiar information in a new way (i.e., in words). You already know how to handle these problems , so don't let the fact that they're word problems throw you off.

Let's look at an example:

Image source: by Hannah Bonville

First, let's remind ourselves of how to find area. What's the formula for finding the area of the shape above?

Area=length+width

Area=length×width

Area=(2×length)+(2×width)

Area=length/width

(Video) Polynomials 06 Multiply Polynomials Word Problem

by Mister Zuidema

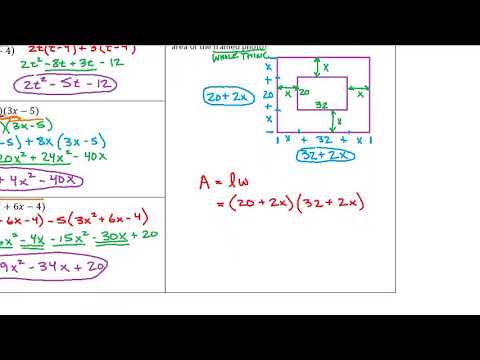
This video by Mister Zuidema walks through a word problem with polynomials.

Let's look at it.

Sally has a photo which is 20 cm tall and 32 cm wide. She wants to put a frame around the photo which is the same width all around. What is the expression for the area of the framed photo.

First, we draw out the diagram of the photo and the frame. We don't know the width of the frame, so we label it x. We want the area of the whole frame, so we need to write an expression that is equal to the length times the height of the frame. We know the photo is 32 cm wide and the frame is x wide on each side. So, the length of the frame is (32+2x). We find the height of the frame similarly. We know the height of the photo is 20 and each side of the frame is x, so the height is (20+2x). Now, the area is the length times the width, so we multiply binomials. In the video, he uses a different way of multiplying, but I will be using FOIL . We see,

(32+2x)×(20+2x)=(32)(20)+(32)(2x)+(2x)(20)+(2x)(2x)=640+64x+40x+4x2=640+104x+4x2

The expression that represents the area of the whole frame is 640+104x+4x2 which is equal to 4x2+104x+640

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Share Podcast

A Better Framework for Solving Tough Problems

Start with trust and end with speed.

• Apple Podcasts

When it comes to solving complicated problems, the default for many organizational leaders is to take their time to work through the issues at hand. Unfortunately, that often leads to patchwork solutions or problems not truly getting resolved.

But Anne Morriss offers a different framework. In this episode, she outlines a five-step process for solving any problem and explains why starting with trust and ending with speed is so important for effective change leadership. As she says, “Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.”

Morriss is an entrepreneur and leadership coach. She’s also the coauthor of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems .

Key episode topics include: strategy, decision making and problem solving, strategy execution, managing people, collaboration and teams, trustworthiness, organizational culture, change leadership, problem solving, leadership.

HBR On Strategy curates the best case studies and conversations with the world’s top business and management experts, to help you unlock new ways of doing business. New episodes every week.

• Listen to the full HBR IdeaCast episode: How to Solve Tough Problems Better and Faster (2023)
• Find more episodes of HBR IdeaCast
• Discover 100 years of Harvard Business Review articles, case studies, podcasts, and more at HBR.org .

HANNAH BATES: Welcome to HBR On Strategy , case studies and conversations with the world’s top business and management experts, hand-selected to help you unlock new ways of doing business.

When it comes to solving complicated problems, many leaders only focus on the most apparent issues. Unfortunately that often leads to patchwork or partial solutions. But Anne Morriss offers a different framework that aims to truly tackle big problems by first leaning into trust and then focusing on speed.

Morriss is an entrepreneur and leadership coach. She’s also the co-author of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems . In this episode, she outlines a five-step process for solving any problem. Some, she says, can be solved in a week, while others take much longer. She also explains why starting with trust and ending with speed is so important for effective change leadership.

This episode originally aired on HBR IdeaCast in October 2023. Here it is.

CURT NICKISCH: Welcome to the HBR IdeaCast from Harvard Business Review. I’m Curt Nickisch.

Problems can be intimidating. Sure, some problems are fun to dig into. You roll up your sleeves, you just take care of them; but others, well, they’re complicated. Sometimes it’s hard to wrap your brain around a problem, much less fix it.

And that’s especially true for leaders in organizations where problems are often layered and complex. They sometimes demand technical, financial, or interpersonal knowledge to fix. And whether it’s avoidance on the leaders’ part or just the perception that a problem is systemic or even intractable, problems find a way to endure, to keep going, to keep being a problem that everyone tries to work around or just puts up with.

But today’s guest says that just compounds it and makes the problem harder to fix. Instead, she says, speed and momentum are key to overcoming a problem.

Anne Morriss is an entrepreneur, leadership coach and founder of the Leadership Consortium and with Harvard Business School Professor Francis Frei, she wrote the new book, Move Fast and Fix Things: The Trusted Leaders Guide to Solving Hard Problems . Anne, welcome back to the show.

ANNE MORRISS: Curt, thank you so much for having me.

CURT NICKISCH: So, to generate momentum at an organization, you say that you really need speed and trust. We’ll get into those essential ingredients some more, but why are those two essential?

ANNE MORRISS: Yeah. Well, the essential pattern that we observed was that the most effective change leaders out there were building trust and speed, and it didn’t seem to be a well-known observation. We all know the phrase, “Move fast and break things,” but the people who were really getting it right were moving fast and fixing things, and that was really our jumping off point. So when we dug into the pattern, what we observed was they were building trust first and then speed. This foundation of trust was what allowed them to fix more things and break fewer.

CURT NICKISCH: Trust sounds like a slow thing, right? If you talk about building trust, that is something that takes interactions, it takes communication, it takes experiences. Does that run counter to the speed idea?

ANNE MORRISS: Yeah. Well, this issue of trust is something we’ve been looking at for over a decade. One of the headlines in our research is it’s actually something we’re building and rebuilding and breaking all the time. And so instead of being this precious, almost farbege egg, it’s this thing that is constantly in motion and this thing that we can really impact when we’re deliberate about our choices and have some self-awareness around where it’s breaking down and how it’s breaking down.

CURT NICKISCH: You said break trust in there, which is intriguing, right? That you may have to break trust to build trust. Can you explain that a little?

ANNE MORRISS:  Yeah, well, I’ll clarify. It’s not that you have to break it in order to build it. It’s just that we all do it some of the time. Most of us are trusted most of the time. Most of your listeners I imagine are trusted most of the time, but all of us have a pattern where we break trust or where we don’t build as much as could be possible.

CURT NICKISCH: I want to talk about speed, this other essential ingredient that’s so intriguing, right? Because you think about solving hard problems as something that just takes a lot of time and thinking and coordination and planning and designing. Explain what you mean by it? And also, just  how we maybe approach problems wrong by taking them on too slowly?

ANNE MORRISS: Well, Curt, no one has ever said to us, “I wish I had taken longer and done less.” We hear the opposite all the time, by the way. So what we really set out to do was to create a playbook that anyone can use to take less time to do more of the things that are going to make your teams and organizations stronger.

And the way we set up the book is okay, it’s really a five step process. Speed is the last step. It’s the payoff for the hard work you’re going to do to figure out your problem, build or rebuild trust, expand the team in thoughtful and strategic ways, and then tell a real and compelling story about the change you’re leading.

Only then do you get to go fast, but that’s an essential part of the process, and we find that either people under emphasize it or speed has gotten a bad name in this world of moving fast and breaking things. And part of our mission for sure was to rehabilitate speed’s reputation because it is an essential part of the change leader’s equation. It can be the difference between good intentions and getting anything done at all.

CURT NICKISCH: You know, the fact that nobody ever tells you, “I wish we had done less and taken more time.” I think we all feel that, right? Sometimes we do something and then realize, “Oh, that wasn’t that hard and why did it take me so long to do it? And I wish I’d done this a long time ago.” Is it ever possible to solve a problem too quickly?

ANNE MORRISS: Absolutely. And we see that all the time too. What we push people to do in those scenarios is really take a look at the underlying issue because in most cases, the solution is not to take your foot off the accelerator per se and slow down. The solution is to get into the underlying problem. So if it’s burnout or a strategic disconnect between what you’re building and the marketplace you’re serving, what we find is the anxiety that people attach to speed or the frustration people attach to speed is often misplaced.

CURT NICKISCH: What is a good timeline to think about solving a problem then? Because if we by default take too long or else jump ahead and we don’t fix it right, what’s a good target time to have in your mind for how long solving a problem should take?

ANNE MORRISS: Yeah. Well, we’re playful in the book and talking about the idea that many problems can be solved in a week. We set the book up five chapters. They’re titled Monday, Tuesday, Wednesday, Thursday, Friday, and we’re definitely having fun with that. And yet, if you count the hours in a week, there are a lot of them. Many of our problems, if you were to spend a focused 40 hours of effort on a problem, you’re going to get pretty far.

But our main message is, listen, of course it’s going to depend on the nature of the problem, and you’re going to take weeks and maybe even some cases months to get to the other side. What we don’t want you to do is take years, which tends to be our default timeline for solving hard problems.

CURT NICKISCH: So you say to start with identifying the problem that’s holding you back, seems kind of obvious. But where do companies go right and wrong with this first step of just identifying the problem that’s holding you back?

ANNE MORRISS: And our goal is that all of these are going to feel obvious in retrospect. The problem is we skip over a lot of these steps and this is why we wanted to underline them. So this one is really rooted in our observation and I think the pattern of our species that we tend to be overconfident in the quality of our thoughts, particularly when it comes to diagnosing problems.

And so we want to invite you to start in a very humble and curious place, which tends not to be our default mode when we’re showing up for work. We convince ourselves that we’re being paid for our judgment. That’s exactly what gets reinforced everywhere. And so we tend to counterintuitively, given what we just talked about, we tend to move too quickly through the diagnostic phase.

CURT NICKISCH: “I know what to do, that’s why you hired me.”

ANNE MORRISS: Exactly. “I know what to do. That’s why you hired me. I’ve seen this before. I have a plan. Follow me.” We get rewarded for the expression of confidence and clarity. And so what we’re inviting people to do here is actually pause and really lean into what are the root causes of the problem you’re seeing? What are some alternative explanations? Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.

CURT NICKISCH: So what do you recommend for this step, for getting to the root of the problem? What are questions you should ask? What’s the right thought process? What do you do on Monday of the week?

ANNE MORRISS: In our experience of doing this work, people tend to undervalue the power of conversation, particularly with other people in the organization. So we will often advocate putting together a team of problem solvers, make it a temporary team, really pull in people who have a particular perspective on the problem and create the space, make it as psychologically safe as you can for people to really, as Chris Argyris so beautifully articulated, discuss the undiscussable.

And so the conditions for that are going to look different in every organization depending on the problem, but if you can get a space where smart people who have direct experience of a problem are in a room and talking honestly with each other, you can make an extraordinary amount of progress, certainly in a day.

CURT NICKISCH: Yeah, that gets back to the trust piece.

ANNE MORRISS: Definitely.

CURT NICKISCH: How do you like to start that meeting, or how do you like to talk about it? I’m just curious what somebody on that team might hear in that meeting, just to get the sense that it’s psychologically safe, you can discuss the undiscussable and you’re also focusing on the identification part. What’s key to communicate there?

ANNE MORRISS: Yeah. Well, we sometimes encourage people to do a little bit of data gathering before those conversations. So the power of a quick anonymous survey around whatever problem you’re solving, but also be really thoughtful about the questions you’re going to ask in the moment. So a little bit of preparation can go a long way and a little bit of thoughtfulness about the power dynamic. So who’s going to walk in there with license to speak and who’s going to hold back? So being thoughtful about the agenda, about the questions you’re asking about the room, about the facilitation, and then courage is a very infectious emotion.

So if you can early on create the conditions for people to show up bravely in that conversation, then the chance that you’re going to get good information and that you’re going to walk out of that room with new insight in the problem that you didn’t have when you walked in is extraordinarily high.

CURT NICKISCH: Now, in those discussions, you may have people who have different perspectives on what the problem really is. They also bear different costs of addressing the problem or solving it. You talked about the power dynamic, but there’s also an unfairness dynamic of who’s going to actually have to do the work to take care of it, and I wonder how you create a culture in that meeting where it’s the most productive?

ANNE MORRISS: For sure, the burden of work is not going to be equitably distributed around the room. But I would say, Curt, the dynamic that we see most often is that people are deeply relieved that hard problems are being addressed. So it really can create, and more often than not in our experience, it does create this beautiful flywheel of action, creativity, optimism. Often when problems haven’t been addressed, there is a fair amount of anxiety in the organization, frustration, stagnation. And so credible movement towards action and progress is often the best antidote. So even if the plan isn’t super clear yet, if it’s credible, given who’s in the room and their decision rights and mandate, if there’s real momentum coming out of that to make progress, then that tends to be deeply energizing to people.

CURT NICKISCH: I wonder if there’s an organization that you’ve worked with that you could talk about how this rolled out and how this took shape?

ANNE MORRISS: When we started working with Uber, that was wrestling with some very public issues of culture and trust with a range of stakeholders internally, the organization, also external, that work really started with a campaign of listening and really trying to understand where trust was breaking down from the perspective of these stakeholders?

So whether it was female employees or regulators or riders who had safety concerns getting into the car with a stranger. This work, it starts with an honest internal dialogue, but often the problem has threads that go external. And so bringing that same commitment to curiosity and humility and dialogue to anyone who’s impacted by the problem is the fastest way to surface what’s really going on.

CURT NICKISCH: There’s a step in this process that you lay out and that’s communicating powerfully as a leader. So we’ve heard about listening and trust building, but now you’re talking about powerful communication. How do you do this and why is it maybe this step in the process rather than the first thing you do or the last thing you do?

ANNE MORRISS: So in our process, again, it’s the days of the week. On Monday you figured out the problem. Tuesday you really got into the sandbox in figuring out what a good enough plan is for building trust. Wednesday, step three, you made it better. You created an even better plan, bringing in new perspectives. Thursday, this fourth step is the day we’re saying you got to go get buy-in. You got to bring other people along. And again, this is a step where we see people often underinvest in the power and payoff of really executing it well.

CURT NICKISCH: How does that go wrong?

ANNE MORRISS: Yeah, people don’t know the why. Human behavior and the change in human behavior really depends on a strong why. It’s not just a selfish, “What’s in it for me?” Although that’s helpful, but where are we going? I may be invested in a status quo and I need to understand, okay, if you’re going to ask me to change, if you’re going to invite me into this uncomfortable place of doing things differently, why am I here? Help me understand it and articulate the way forward and language that not only I can understand, but also that’s going to be motivating to me.

CURT NICKISCH: And who on my team was part of this process and all that kind of stuff?

ANNE MORRISS: Oh, yeah. I may have some really important questions that may be in the way of my buy-in and commitment to this plan. So certainly creating a space where those questions can be addressed is essential. But what we found is that there is an architecture of a great change story, and it starts with honoring the past, honoring the starting place. Sometimes we’re so excited about the change and animated about the change that what has happened before or what is even happening in the present tense is low on our list of priorities.

Or we want to label it bad, because that’s the way we’ve thought about the change, but really pausing and honoring what came before you and all the reasonable decisions that led up to it, I think can be really helpful to getting people emotionally where you want them to be willing to be guided by you. Going back to Uber, when Dara Khosrowshahi came in.

CURT NICKISCH: This is the new CEO.

ANNE MORRISS: The new CEO.

CURT NICKISCH: Replaced Travis Kalanick, the founder and first CEO, yeah.

ANNE MORRISS: Yeah, and had his first all-hands meeting. One of his key messages, and this is a quote, was that he was going to retain the edge that had made Uber, “A force of nature.” And in that meeting, the crowd went wild because this is also a company that had been beaten up publicly for months and months and months, and it was a really powerful choice. And his predecessor, Travis was in the room, and he also honored Travis’ incredible work and investment in bringing the company to the place where it was.

And I would use words like grace to also describe those choices, but there’s also an incredible strategic value to naming the starting place for everybody in the room because in most cases, most people in that room played a role in getting to that starting place, and you’re acknowledging that.

CURT NICKISCH: You can call it grace. Somebody else might call it diplomatic or strategic. But yeah, I guess like it or not, it’s helpful to call out and honor the complexity of the way things have been done and also the change that’s happening.

ANNE MORRISS: Yeah, and the value. Sometimes honoring the past is also owning what didn’t work or what wasn’t working for stakeholders or segments of the employee team, and we see that around culture change. Sometimes you’ve got to acknowledge that it was not an equitable environment, but whatever the worker, everyone in that room is bringing that pass with them. So again, making it discussable and using it as the jumping off place is where we advise people to start.

Then you’ve earned the right to talk about the change mandate, which we suggest using clear and compelling language about the why. “This is what happened, this is where we are, this is the good and the bad of it, and here’s the case for change.”

And then the last part, which is to describe a rigorous and optimistic way forward. It’s a simple past, present, future arc, which will be familiar to human beings. We love stories as human beings. It’s among the most powerful currency we have to make sense of the world.

CURT NICKISCH: Yeah. Chronological is a pretty powerful order.

ANNE MORRISS: Right. But again, the change leaders we see really get it right, are investing an incredible amount of time into the storytelling part of their job. Ursula Burns, the Head of Xerox is famous for the months and years she spent on the road just telling the story of Xerox’s change, its pivot into services to everyone who would listen, and that was a huge part of her success.

CURT NICKISCH: So Friday or your fifth step, you end with empowering teams and removing roadblocks. That seems obvious, but it’s critical. Can you dig into that a little bit?

ANNE MORRISS: Yeah. Friday is the fun day. Friday’s the release of energy into the system. Again, you’ve now earned the right to go fast. You have a plan, you’re pretty confident it’s going to work. You’ve told the story of change the organization, and now you get to sprint. So this is about really executing with urgency, and it’s about a lot of the tactics of speed is where we focus in the book. So the tactics of empowerment, making tough strategic trade-offs so that your priorities are clear and clearly communicated, creating mechanisms to fast-track progress. At Etsy, CEO Josh Silverman, he labeled these projects ambulances. It’s an unfortunate metaphor, but it’s super memorable. These are the products that get to speed out in front of the other ones because the stakes are high and the clock is sticking.

CURT NICKISCH: You pull over and let it go by.

ANNE MORRISS: Yeah, exactly. And so we have to agree as an organization on how to do something like that. And so we see lots of great examples both in young organizations and big complex biotech companies with lots of regulatory guardrails have still found ways to do this gracefully.

And I think we end with this idea of conflict debt, which is a term we really love. Leanne Davey, who’s a team scholar and researcher, and anyone in a tech company will recognize the idea of tech debt, which is this weight the organization drags around until they resolve it. Conflict debt is a beautiful metaphor because it is this weight that we drag around and slows us down until we decide to clean it up and fix it. The organizations that are really getting speed right have figured out either formally or informally, how to create an environment where conflict and disagreements can be gracefully resolved.

CURT NICKISCH: Well, let’s talk about this speed more, right? Because I think this is one of those places that maybe people go wrong or take too long, and then you lose the awareness of the problem, you lose that urgency. And then that also just makes it less effective, right? It’s not just about getting the problem solved as quickly as possible. It’s also just speed in some ways helps solve the problem.

ANNE MORRISS: Oh, yeah. It really is the difference between imagining the change you want to lead and really being able to bring it to life. Speed is the thing that unlocks your ability to lead change. It needs a foundation, and that’s what Monday through Thursday is all about, steps one through four, but the finish line is executing with urgency, and it’s that urgency that releases the system’s energy, that communicates your priorities, that creates the conditions for your team to make progress.

CURT NICKISCH: Moving fast is something that entrepreneurs and tech companies certainly understand, but there’s also this awareness that with big companies, the bigger the organization, the harder it is to turn the aircraft carrier around, right? Is speed relative when you get at those levels, or do you think this is something that any company should be able to apply equally?

ANNE MORRISS: We think this applies to any company. The culture really lives at the level of team. So we believe you can make a tremendous amount of progress even within your circle of control as a team leader. I want to bring some humility to this and careful of words like universal, but we do think there’s some universal truths here around the value of speed, and then some of the byproducts like keeping fantastic people. Your best people want to solve problems, they want to execute, they want to make progress and speed, and the ability to do that is going to be a variable in their own equation of whether they stay or they go somewhere else where they can have an impact.

CURT NICKISCH: Right. They want to accomplish something before they go or before they retire or finish something out. And if you’re able to just bring more things on the horizon and have it not feel like it’s going to be another two years to do something meaningful.

ANNE MORRISS: People – I mean, they want to make stuff happen and they want to be around the energy and the vitality of making things happen, which again, is also a super infectious phenomenon. One of the most important jobs of a leader, we believe, is to set the metabolic pace of their teams and organizations. And so what we really dig into on Friday is, well, what does that look like to speed something up? What are the tactics of that?

CURT NICKISCH: I wonder if that universal truth, that a body in motion stays in motion applies to organizations, right? If an organization in motion stays in motion, there is something to that.

ANNE MORRISS: Absolutely.

CURT NICKISCH: Do you have a favorite client story to share, just where you saw speed just become a bit of a flywheel or just a positive reinforcement loop for more positive change at the organization?

ANNE MORRISS: Yeah. We work with a fair number of organizations that are on fire. We do a fair amount of firefighting, but we also less dramatically do a lot of fire prevention. So we’re brought into organizations that are working well and want to get better, looking out on the horizon. That work is super gratifying, and there is always a component of, well, how do we speed this up?

What I love about that work is there’s often already a high foundation of trust, and so it’s, well, how do we maintain that foundation but move this flywheel, as you said, even faster? And it’s really energizing because often there’s a lot of pent-up energy that… There’s a lot of loyalty to the organization, but often it’s also frustration and pent-up energy. And so when that gets released, when good people get the opportunity to sprint for the first time in a little while, it’s incredibly energizing, not just for us, but for the whole organization.

CURT NICKISCH: Anne, this is great. I think finding a way to solve problems better but also faster is going to be really helpful. So thanks for coming on the show to talk about it.

ANNE MORRISS:  Oh, Curt, it was such a pleasure. This is my favorite conversation. I’m delighted to have it anytime.

HANNAH BATES: That was entrepreneur, leadership coach, and author Anne Morriss – in conversation with Curt Nickisch on HBR IdeaCast.

We’ll be back next Wednesday with another hand-picked conversation about business strategy from Harvard Business Review. If you found this episode helpful, share it with your friends and colleagues, and follow our show on Apple Podcasts, Spotify, or wherever you get your podcasts. While you’re there, be sure to leave us a review.

When you’re ready for more podcasts, articles, case studies, books, and videos with the world’s top business and management experts, you’ll find it all at HBR.org.

This episode was produced by Mary Dooe, Anne Saini, and me, Hannah Bates. Ian Fox is our editor. Special thanks to Rob Eckhardt, Maureen Hoch, Erica Truxler, Ramsey Khabbaz, Nicole Smith, Anne Bartholomew, and you – our listener. See you next week.

• Subscribe On:

Latest in this series

This article is about strategy.

• Decision making and problem solving
• Strategy execution
• Leadership and managing people
• Collaboration and teams
• Trustworthiness
• Organizational culture

Partner Center

Environment | Illegal trash dumping is a problem in Silicon…

Share this:.

• Click to share on Facebook (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to print (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• Click to share on Reddit (Opens in new window)

Today's e-Edition

• Latest News

Environment

• Transportation

Breaking News

Environment | jury deliberations begin in donald trump’s hush money criminal case, environment | illegal trash dumping is a problem in silicon valley. here’s how one south bay town is trying to solve it., with county resources spread thin, san martin residents have taken trash cleanup into their own hands.

He peels the flattened husk of the poor creature off the pavement, to the disgusted groans and laughter of his trash-collecting companions.

The volunteer-led San Martin Trash Bash can add that snake to a list of odd and sometimes unsettling finds that includes hundred-pound tractor tires, porn DVDs and even dead goats.

While litter is an issue all over Silicon Valley, unincorporated San Martin does not have dedicated staff to deal with the problem. So instead, a group of volunteers has taken matters into their own hands, cleaning up 1,300 lbs. of trash in 2024 alone — and that number can stretch into multiple tons by the end of a year.

“We’re unincorporated, we don’t have a governing body that’s local, so we’re the citizenship putting in the time,” said resident Liz Paredes Bahnsen. “This is my home. This is my backyard, this is my front yard. Let’s keep it clean.”

Volunteers Anthony Stafford, left, Tyler Kroen, Paula Bringelson and Connie Ludewig load a truck with trash after picking it up at the intersection of Murphy and San Martin avenues during their bi-annual cleanup event in San Martin, Calif., on Saturday, May 18, 2024. (Ray Chavez/Bay Area News Group)

Volunteer Pamela Courtney picks up trash at the intersection of Murphy and San Martin avenues during their bi-annual cleanup event in San Martin, Calif., on Saturday, May 18, 2024. (Ray Chavez/Bay Area News Group)

Volunteers Anthony Stafford, center, Paula Bringelson, right, and other volunteers unload a truck with trash into a dumpster after picking it up at several locations around the town during their bi-annual cleanup event in San Martin, Calif., on Saturday, May 18, 2024. (Ray Chavez/Bay Area News Group)

Volunteer Jacob Hoefling picks up trash near Llagas Creek during their bi-annual cleanup event in San Martin, Calif., on Saturday, May 18, 2024. (Ray Chavez/Bay Area News Group)

Volunteer Martin Groen picks up trash near Llagas Creek during their bi-annual cleanup event in San Martin, Calif., on Saturday, May 18, 2024. (Ray Chavez/Bay Area News Group)

Volunteer Paula Bringelson picks up trash at the intersection of Murphy and San Martin avenues during their bi-annual cleanup event in San Martin, Calif., on Saturday, May 18, 2024. (Ray Chavez/Bay Area News Group)

The clean-up group began back in 2017 when residents from the San Martin Neighborhood Association were trying to figure out what to do about the trash around San Martin — a rural town tucked between Morgan Hill and Gilroy. While residents could call the county to haul away large objects like furniture or broken-down trailers, everyday litter and debris were left untouched. The town also has a small dump, which some residents say exacerbates the problem when winds blow garbage from the dump, or when individuals who don’t want to pay the fees to legally get rid of their junk decide to drop their load on a back road — which some residents refer to as a “dump and dash.”

“We were brainstorming (about) ‘if the county is not going to clean it up, what can we do?’” said Sharon Luna, who helped lead this year’s Trash Bash.

The association decided to take the problem into their own hands, gathering a few dozen volunteers twice a year to pick up the trash. To sweeten the deal, volunteers get free food, and this year were awarded prizes for the weirdest and largest pieces of trash.

The trash bash has delivered both in volume and weirdness of garbage. The small band of volunteers has gathered tons of trash at their cleanups, peaking at a whopping 7.7 tons in 2019, according to the organizers. In previous years, rubbish has featured a rural flare — including dead goats, dead chickens and tractor tires — as well as satellite dishes, baby booties, a car roof and countless bottles of cheap vodka and Fireball. This year, Kroen’s rattlesnake won for the weirdest find.

However strange the trash might be, San Martin’s garbage problem is far from unique. In 2020, Caltrans reported spending over $100 million cleaning up some 1.3 million bags of trash along state highways. According to Gabe Molina, Superintendent of Roads and Airports for the southern section of the county, trash and illegal dumping are an issue all over Santa Clara County. However, Roads and Airports, which technically has purview over the trash, often lacks the resources to address the garbage problem when they also have to deal with fixing potholes and paving roads while their staff is spread thin.

“It’s really hard for us to send a crew out to go pick up papers when we have bigger scale work to do,” he said. His department helps provide the volunteers with supplies like buckets, garbage bags and safety cones. “I think the unique part about it is for the residents to care enough to volunteer and help clean up.”

This year, a group ranging from a grade-schooler to grandparents gathered along with a contingent from the local volunteer fire brigade to give back to the community by cleaning trash from San Martin’s roadsides and local Llagas Creek.

For many, however, it’s simply a civic duty.

“I have pride in my community. It’s a beautiful area,” says resident Pamela Courtney, standing with the rolling hills of the South Valley behind her. “I want people when they drive through to think that people care about it.”

• Report an error
• Policies and Standards

More in Environment

Environment | California pelicans are starving. Now we think we know why.

Weather | Storms leave widespread wreckage, outages across Texas

Environment | Elusive surfboard-stealing Otter 841 back in Santa Cruz, up to her old tricks

Education | San Jose State professor suspended after pro-Palestinian protest

Trust in AI is more than a moral problem

• Share on Facebook
• Share on LinkedIn

Time's almost up! There's only one week left to request an invite to The AI Impact Tour on June 5th. Don't miss out on this incredible opportunity to explore various methods for auditing AI models. Find out how you can attend here .

The economic potential of AI is uncontested, but it is largely unrealized by organizations, with an astounding 87% of AI projects failing to succeed.

Some consider this a technology problem, others a business problem, a culture problem or an industry problem — but the latest evidence reveals that it is a trust problem.

According to recent research, nearly two-thirds of C-suite executives say that trust in AI drives revenue, competitiveness and customer success.

Trust has been a complicated word to unpack when it comes to AI. Can you trust an AI system ? If so, how? We don’t trust humans immediately, and we’re even less likely to trust AI systems immediately.

June 5th: The AI Audit in NYC

Join us next week in NYC to engage with top executive leaders, delving into strategies for auditing AI models to ensure fairness, optimal performance, and ethical compliance across diverse organizations. Secure your attendance for this exclusive invite-only event.

But a lack of trust in AI is holding back economic potential, and many of the recommendations for building trust in AI systems have been criticized as too abstract or far-reaching to be practical.

It’s time for a new “AI Trust Equation” focused on practical application.

The AI trust equation

The Trust Equation, a concept for building trust between people, was first proposed in The Trusted Advisor by David Maister, Charles Green and Robert Galford. The equation is Trust = Credibility + Reliability + Intimacy, divided by Self-Orientation.

It is clear at first glance why this is an ideal equation for building trust between humans, but it does not translate to building trust between humans and machines.

For building trust between humans and machines , the new AI Trust Equation is Trust = Security + Ethics + Accuracy, divided by Control.

Security forms the first step in the path to trust, and it is made up of several key tenets that are well outlined elsewhere. For the exercise of building trust between humans and machines, it comes down to the question: “Will my information be secure if I share it with this AI system?”

Ethics is more complicated than security because it is a moral question rather than a technical question. Before investing in an AI system, leaders need to consider:

• How were people treated in the making of this model, such as the Kenyan workers in the making of ChatGPT? Is that something I/we feel comfortable with supporting by building our solutions with it?
• Is the model explainable? If it produces a harmful output, can I understand why? And is there anything I can do about it (see Control)?
• Are there implicit or explicit biases in the model? This is a thoroughly documented problem, such as the Gender Shades research from Joy Buolamwini and Timnit Gebru and Google’s recent attempt to eliminate bias in their models, which resulted in creating ahistorical biases .
• What is the business model for this AI system? Are those whose information and life’s work have trained the model being compensated when the model built on their work generates revenue?
• What are the stated values of the company that created this AI system, and how well do the actions of the company and its leadership track to those values? OpenAI’s recent choice to imitate Scarlett Johansson’s voice without her consent, for example, shows a significant divide between the stated values of OpenAI and Altman’s decision to ignore Scarlett Johansson’s choice to decline the use of her voice for ChatGPT.

Accuracy can be defined as how reliably the AI system provides an accurate answer to a range of questions across the flow of work. This can be simplified to: “When I ask this AI a question based on my context, how useful is its answer?” The answer is directly intertwined with 1) the sophistication of the model and 2) the data on which it’s been trained.

Control is at the heart of the conversation about trusting AI, and it ranges from the most tactical question: “Will this AI system do what I want it to do, or will it make a mistake?” to the one of the most pressing questions of our time: “Will we ever lose control over intelligent systems?” In both cases, the ability to control the actions, decisions and output of AI systems underpins the notion of trusting and implementing them.

5 steps to using the AI trust equation

•  Determine whether the system is useful: Before investing time and resources in investigating whether an AI platform is trustworthy, organizations would benefit from determining whether a platform is useful in helping them create more value.
• Investigate if the platform is secure: What happens to your data if you load it into the platform? Does any information leave your firewall? Working closely with your security team or hiring security advisors is critical to ensuring you can rely on the security of an AI system.
• Set your ethical threshold and evaluate all systems and organizations against it: If any models you invest in must be explainable, define, to absolute precision, a common, empirical definition of explainability across your organization, with upper and lower tolerable limits, and measure proposed systems against those limits. Do the same for every ethical principle your organization determines is non-negotiable when it comes to leveraging AI.
• Define your accuracy targets and don’t deviate: It can be tempting to adopt a system that doesn’t perform well because it’s a precursor to human work. But if it’s performing below an accuracy target you’ve defined as acceptable for your organization, you run the risk of low quality work output and a greater load on your people. More often than not, low accuracy is a model problem or a data problem, both of which can be addressed with the right level of investment and focus.
• Decide what degree of control your organization needs and how it’s defined: How much control you want decision-makers and operators to have over AI systems will determine whether you want a fully autonomous system, semi-autonomous, AI-powered, or if your organizational tolerance level for sharing control with AI systems is a higher bar than any current AI systems may be able to reach.

In the era of AI, it can be easy to search for best practices or quick wins, but the truth is: no one has quite figured all of this out yet, and by the time they do, it won’t be differentiating for you and your organization anymore.

So, rather than wait for the perfect solution or follow the trends set by others, take the lead. Assemble a team of champions and sponsors within your organization, tailor the AI Trust Equation to your specific needs, and start evaluating AI systems against it. The rewards of such an endeavor are not just economic but also foundational to the future of technology and its role in society.

Some technology companies see the market forces moving in this direction and are working to develop the right commitments, control and visibility into how their AI systems work — such as with Salesforce’s Einstein Trust Layer — and others are claiming that that any level of visibility would cede competitive advantage. You and your organization will need to determine what degree of trust you want to have both in the output of AI systems as well as with the organizations that build and maintain them.

AI’s potential is immense, but it will only be realized when AI systems and the people who make them can reach and maintain trust within our organizations and society. The future of AI depends on it.

Brian Evergreen is author of “Autonomous Transformation: Creating a More Human Future in the Era of Artificial Intelligence .”

DataDecisionMakers

Welcome to the VentureBeat community!

DataDecisionMakers is where experts, including the technical people doing data work, can share data-related insights and innovation.

If you want to read about cutting-edge ideas and up-to-date information, best practices, and the future of data and data tech, join us at DataDecisionMakers.

You might even consider  contributing an article  of your own!

Read More From DataDecisionMakers

More From Forbes

Oxford geoscience professor myles allen on solving the problem of climate change.

• Share to Facebook
• Share to Twitter
• Share to Linkedin

This week I had the pleasure of meeting Myles Allen . He is Head of Atmospheric, Oceanic and Planetary Physics in the Department of Physics, University of Oxford, and Professor of Geoscience in the School of Geography and Environment. He’s been studying how human and natural influences contribute to climate change since the early 1990s, served on the UN Intergovernmental Panel on Climate Change (IPCC) for its 3rd, 4th and 5th Assessments, and was a Coordinating Lead Author for its special report on 'the impacts of global warming of 1.5 °C above pre-industrial levels,’ and has been dubbed by the BBC “ the physicist behind net zero ”. In short, his scientific credentials regarding climate change are superb.

Professor Myles Allen Delivering The Gresham Lecture on May 21, 2024

But unlike many science professors, Professor Allen is bravely wading into the world of climate policy. The timing of my meeting with Professor Allen was fortuitous. It was the day before he gave a lecture on May 21, 2024, in his capacity as the Frank Jackson Professor of the Environment as part of the annual series of lectures hosted by Gresham College in the City of London. Gresham (b. 1519, d. 1579) was an English merchant, financier, and founder of the Royal Exchange. He started these lectures to ensure the emerging merchant classes were culturally enriched, as well as being versed in the latest science and technology.

The title of Professor Allen’s lecture is “ A Just and Inclusive Net Zero .” You can also view it online , which I highly recommend. The lecture is both global in its ideas and local in terms of the climate change debate taking place in the UK. I am less familiar with this than I am in the United States, and it was through this lens that I read and then listened to his lecture. My overall impression is how pragmatic and non-ideological it is. Professor Allen is no more an apologist for the fossil fuel industry than he is a supporter of the fossil fuel haters. Neither group brings value to the discussion of how to address climate change. Professor Allen does.

Sir Thomas Gresham

While I can’t do justice to his full lecture in this brief summary, here are four points that leaped out to me.

The first is he notes that “in the Paris-aligned scenarios of the IPCC, we are still using fossil fuels, at around one-quarter of the current rate, in 2100, long after the date of net zero.” Today’s world population of eight billion people will have grown to nearly 10 billion, with hopefully a larger percentage leading lives closer to what is enjoyed in the developed world. That means a LOT of fossil fuels. Those who harbor the fantasy that we still have time to achieve our climate goals simply by phasing out fossil fuel use need to get real. “One of the most dangerous myths is that achieving net zero is actually going to be really cheap because carbon-free, instantly-dispatchable energy” will soon take care of all of our energy needs. Nope. Even with the best of battery technologies it will be intermittent, and we’ll need natural gas and nuclear for the baseload.

The Best Beers In Canada According To The Canadian Brewing Awards

Iphone 16 pro max: key new upgrades leaked in latest report, nyt strands 84 hints spangram and answers for sunday may 26th.

People also need to be realistic about some of the barriers to reducing fossil fuel use as rapidly as possible, with permitting being the number one in my mind. Environmentalists protesting transmission lines for bringing renewable power into the grid are part of the problem, not part of the solution. A great local example for me is the Northern Pass project for bringing cheap hydro power from Canada to Massachusetts, which I have written about with John Skjervem, the CIO of Utah Retirement Systems. Permitting extends to domestic mining of the cobalt and rare earths for battery and renewable energy technologies in order to ensure energy security and not being dependent on places like China, Russia, and the Democratic Republic of Congo for getting them.

Second, he calls out what he calls the “climate establishment” filled with those who regard themselves as elite experts who know better than the average citizen what needs to be done, such as “the unelected technocrats like the [UK] Climate Change Committee , the Science-Based Targets Initiative , or the Climate Action Tracker. ” Their perceived arrogance (whether it is real or not doesn’t matter) and disregard for which climate policies will be acceptable to those who will be subject to them is, again, part of the problem, not part of the solution. You can add to that bureaucrats in Brussels. As one example, he drolly quotes the Carbon Border Adjustment Mechanism, “or CBAM, is, in a nutshell, the European Union deciding that it has the right to impose punitive tariffs on imports from countries whose climate policies a team of bureaucrats in Brussels have decided aren’t good enough. I recently heard a talk from one such bureaucrat, I’m sure a very well-intentioned and intelligent chap, in which he said ‘of course, the CBAM is not neo-colonialist.’ If you have to assure people your policy is not neo-colonialist, you have a problem.”

Barnards Inn Hall, Gresham College, Where The Gresham Lecture Is Delivered

Professor Allen rightly suggests that these elite experts should “talking to people who wouldn’t normally show up in their social networks, like populist talk-show hosts, livestock farmers – and the executives of fossil fuel companies.” To that I’d like to add conservatives who are dedicating their lives to addressing climate change. On New Year’s Eve of 2023 I wrote about them and keep finding more. The “Eco-Right” has a very important role to play, and the climate establishment needs to show a little humility (yes, conservatives can have some very good ideas!) and be less self-righteous and start talking to them.

Third, while the “climate establishment” likes to talk about a Just Transition, it largely ignores what is just for the average citizen. Not everyone can go out and replace gas with heat pumps and buy an electric car. Yes, we need to think about a Just Transition for emerging markets, but in the U.S., we also need to think about what this means for low and middle income people in both red and blue states. Professor Allen also provocatively suggests “justice for the fossil fuel industry” which extends beyond “protecting workers in carbon intensive industries, or the interests of new fossil fuel producers, in ways that that just happens, surprise, surprise, to suit the fossil fuel industry itself rather well” to the shareholders of fossil fuel companies and people who benefit from their products—which is pretty much every single one of us.

Justice for the fossil fuel industry means acknowledging its right and need to exist but also holding it accountable for the carbon it produces. As Professor Allen notes, “The greatest climate injustice of all, to my mind, is the fact that the most profitable industry the world has ever known is entirely dependent on selling a product that is causing a very serious problem and no one is even asking them to fix it.” So how to fix it? Here are a few ways that spring to my mind of how not to fix it: (1) divesting from fossil fuel stocks in the naïve belief this will keep them from producing their product (but fine to do so if you don’t believe in the long-term value proposition or you’re just not ethically comfortable holding these stocks), (2) yelling at banks who provide them financing, (3) demanding that fossil fuel companies have unrealistic plans for reducing their investments and production, (4) urging them to get into the renewable energy business (their business model and capabilities don’t lend themselves to this), (5) opposing carbon capture storage technologies using the argument they just prolong the life of the fossil fuel industry, (6) thinking that reporting on Scope 3 emissions will somehow reduce the demand of their customers, and (7) filing useless shareholder proposals using the language of “value creation” to mask a basic hatred of the industry (which all the haters depend on).

Professor Myles Allen: “They just told me to write some physics on the board”

Which gets me to my fourth and last point. What is the solution? “There really is only one way to stop fossil fuels from causing global warming before the world stops using fossil fuels: we have to capture the carbon dioxide they generate and dispose of it, permanently, back underground.” The “underground” part is important. Turning fossil carbon into trees, water, and topsoil only delays its release into the atmosphere. The fossil fuel industry should take responsibility for doing this. It can start modestly, say one percent of the carbon it produces and building up to 100% by 2050. Let’s call this number the “geologically stored fraction.” This is what investors should be focused on, not Scope 3 emissions (although Scope 1 and 2 are fair game). Making this happen will require a mix of regulatory and market forces.

Can this be done? Absolutely. While fossil fuel companies don’t know wind and solar, they for sure know geological carbon management. The industry has a history of innovation and deep technological and engineering expertise for getting fossil fuels out of the ground, which often involving injecting stuff back into the ground. No question in my mind that it can figure out effective and cost efficient ways of putting carbon dioxide back underground at the scale required. In the beginning, the costs of doing so may be so small they just become a cost of doing business and preserving its needed license to operate. Ultimately, the costs will be borne by both the industry and its customers, which includes all of us. But if we want less carbon in the atmosphere but still want to enjoy the benefits of generating it, we must all be willing to pay our fair share for getting rid of it.

• Editorial Standards
• Reprints & Permissions

Join The Conversation

One Community. Many Voices. Create a free account to share your thoughts. 

Forbes Community Guidelines

Our community is about connecting people through open and thoughtful conversations. We want our readers to share their views and exchange ideas and facts in a safe space.

In order to do so, please follow the posting rules in our site's  Terms of Service.   We've summarized some of those key rules below. Simply put, keep it civil.

Your post will be rejected if we notice that it seems to contain:

• False or intentionally out-of-context or misleading information
• Insults, profanity, incoherent, obscene or inflammatory language or threats of any kind
• Attacks on the identity of other commenters or the article's author
• Content that otherwise violates our site's  terms.

User accounts will be blocked if we notice or believe that users are engaged in:

• Continuous attempts to re-post comments that have been previously moderated/rejected
• Racist, sexist, homophobic or other discriminatory comments
• Attempts or tactics that put the site security at risk
• Actions that otherwise violate our site's  terms.

So, how can you be a power user?

• Stay on topic and share your insights
• Feel free to be clear and thoughtful to get your point across
• ‘Like’ or ‘Dislike’ to show your point of view.
• Protect your community.
• Use the report tool to alert us when someone breaks the rules.

Thanks for reading our community guidelines. Please read the full list of posting rules found in our site's  Terms of Service.

The US Army’s drone problem – and how it’s solving it

When the foreign drone swarms come, we’d better hope this works

It’s no secret the US Army has a drone problem . Russia’s wider war on Ukraine, beginning in February 2022, has compelled both sides in the wider conflict to invest heavily in tiny, explosives-laden drones. 

More than two years into the war, the Ukrainians are lobbing as many as 100,000 small drones every month at Russian troops all along the 700-mile front line, a quantity sufficient to overwhelm any army’s existing air defences. It’s not for no reason Russian casualties exceeded 1,700 on May 12 – a record bloody day in the 27-month war.

The Russians are launching only slightly fewer drones – and to only slightly less devastating effect.

Anticipating future battlefields humming with tiny aerial drones , the US Army is scrambling to develop new air-defences that it can deploy in sufficient volume to block swarms of tiny drones. The Army’s main drone-killer, its new M-SHORAD air-defence vehicle, is still years away from large-scale deployment.

So in the meantime, the Army is counting on an interim system: the Mobile-Low, Slow, Small Unmanned Aircraft System Integrated Defeat System – or M-LIDs. 

It’d better work. For a few years, it’s the best defence the world’s leading army can deploy against arguably its biggest threats – tiny drones. 

Happily for the Americans, the M-LIDS – a pair of four-wheel Mine-Resistant All-Terrain Vehicle armored trucks, or M-ATVs, together mounting a missile-launcher, guns, a radar and a drone-grounding radio-jammer – is getting an early workout. A pre-war test, if you will. In Gaza.

When the US Army sailed some of its coastal landing ships to Gaza as part of the US military’s humanitarian flotilla, the ships carried – along with a floating pier for food aid – one of the initial M-LIDS vehicle sets. 

As the humanitarian pier took shape in early May, at least one M-LIDS vehicle rolled down the pier and took up station at the edge of the beach alongside a heavylift truck packing a radar-guided 20-millimetre auto-cannon – a land-based version of the US Navy’s main anti-missile gun .

The M-LIDS is meant to include two vehicles: one armed with Coyote radar-cued anti-drone missiles, and another with a suite of radio-jammers intended to block the signals that connect drones to their controllers on the ground, potentially miles away.

Last Wednesday, a video circulated online depicting the 20-millimetre naval gun engaging a target over the Gaza beach in a test of the humanitarian air-defence system. The M-LIDS didn’t take part in the test; if it did, it might’ve engaged the target drone if and when the gun missed – by attempting to ground the drone by blocking its control signal.

A complete M-LIDS system would include a vehicle with a missile-launcher, meaning it could do more than just ground an incoming drone – it could shoot it down. But even half an M-LIDS could be a significant capability. If it works. And if the Americans can deploy it widely enough to cover front-line forces.

Scale is the main problem. The million-person US Army needs many hundreds, if not thousands, of counter-drone systems to make any difference in a major war. It currently has just a handful that it can deploy alongside a depleted force of Cold War-vintage air-defences.

Apparently aiming to expand M-LIDS coverage ahead of the wider deployment of the more sophisticated M-SHORAD – that’s manoeuvre short-range air defence, for you English-speakers – the Army is combining the main components of the two-vehicle M-LIDS into a single vehicle, an eight-wheel Stryker. 

A 20-ton Stryker is a bigger and more capacious vehicle than a 13-ton M-ATV is. It’s potentially a better counter-drone vehicle. The Army is seeking funding to collapse its drone-defences into a single vehicle, rather than a pair of them, ahead of the wider deployment of improved M-SHORAD vehicles toward the end of the decade.

The single-vehicle M-LIDS might be the US Army’s best bet if a major war breaks out in, say, the next five years – and American brigades must suddenly contend with tens of thousands, or even hundreds of thousands, of tiny enemy drones.

The single set – or half-set – of M-LIDS in Gaza is a small, early test of this drone-defence. Anyone hoping for a Western victory over foreign drone hordes should hope it works.

• Russia-Ukraine invasion live,
• Drones (aircraft),
• Israel-Hamas War,
• Facebook Icon
• WhatsApp Icon

We've detected unusual activity from your computer network

To continue, please click the box below to let us know you're not a robot.

Why did this happen?

Please make sure your browser supports JavaScript and cookies and that you are not blocking them from loading. For more information you can review our Terms of Service and Cookie Policy .

For inquiries related to this message please contact our support team and provide the reference ID below.

Opinion The reward for Republicans who try to solve problems: humiliation

The GOP’s inability to get behind their own border security bill just keeps getting more embarrassing.

Pity poor Sen. James Lankford (R-Okla.), who on Thursday was humiliated into voting against his own border security bill .

Last fall, you might recall, Republican lawmakers refused to pass funding for Ukraine and Israel unless Democrats agreed to “tough” border security measures. Lankford, one of the Senate’s more conservative members, negotiated on the GOP conference’s behalf, and he drove a hard bargain.

Lankford got President Biden and Democrats to agree to revive a version of the controversial Title 42 border expulsion policy, which would shut down much of the asylum system without even the fig leaf of needing a “public health emergency.” It also included more personnel for Customs and Border Protection and Immigration and Customs Enforcement (one reason the major Border Patrol union endorsed it ) and a stricter, faster process for adjudicating asylum claims. Progressives decried many of the asylum measures as inhumane.

Notably, the deal contained none of Democrats’ standard immigration priorities, such as providing permanent legal status for “dreamers,” the young undocumented immigrants brought to the United States as children. So it was pretty much a clean sweep for Republican priorities in exchange for aid to Ukraine and Israel.

We all know what happened next: Former president Donald Trump realized the bill might be too effective at addressing border issues, which the presumed Republican presidential nominee hoped to continue exploiting for political gain heading into the election. So he told his followers to kill their own deal .

Sometimes, alas, a problem is more valuable than its cure.

When Senate Democrats tried to force a vote on the legislation back in February, Republicans blocked it from proceeding. Lankford was one of a handful of Republicans to vote to move the legislation forward at the time and made an impassioned plea for his colleagues to reconsider. He decried misinformation that right-wing pundits had spread about the legislation. He reiterated that a change in law was necessary for dealing with strain on the border and reminded his fellow Republican lawmakers that they had all been sent to Washington to “solve problems.”

As a reward for these problem-solving efforts, Lankford was subsequently censured by party leaders back in his home state.

Later on, Congress passed the Israel and Ukraine aid, unbundled from Republicans’ border demands. So Democrats decided to call Republicans’ bluff, again: On Thursday, Senate Majority Leader Charles E. Schumer (D-N.Y.) held another vote on the border deal, this time with no Democratic quids offered for the Republican quo. Astoundingly, only one Republican senator (Lisa Murkowski of Alaska) voted to advance the bill, despite continued protestations that the border remains in “crisis.”

Ahead of the vote, Republicans explained their objections.

Democrats “own this issue,” said Sen. John Thune (R-S.D.), the minority whip, of ongoing border problems. “I think it’s very clear in people’s minds, this is a Biden problem enabled by Senate Democrats, and therefore [voters are] going to hold Senate Democrats accountable.”

In other words: It’s Democrats’ problem to fix, but I’ll be damned if they try.

Senate Minority Leader Mitch McConnell (R-Ky.), who a few months ago had backed the Lankford-negotiated deal and told his conference to vote for it, voiced similarly cynical opposition. He said he told Biden , “You caused this problem. There is no legislation that allowed the problem to be fixed. Why don’t you just do what the previous administration was doing?”

McConnell neglected to mention, of course, that unlawful border crossings had also spiked under Trump. In 2019, they reached their highest levels in more than a decade, a surge that receded only when a pandemic temporarily disrupted global migration patterns.

More importantly, Biden can’t “just do what the previous administration was doing” on immigration. That’s because Trump’s immigration policies were often illegal.

This is not my own legal judgment. As a regulatory challenge database from the New York University’s Institute for Policy Integrity shows, 94 percent of major Trump-era immigration agency actions that faced legal challenges ultimately did not survive litigation (that is, in 33 out of 35 cases). Either a judge ruled against the agency responsible for the policy, or the agency withdrew the policy after being sued.

In any event, even Lankford voted against advancing his own problem-solving legislation this time. Bizarrely, he blamed Democrats for allegedly forcing his hand, even though it was his own party who had despoiled his bill’s chances of passing.

“It’s trying to score political points rather than actually trying to solve a problem,” Lankford said of Democrats’ attempt to turn his own proposals into law.

You know you’re a great negotiator when you wring concessions out of your opponent and then refuse to accept them.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Applications of Polynomials

• Last updated
• Save as PDF
• Page ID 51466

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Write a polynomial representing the perimeter of a shape
• Write a polynomial representing the area of a surface
• Write a polynomial representing the volume of a solid

Cost, Revenue, and Profit Polynomials

• Write a profit polynomial given revenue and cost polynomials
• Find profit for given quantities produced

In this section we will explore ways that polynomials are used in applications of perimeter, area, and volume. First, we will see how a polynomial can be used to describe the perimeter of a rectangle.

A rectangular garden has one side with a length of \(2x + 3\). Find the perimeter of the garden.

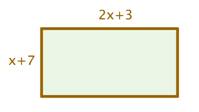
[reveal-answer q=”627193″]Show Solution[/reveal-answer] [hidden-answer a=”627193″]The perimeter of a rectangle is the sum of its side lengths.

\(\left(x+7\right)+\left(2x+3\right)+\left(x+7\right)+\left(2x+3\right)\)

Regroup by like terms.

\(\left(x+2x+x+2x\right)+\left(7+3+7+3\right)\)

Add like terms.

The perimeter is \(6x+20\).

[/hidden-answer]

In the following video you are shown how to find the perimeter of a triangle whose sides are defined as polynomials.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=106

The area of a circle can be found using the radius of the circle and the constant pi in the formula \(A=\pi{r^2}\). In the next example we will use this formula to find a polynomial that describes the area of an irregular shape.

Find a polynomial for the shaded region of the figure.

Read and Understand: We need to find a way to describe the shaded region of this shape using polynomials. We know the formula for the area of a circle is \(A=\pi{r^2}\). The figure we are working with is a circle with a smaller circle cut out.

Define and Translate: The larger circle has radius = r, and the smaller circle has radius= 3. If we find the area of the larger circle, then subtract the area of the smaller circle, the remaining area will be the shaded region. First define the area of the larger circle:

\(A_{1}=\pi{r^2}\)

Then define the area of the smaller circle.

\(A_{2}=\pi{3^2}=9\pi\)

Write and Solve: The shaded region can be found by subtracting the smaller area from the larger area.

\(\begin{array}{c}A_{1}-A_{2}\\=\pi{r^2}-9\pi\end{array}\)

The area of the shaded region is \(\pi{r^2}-9\pi\)

\(\pi{r^2}-9\pi\)

In the video that follows, you will be shown an example of determining the area of a rectangle whose sides are defined as polynomials.

A note about pi.

It is easy to confuse pi as a variable because we use a greek letter to represent it. We use a greek letter instead of a number because nobody has been able to find an end to the number of digits of pi. To be precise and thorough, we use the greek letter as a way to say: “we are including all the digits of pi without having to write them”. The expression for the area of the shaded region in the example above included both the variable r, which represented an unknown radius and the number pi. If we needed to use this expression to build a physical object or instruct a machine to cut specific dimensions, we would round pi to an appropriate number of decimal places.

In the next example, we will write the area for a rectangle in two different ways, one as the product of two binomials and the other as the sum of four rectangles. Because we are describing the same shape two different ways, we should end up with the same expression no matter what way we define the area.

Write two different polynomials that describe the area of of the figure. For one expression, think of the rectangle as one large figure, and for the other expression, think of the rectangle as the sum of 4 different rectangles.

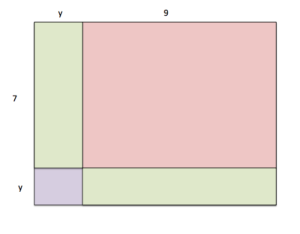
First, we will define the polynomial that describes the area of the rectangle as one figure.

Read and Understand: We are tasked with writing an expressions for the area of the figure above. The area of a rectangle is given as \(A=lw\). We need to consider the whole figure in our dimensions.

Define and Translate: Use the formula for area: \(\begin{array}{c}l=\left(y+7\right)\\w=\left(y+9\right)\end{array}\)

You could define \(\begin{array}{c}w=\left(y+7\right)\\l=\left(y+9\right)\end{array}\) because it doesn’t matter in which order you multiply.

Write and Solve:

\(\begin{array}{c}A=lw\\l=\left(y+7\right)\\w=\left(y+9\right)\end{array}\),

We can use either method we learned to multiply binomials to simplify this expression, we will use a table.

Sum the terms from the table, and simplify:

\(\begin{array}{c}\left(y+7\right)\left(y+9\right)\\=y^2+7y+9y+63\\=y^2+16y+63\end{array}\)

\(A=y^2+16y+63\)

Now we will find an expression for the area of the whole figure as comprised by the areas of the four rectangles added together.

Read and Understand: The area of a rectangle is given as \(A=lw\). We need to first define the areas of each rectangle, then sum them all together to get the area of the whole figure. It helps to label the four rectangle in the figure so you can keep the dimensions organized.

Define and Translate: Use the formula for area: \(A=lw\) for each rectangle:

\(A_{1}=7\cdot{y}\)

\(A_{2}=7\cdot{9}=63\)

\(A_{3}=y\cdot{y}=y^2\)

\(A_{4}=y\cdot{9}\)

\(\begin{array}{c}A=A_{1}+A_{2}+A_{3}+A_{4}\\=7y+63+y^2+9y\\\text{ reorganize and simplify }\\=y^2+16y+63\end{array}\)

Hopefully it isn;t surprising that both expressions simplify to the same thing.

The last example we will provide in this section is one for volume. The volume of regular solids such as spheres, cylinders, cones and rectangular prisms are known. We will find an expression for the volume of a cylinder, which is defined as \(V=\pi{r^2}h\).

Define a polynomial that describes the volume of the cylinder shown in the figure:

Read and Understand: We are tasked with writing an expressions for the volume of the cylinder in the figure above. The volume of a cylinder is given as\(\pi\) is a constant, and r is the radius and h is the height of the cylinder.

Define and Translate: Use the formula for volume:\(V=\pi{r^2}h\), we need to define r and h.

\(\begin{array}{c}r=\left(t-2\right)\\h=7\end{array}\)

Write and Solve: Substitute r and h into the formula for volume.

\(\begin{array}{c}V=\pi{r^2}h\\=\pi\left(t-2\right)^2\cdot{7}\\=7\pi\left({t^2}-2t-2t+4\right)\\=7\pi\left({t^2}-4t+4\right)\end{array}\)

Note that we usually write other constants that are multiplied by \(7\pi\) to each term in the polynomial.

\(\begin{array}{c}7\pi\left({t^2}-4t+4\right)\\=\left(7\pi\right){t^2}-\left(7\pi\right)\cdot{4t}+\left(7\pi\right)\cdot{4}\\=7\pi{t^2}-28\pi{t}+28\pi\end{array}\).

Note again how we left \(\pi\) as a greek letter. If we needed to use this calculation for measurement of materials, we would round pi, or a computer would round for us.

\(V=\pi{r^2}h=7\pi{t^2}-28\pi{t}+28\pi\)

In this last video, we present another example of finding the volume of a cylinder whose dimensions include polynomials.

In the systems of linear equations section, we discussed how a company’s cost and revenue can be modeled with two linear equations. We found that the profit region for a company was the area between the two lines where the company would make money based on how much was produced. In this section, we will see that sometimes polynomials are used to describe cost and revenue.

Profit is typically defined in business as the difference between the amount of money earned (revenue) by producing a certain number of items and the amount of money it takes to produce that number of items. When you are in business, you definitely want to see profit, so it is important to know what your cost and revenue is.

For example, let’s say that the cost to a manufacturer to produce a certain number of things is C and the revenue generated by selling those things is R. The profit, P, can then be defined as

The example we will work with is a hypothetical cell phone manufacturer whose cost to manufacture x number of phones is \(R=-0.09x^2+7000x\).

Define a Profit polynomial for the hypothetical cell phone manufacturer. [reveal-answer q=”50187″]Show Solution[/reveal-answer] [hidden-answer a=”50187″]

Read and Understand: Profit is the difference between revenue and cost, so we will need to define P = R – C for the company.

Define and Translate: \(\begin{array}{c}R=-0.09x^2+7000x\\C=2000x+750,000\end{array}\)

Write and Solve: Substitute the expressions for R and C into the Profit equation.

\(\begin{array}{c}P=R-C\\=-0.09x^2+7000x-\left(2000x+750,000\right)\\=-0.09x^2+7000x-2000x-750,000\\=-0.09x^2+5000x-750,000\end{array}\)

Remember that when you subtract a polynomial, you have to subtract every term of the polynomial.

\(P=-0.09x^2+5000x-750,000\)

Mathematical models are great when you use them to learn important information. The cell phone manufacturing company can use the profit equation to find out how much profit they will make given x number of phones are manufactured. In the next example, we will explore some profit values for this company.

Given the following numbers of cell phones manufactured, find the profit for the cell phone manufacturer:

• x = 100 phones
• x = 25,000 phones
• x=60,000 phones

Interpret your results. [reveal-answer q=”398706″]Show Solution[/reveal-answer] [hidden-answer a=”398706″]

Read and Understand: The profit polynomial defined in the previous example,\(P=-0.09x^2+5000x-750,000\), gives profit based on x number of phones manufactured. We need to substitute the given numbers of phones manufactured into the equation, then try to understand what our answer means in terms of profit and number of phones manufactured.

We will move straight into write and solve since we already have our polynomial. It is probably easiest to use a calculator since the numbers in this problem are so large.

Substitute x = 100

\(\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(100\right)^2+5000\left(100\right)-750,000\\=-900+500,000-750,000\\=-250,900\end{array}\)

Interpret: When the number of phones manufactured is 100, the profit for the business is $-250,000. This is not what we want! The company must produce more than 100 phones to make a profit.

Substitute x = 25,000

\(\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(25000\right)^2+5000\left(25000\right)-750,000\\=-6120000+125,000,000-750,000\\=118,130,000\end{array}\)

Interpret: When the number of phones manufactured is 25,000, the profit for the business is $118,130,000. This is more like it! If the company makes 25,000 phones it will make a profit after it pays all it’s bills.

If this is true, then the company should make even more phones so it can make even more money, right? Actually, something different happens as the number of items manufactured increases without bound.

Substitute x = 60,000

\(\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(60000\right)^2+5000\left(60000\right)-750,000\\=-324,000,000+300,000,000-750,000\\=-24,750,000\end{array}\)

Interpret: When the number of phones manufactured is 60,000, the profit for the business is $-24,750,000. Wait a minute! If the company makes 60,000 phones it will lose money, what happened? At some point, the cost to manufacture the phones will overcome the amount of profit that the business can make. If this is interesting to you, you may enjoy reading about Economics and Business models.

In the video that follows, we present another example of finding a polynomial profit equation.

We have shown that profit can be modeled with a polynomial, and that the profit a company can make based on a business model like this has it’s bounds.

In this section we defined polynomials that represent perimeter, area and volume of well-known shapes. We also introduced some convention about how to use and write \(\pi\) when it is combined with other constants and variables. The next application will introduce you to cost and revenue polynomials. We explored cost and revenue equations in the module on Systems of Linear Equations, now we will see that they can be more than just linear equations, they can be polynomials.

• Screenshot PI. Provided by : Lumen Learning. License : CC BY: Attribution
• Polynomial Multiplication Application - Volume of a Cylinder. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/g-g_nSsfGs4 . License : CC BY: Attribution
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Polynomial Subtracton App - Profit Equation from Revene and Cost. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/-TWjDC4g9dU . License : CC BY: Attribution
• Screenshot: Cell Phones. Provided by : Lumen Learning. License : CC BY: Attribution
• Profit Polynomial Examples. Provided by : Lumen Learning. License : CC BY: Attribution
• Ex: Polynomial Addition Application - Perimeter. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/BhRpZv0_0jE . License : CC BY: Attribution
• Ex: Find the Area of a Rectangle Using a Polynomial. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/5Q2htATOIik . License : CC BY: Attribution
• Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/ . License : CC BY: Attribution
• Applied Optimization Problems. Provided by : OpenStax CNX. Located at : http://cnx.org/contents/svyieFe9@2/Applied-Optimization-Problems . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike . License Terms : Download for free at http://cnx.org/contents/b2fca278-57b...21f539b4cc6f@2

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

Whales Have an Alphabet

Until the 1960s, it was uncertain whether whales made any sounds at all..

This transcript was created using speech recognition software. While it has been reviewed by human transcribers, it may contain errors. Please review the episode audio before quoting from this transcript and email [email protected] with any questions.

[MUSIC PLAYING]

From “The New York Times,” I’m Michael Barbaro. This is “The Daily.”

Today, ever since the discovery that whales produce songs, scientists have been trying to find a way to decipher their lyrics. After 60 years, they may have finally done it. My colleague, Carl Zimmer, explains.

It’s Friday, May 24.

I have to say, after many years of working with you on everything from the pandemic to —

— CRISPR DNA technology, that it turns out your interests are even more varied than I had thought, and they include whales.

They do indeed.

And why? What is it about the whale that captures your imagination?

I don’t think I’ve ever met anybody who is not fascinated by whales. I mean, these are mammals like us, and they’re swimming around in the water. They have brains that are much bigger than ours. They can live maybe 200 years. These are incredible animals, and animals that we still don’t really understand.

Right. Well, it is this majestic creature that brings us together today, Carl, because you have been reporting on a big breakthrough in our understanding of how it is that whales communicate. But I think in order for that breakthrough to make sense, I think we’re going to have to start with what we have known up until now about how whales interact. So tell us about that.

Well, people knew that whales and dolphins traveled together in groups, but up until the 1960s, we didn’t really know that whales actually made any sounds at all. It was actually sort of an accident that we came across it. The American military was developing sophisticated microphones to put underwater. They wanted to listen for Russian submarines.

As one does. But there was an engineer in Bermuda, and he started hearing some weird stuff.

[WHALE SOUNDS]

And he wondered maybe if he was actually listening to whales.

What made him wonder if it was whales, of all things?

Well, this sound did not sound like something geological.

It didn’t sound like some underwater landslide or something like that. This sounded like a living animal making some kind of call. It has these incredible deep tones that rise up into these strange, almost falsetto type notes.

It was incredibly loud. And so it would have to be some really big animal. And so with humpback whales swimming around Bermuda, this engineer thought, well, maybe these are humpback whales.

And so he gets in touch with a husband and wife team of whale biologists, Roger and Katy Payne, and plays these recordings to them. And they’re pretty convinced that they’re hearing whales, too. And then they go on to go out and confirm that by putting microphones in the water, chasing after groups of whales and confirming, yes, indeed, that these sounds are coming from these humpback whales.

So once these scientists confirm in their minds that these are the sounds of a whale, what happens with this discovery?

Well, Roger and Katy Payne and their colleagues are astonished that this species of whale is swimming around singing all the time for hours on end. And it’s so inspirational to them that they actually help to produce a record that they release “The Song of the Humpback Whale” in 1970.

And so this is being sold in record stores, you know, along with Jimi Hendrix and Rolling Stones. And it is a huge hit.

Yeah, it sells like two million copies.

Well, at the time, it was a huge cultural event. This record, this became almost like an anthem of the environmental movement. And it led, for whales in particular, to a lot of protections for them because now people could appreciate that whales were a lot more marvelous and mysterious than they maybe had appreciated before.

And so you have legislation, like the Marine Mammal Act. The United States just agrees just to stop killing whales. It stops its whaling industry. And so you could argue that the discovery of these whale songs in Bermuda led to at least some species of whales escaping extinction.

Well, beyond the cultural impact of this discovery, which is quite meaningful, I wonder whether scientists and marine biologists are figuring out what these whale songs are actually communicating.

So the Paynes create a whole branch of science, the study of whale songs. It turns out that pretty much every species of whale that we know of sings in some way or another. And it turns out that within a species, different groups of whales in different parts of the world may sing with a different dialect. But the big question of what these whales are singing, what do these songs mean, that remains elusive into the 21st century. And things don’t really change until scientists decide to take a new look at the problem in a new way.

And what is that new way?

So in 2020, a group of whale biologists, including Roger Payne, come together with computer scientists from MIT. Instead of humpback whales, which were the whales where whale songs are first discovered, these scientists decide to study sperm whales in the Caribbean. And humpback whales and sperm whales have very, very different songs. So if you’re used to humpback whales with their crazy high and low singing voices —

Right, those best-selling sounds.

— those are rockin’ tunes of the humpback whales, that’s not what sperm whales do. Sperm whales have a totally different way of communicating with each other. And I actually have some recordings that were provided by the scientists who have been doing this research. And so we can take a listen to some of them.

Wow, It’s like a rhythmic clicking.

These are a group of sperm whales swimming together, communicating.

So whale biologists knew already that there was some structure to this sound. Those clicks that you hear, they come in little pulses. And each of those pulses is known as a coda. And whale biologists had given names to these different codas. So, for example, they call one coda, one plus one plus three —

— which is basically click, click, click, click, click, or four plus three, where you have four clicks in a row and a pause and then three clicks in a row.

Right. And the question would seem to be, is this decipherable communication, or is this just whale gibberish?

Well, this is where the computer scientists were able to come in and to help out. The whale biologists who were listening to the codas from the sperm whales in the Caribbean, they had identified about 21 types. And then that would seem to be about it.

But then, an MIT computer science graduate student named Prajusha Sharma was given the job of listening to them again.

And what does she hear?

In a way, it’s not so much what she heard, but what she saw.

Because when scientists record whale songs, you can look at it kind of like if you’re looking at an audio of a recording of your podcast, you will see the little squiggles of your voice.

And so whale biologists would just look at that ticker of whale songs going across the screen and try to compare them. And Sharma said, I don’t like this. I just — this is not how I look at data. And so what she decided to do is she decided to kind of just visualize the data differently. And essentially, she just kind of flipped these images on their side and saw something totally new.

And what she saw was that sperm whales were singing a whole bunch of things that nobody had actually been hearing.

One thing that she discovered was that you could have a whale that was producing a coda over and over and over again, but it was actually playing with it. It was actually stretching out the coda,

[CLICKING] So to get a little bit longer and a little bit longer, a little bit longer.

And then get shorter and shorter and shorter again. They could play with their codas in a way that nobody knew before. And she also started to see that a whale might throw in an extra click at the end of a coda. So it would be repeating a coda over and over again and then boom, add an extra one right at the end. What they would call an ornamentation. So now, you have yet another signal that these whales are using.

And if we just look at what the sperm whales are capable of producing in terms of different codas, we go from just 21 types that they had found in the Caribbean before to 156. So what the scientists are saying is that what we might be looking at is what they call a sperm whale phonetic alphabet.

Yeah, that’s a pretty big deal because the only species that we know of for sure that has a phonetic alphabet —

— is us, exactly. So the reason that we can use language is because we can make a huge range of sounds by just doing little things with our mouths. A little change in our lips can change a bah to a dah. And so we are able to produce a set of phonetic sounds. And we put those sounds together to make words.

So now, we have sperm whales, which have at least 150 of these different versions of sounds that they make just by making little adjustments to the existing way that they make sounds. And so you can make a chart of their phonetic alphabet, just like you make a chart of the human phonetic alphabet.

So then, that raises the question, do they combine their phonetic alphabet into words? Do they combine their words into sentences? In other words, do sperm whales have a language of their own?

Right. Are they talking to each other, really talking to each other?

If we could really show that whales had language on par with humans, that would be like finding intelligent life on another planet.

We’ll be right back.

So, Carl, how should we think about this phonetic alphabet and whether sperm whales are actually using it to talk to each other?

The scientists on this project are really careful to say that these results do not definitively prove what these sperm whale sounds are. There are a handful of possibilities here in terms of what this study could mean. And one of them is that the whales really are using full-blown language.

What they might be talking about, we don’t know. I mean, perhaps they like to talk about their travels over hundreds and thousands of miles. Maybe they’re talking about, you know, the giant squid that they caught last night. Maybe they’re gossiping about each other.

And you have to remember, sperm whales are incredibly social animals. They have relationships that last for decades. And they live in groups that are in clans of thousands of whales. I mean, imagine the opportunities for gossip.

These are all at least imaginable now. But it’s also possible that they are communicating with each other, but in a way that isn’t language as we know it. You know, maybe these sounds that they’re producing don’t add up to sentences. There’s no verb there. There’s no noun. There’s no structure to it in terms of how we think of language.

But maybe they’re still conveying information to each other. Maybe they’re somehow giving out who they are and what group they belong to. But it’s not in the form of language that we think of.

Right. Maybe it’s more kind of caveman like as in whale to whale, look, there, food.

It’s possible. But, you know, other species have evolved in other directions. And so you have to put yourself in the place of a sperm whale. You know, so think about this. They are communicating in the water. And actually, like sending sounds through water is a completely different experience than through the air like we do.

So a sperm whale might be communicating to the whale right next to it a few yards away, but it might be communicating with whales miles away, hundreds of miles away. They’re in the dark a lot of the time, so they don’t even see the whales right next to them. So it’s just this constant sound that they’re making because they’re in this dark water.

So we might want to imagine that such a species would talk the way we do, but there are just so many reasons to expect that whatever they’re communicating might be just profoundly different, so different that it’s actually hard for us to imagine. And so we need to really, you know, let ourselves be open to lots of possibilities.

And one possibility that some scientists have raised is that maybe language is just the wrong model to think about. Maybe we need to think about music. You know, maybe this strange typewriter, clickety clack is actually not like a Morse code message, but is actually a real song. It’s a kind of music that doesn’t necessarily convey information the way conversation does, but it brings the whales together.

In humans, like, when we humans sing together in choruses, it can be a very emotional experience. It’s a socially bonding experience, but it’s not really like the specific words that we’re singing that bring us together when we’re singing. It’s sharing the music together.

But at a certain point, we stop singing in the chorus, and we start asking each other questions like, hey, what are you doing for dinner? How are you going to get home? There’s a lot of traffic on the BQE. So we are really drawn to the possibility that whales are communicating in that same kind of a mode.

We’re exchanging information. We’re seeking out each other’s well-being and emotional state. And we’re building something together.

And I think that happens because, I mean, language is so fundamental to us as human beings. I mean, it’s like every moment of our waking life depends on language. We are talking to ourselves if we’re not talking to other people.

In our sleep, we dream, and there are words in our dreams. And we’re just stewing in language. And so it’s really, really hard for us to understand how other species might have a really complex communication system with hundreds of different little units of sound that they can use and they can deploy. And to think anything other than, well, they must be talking about traffic on the BQE. Like —

— we’re very human-centric. And we have to resist that.

So what we end up having here is a genuine breakthrough in our understanding of how whales interact. And that seems worth celebrating in and of itself. But it really kind of doubles as a lesson in humility for us humans when it comes to appreciating the idea that there are lots of non-human ways in which language can exist.

That’s right. Humility is always a good idea when we’re thinking about other animals.

So what now happens in this realm of research? And how is it that these scientists, these marine biologists and these computer scientists are going to try to figure out what exactly this alphabet amounts to and how it’s being used?

So what’s going to happen now is a real sea change in gathering data from whales.

So to speak.

So these scientists are now deploying a new generation of undersea microphones. They’re using drones to follow these whales. And what they want to do is they want to be recording sounds from the ocean where these whales live 24 hours a day, seven days a week. And so the hope is that instead of getting, say, a few 100 codas each year on recording, these scientists want to get several hundred million every year, maybe billions of codas every year.

And once you get that much data from whales, then you can start to do some really amazing stuff with artificial intelligence. So these scientists hope that they can use the same kind of artificial intelligence that is behind things like ChatGPT or these artificial intelligence systems that are able to take recordings of people talking and transcribing them into text. They want to use that on the whale communication.

They want to just grind through vast amounts of data, and maybe they will discover more phonetic letters in this alphabet. Who knows? Maybe they will actually find bigger structures, structures that could correspond to language.

If you go really far down this route of possibilities, the hope is that you would understand what sperm whales are saying to each other so well that you could actually create artificial sperm whale communication, and you could play it underwater. You could talk to the sperm whales. And they would talk back. They would react somehow in a way that you had predicted. If that happens, then maybe, indeed, sperm whales have something like language as we understand it.

And the only way we’re going to figure that out is if we figure out not just how they talk to themselves, but how we can perhaps talk to them, which, given everything we’ve been talking about here, Carl, is a little bit ironic because it’s pretty human-centric.

That’s right. This experiment could fail. It’s possible that sperm whales don’t do anything like language as we know it. Maybe they’re doing something that we can’t even imagine yet. But if sperm whales really are using codas in something like language, we are going to have to enter the conversation to really understand it.

Well, Carl, thank you very much. We appreciate it.

Thank you. Sorry. Can I say that again? My voice got really high all of a sudden.

A little bit like a whale’s. Ooh.

Yeah, exactly. Woot. Woot.

Thank yoooo. No. Thank you.

Here’s what else you need to know today.

We allege that Live Nation has illegally monopolized markets across the live concert industry in the United States for far too long. It is time to break it up.

On Thursday, the Justice Department sued the concert giant Live Nation Entertainment, which owns Ticketmaster, for violating federal antitrust laws and sought to break up the $23 billion conglomerate. During a news conference, Attorney General Merrick Garland said that Live Nation’s monopolistic tactics had hurt the entire industry of live events.

The result is that fans pay more in fees, artists have fewer opportunities to play concerts, smaller promoters get squeezed out, and venues have fewer real choices.

In a statement, Live Nation called the lawsuit baseless and vowed to fight it in court.

A reminder — tomorrow, we’ll be sharing the latest episode of our colleagues’ new show, “The Interview.” This week on “The Interview,” Lulu Garcia-Navarro talks with Ted Sarandos, the CEO of Netflix, about his plans to make the world’s largest streaming service even bigger.

I don’t agree with the premise that quantity and quality are somehow in conflict with each other. I think our content and our movie programming has been great, but it’s just not all for you.

Today’s episode was produced by Alex Stern, Stella Tan, Sydney Harper, and Nina Feldman. It was edited by MJ Davis, contains original music by Pat McCusker, Dan Powell, Elisheba Ittoop, Marion Lozano, and Sophia Lanman, and was engineered by Alyssa Moxley. Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly.

Special thanks to Project SETI for sharing their whale recordings.

That’s it for “The Daily.” I’m Michael Barbaro. See you on Tuesday after the holiday.

• May 29, 2024   •   29:46 The Closing Arguments in the Trump Trial
• May 28, 2024   •   25:56 The Alitos and Their Flags
• May 24, 2024   •   25:18 Whales Have an Alphabet
• May 23, 2024   •   34:24 I.C.C. Prosecutor Requests Warrants for Israeli and Hamas Leaders
• May 22, 2024   •   23:20 Biden’s Open War on Hidden Fees
• May 21, 2024   •   24:14 The Crypto Comeback
• May 20, 2024   •   31:51 Was the 401(k) a Mistake?
• May 19, 2024   •   33:23 The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’
• May 17, 2024   •   51:10 The Campus Protesters Explain Themselves
• May 16, 2024   •   30:47 The Make-or-Break Testimony of Michael Cohen
• May 15, 2024   •   27:03 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.

Hosted by Michael Barbaro

Featuring Carl Zimmer

Produced by Alex Stern ,  Stella Tan ,  Sydney Harper and Nina Feldman

Edited by MJ Davis Lin

Original music by Elisheba Ittoop ,  Dan Powell ,  Marion Lozano ,  Sophia Lanman and Pat McCusker

Engineered by Alyssa Moxley

Listen and follow The Daily Apple Podcasts | Spotify | Amazon Music | YouTube

Ever since the discovery of whale songs almost 60 years ago, scientists have been trying to decipher the lyrics.

But sperm whales don’t produce the eerie melodies sung by humpback whales, sounds that became a sensation in the 1960s. Instead, sperm whales rattle off clicks that sound like a cross between Morse code and a creaking door. Carl Zimmer, a science reporter, explains why it’s possible that the whales are communicating in a complex language.

On today’s episode

Carl Zimmer , a science reporter for The New York Times who also writes the Origins column .

Background reading

Scientists find an “alphabet” in whale songs.

These whales still use their vocal cords. But how?

There are a lot of ways to listen to The Daily. Here’s how.

We aim to make transcripts available the next workday after an episode’s publication. You can find them at the top of the page.

The Daily is made by Rachel Quester, Lynsea Garrison, Clare Toeniskoetter, Paige Cowett, Michael Simon Johnson, Brad Fisher, Chris Wood, Jessica Cheung, Stella Tan, Alexandra Leigh Young, Lisa Chow, Eric Krupke, Marc Georges, Luke Vander Ploeg, M.J. Davis Lin, Dan Powell, Sydney Harper, Mike Benoist, Liz O. Baylen, Asthaa Chaturvedi, Rachelle Bonja, Diana Nguyen, Marion Lozano, Corey Schreppel, Rob Szypko, Elisheba Ittoop, Mooj Zadie, Patricia Willens, Rowan Niemisto, Jody Becker, Rikki Novetsky, John Ketchum, Nina Feldman, Will Reid, Carlos Prieto, Ben Calhoun, Susan Lee, Lexie Diao, Mary Wilson, Alex Stern, Dan Farrell, Sophia Lanman, Shannon Lin, Diane Wong, Devon Taylor, Alyssa Moxley, Summer Thomad, Olivia Natt, Daniel Ramirez and Brendan Klinkenberg.

Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly. Special thanks to Sam Dolnick, Paula Szuchman, Lisa Tobin, Larissa Anderson, Julia Simon, Sofia Milan, Mahima Chablani, Elizabeth Davis-Moorer, Jeffrey Miranda, Renan Borelli, Maddy Masiello, Isabella Anderson and Nina Lassam.

Carl Zimmer covers news about science for The Times and writes the Origins column . More about Carl Zimmer

Advertisement