research paper on demographic transition

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 03 November 2015

The demographic transition and economic growth: implications for development policy

• Shyam Ranganathan 1 ,
• Ranjula Bali Swain 2 &
• David JT Sumpter 1  

Palgrave Communications volume  1 , Article number:  15033 ( 2015 ) Cite this article

67k Accesses

19 Citations

28 Altmetric

Metrics details

• Development studies
• Social policy

An important transition in the economic history of countries occurs when they move from a regime of low prosperity, high child mortality and high fertility to a state of high prosperity, low child mortality and low fertility. Researchers have proposed various theories to explain this demographic transition and its relation to economic growth. In this article, we test the validity of some of these theories by fitting a non-linear dynamic model for the available cross-country data. Our approach fills the gap between the micro-level models that discuss causative mechanisms but do not consider if alternative models may fit the data well, and models from growth econometrics that show the impact of different factors on economic growth but do not include non-linearities and complex interactions. In our model, mortality and fertility decline and economic growth are endogenized by considering a simultaneous system of equations in the change variables. The model shows that the transition is best described in terms of a development cycle involving child mortality, fertility and GDP per capita. Fertility rate decreases when child mortality is low, and is weakly dependent on GDP. As fertility rates fall, GDP increases, and as GDP increases, child mortality falls. We further test the hypothesis that female education drives down fertility rates rather than child mortality, but find only weak evidence for it. The Bayesian methodology we use ensures robust models and we identify non-linear interactions between indicators to capture real-world non-linearities. Hence, our models can be used in policymaking to predict short-term evolutions in the indicator variables. We also discuss how our approach can be used to evaluate policy initiatives such as the Millennium Development Goals or the Sustainable Development Goals and set more accurate, country-specific development targets.

Similar content being viewed by others

Multidecadal dynamics project slow 21st-century economic growth and income convergence

Declining population and GDP growth

Facilitating fertility decline through economic development: a principal-agent analysis of local bureaucratic incentives in China’s fertility transition

Introduction.

The Industrial Revolution that brought unprecedented economic growth to Western Europe and North America also coincided with a new epoch in population dynamics ( Galor, 2005 ). Countries moved from a regime of high mortality and high fertility to a regime of low mortality and low fertility, a process that researchers call the demographic transition ( Kalemli-Ozcan, 2002 ). A key question for economists is whether economic growth causes the demographic transition or vice versa. In this article, we address this question by looking at the relationship between child mortality, fertility and economic growth.

One part of the relationship between economic growth and demography is clear. There is evidence of the impact of economic growth on child mortality: looking across all countries, there is a strong negative correlation between a country’s income per capita and child mortality ( Cutler et al., 2006 ). So while inequalities and corruption may cause distortions due to inefficiencies and wastage of resources ( Filmer and Pritchett, 1999 ; Rajkumar and Swaroop, 2008 ), the general pattern is that more money tends to produce better health-care systems. It is plausible that child mortality also impacts economic growth. For example, Heckman and Walker (1990) showed that the return to human capital is highest before the age of 5 years.

The relationship between the other socio-economic indicators is more complicated. Exogenous child mortality decline should lead to a fertility decline as women have fewer children if they know the chance of their survival is high ( Kalemli-Ozcan, 2002 ). But there are many caveats due to specific factors ( Ben-Porath, 1976 ; Barro, 1991 ; Haines, 1998 ). For instance, if the loss of a child affects the mother’s health, there may be a subsequent fertility decline following from a child mortality increase ( Rutstein and Medica, 1978 ). Moreover, families make sequential fertility choice decisions, accounting for the gender and health of surviving children, before choosing to have more children ( Sah, 1991 ; Wolpin, 1997 ).

Economic growth might also directly influence fertility decisions. In the classic Barro–Becker model ( Becker, 1981 ; Barro and Becker, 1989 ), fertility choice is due to opportunity costs as increased wages for women result in less time spent on child bearing and child rearing. The Barro–Becker model has been highly influential and extended by others ( Tamura, 1996 ; Strulik, 2004 ). Empirically its predictions are confirmed for Swedish fertility data ( Eckstein et al., 1999 ), which show that two-thirds of fertility decline can be explained by child mortality decline and the remaining one-third can be explained by increase in wages. More broadly, using a quality–quantity trade-off model, Kögel and Prskawetz (2001) and Tamura (2002) show that an endogenous switch from an agricultural to a manufacturing economy has implications for fertility, which explains the coincidence of industrialization with fertility and mortality declines in countries.

The impact of fertility choice decisions at the individual level on country-level economic growth have proved difficult to quantify. Cigno (1998) proposed that at low development “death-reducing public expenditures are most effective”, but at high development these “crowd out parental expenditures and result in fertility decline”. However, Kalemli-Ozcan (2002 , 2003) shows that the importance of fertility choice under uncertainty of child survival could explain empirical observations of the demographic transition of a wide range of countries. Moreover, Strulik (2004) suggests that child quality expenditures can initiate economic take-offs and result in perpetual growth, while its absence may cause economic stagnation with high fertility. Similarly, Galor (2005) and co-workers ( Galor and Weil, 1996 , 1999 ; Galor and Moav, 2002 ) suggest that the quality–quantity trade-off is endogenously triggered by technological progress, which leads to an increase in returns to education.

In spite of the insights that theoretical models bring, discussions about the underlying mechanisms tend to be “open-ended” ( Brock et al., 2007 ). It is not clear if alternative models may fit observations better. On the other hand, the econometrics approach advocated by Durlauf et al. (2005) and Brock et al. (2007) focuses primarily on economic growth and includes the demographic transition only insofar as it impacts this growth. For instance, in the Barro regressions literature ( Barro, 1991 ), life expectancy (which increases with exogenous child mortality decline) is an important covariate of economic growth. Similarly, using a Bayesian approach and a large number of covariates, Sala-i Martin (1997) , Fernandez et al. (2001) and Ley and Steel (2009) , among others, study the causes of economic growth with some thoroughness and show the importance of life expectancy (and, by implication, child mortality) in explaining economic growth in countries. However, these analyses ignore non-linearities and the complex interactions that are essential features of the process.

Our approach fills the gap between the detailed mechanistic models (for example, Kalemli-Ozcan, 2002 ; Galor, 2005 ; Kögel and Prskawetz, 2001 ; Barro and Becker, 1989 ) and the growth econometric models (for example, Barro, 1991 ; Durlauf et al., 2005 ; Sala-i Martin, 1997 ) in explaining the demographic transition. We fit polynomial models of changes in the key state variables (economic growth, child mortality decline and fertility decline), where each polynomial term represents a specific mechanism through which the change takes place. The non-linear and interaction terms model complex mechanisms beyond just linear correlations. We show that the three key variables of child mortality, fertility rate and GDP are linked to each other in the form of a development cycle.

On the theoretical side, our approach provides a broader appreciation of the non-linearities and interaction effects that are an integral part of complex socio-economic processes such as the demographic transition. On the policymaking side, our approach ensures that the models are robust and useful in short-run scenarios because we model yearly changes as a function of the interactions between the variables of interest. This provides policymakers effective decision-making tools on a yearly basis while remaining flexible enough to incorporate new data that become available over time.

The key results we obtain in this article are as follows. Our model shows that economic growth does not directly impact the fertility rate, but influences it through the intermediate variable child mortality. Similarly, the fertility rate affects child mortality only indirectly by increasing or decreasing the economic growth. These conclusions are important for the theoretical understanding of the economic growth and the demographic transition processes, and our results confirm the theory in Kalemli-Ozcan (2002) on the impact of endogenous child mortality change on fertility decline.

We also use our model to test the effect of female education on fertility rates. This is important for policymakers because a number of initiatives have been undertaken to reduce poverty in Sub-Saharan Africa, India and so on by reducing fertility rates through investments in female education based on prior research ( Cochrane, 1979 ). However, Cleland (2000) suggests reductions in child mortality are more critical in reducing fertility rates. Our model shows that, up to first-order effects, female education is an important variable in reducing fertility rates. But when we account for the non-linearities in the system and higher-order effects, reducing child mortality is more important than improving female education for reducing fertility rate.

Such analyses show how our approach can be used to evaluate policy initiatives such as the Millennium Development Goals (MDGs) with quantitative specificity. For instance, our analysis supports the conclusion of Easterly (2009) , Vandemoortele (2009) and others that the MDGs were unfair to Sub-Saharan Africa. We show that this is due to the differences in development trajectories in these countries caused by the inherent non-linearity in child mortality decline with respect to GDP. We suggest that, instead of setting arbitrary development targets, our non-linear dynamic model can be used to set country-specific development targets in the future, providing more feasible and fairer goals, especially for the upcoming Sustainable Development Goals initiative.

The data are from the World Bank “World Development Indicators” dataset ( WDI, 2015 ). This contains data for over 200 countries for a period of more than 50 years. For the economic indicator, we use the GDP per capita (in constant 2005 dollars). We use the log GDP value and call the variable G in the analysis.

We use child mortality as the mortality indicator (denoted by C ). Child mortality refers to the number of children not surviving to age 5 per 1,000 live births and is a strong indicator of child health. The total fertility rate is the fertility measure (denoted by A ) and is defined as the average number of children a woman has in the course of her reproductive lifetime.

We define the educational indicator E to be the average years of schooling for the female population as collected in the Barro–Lee dataset ( Barro and Lee, 2010 ). Since the data are available only on a 5-yearly basis in that dataset, we use linear interpolation to obtain yearly data points.

The entire dataset is also available in the Palgrave Communications ’ Dataverse repository ( Ranganathan et al., 2015a ).

The changes in the variables are modelled endogenously so that the model specifies how changes in each of the state variables takes place as a function of the current state of the system. For the demographic transition, the state of the system is defined by the values of C, G and A and we model the time evolution of these variables. We estimate the model from cross-country data and write the estimating equations in terms of the variable values for a given country at a given time instant as:

where we assume ϵ C ( i ,  t ), ϵ G ( i ,  t ) and ϵ A ( i ,  t ) are i.i.d normally distributed and independent for different countries i and at different time instants t . The functions f C (.), f G (.), f A (.) are modelled using polynomial basis functions in the state variables C, G, A . We include first-order and quadratic terms in the variables and their inverses along with all possible two-variable and three-variable interaction terms in the variables and their inverses. For example, the full specification of f C is

Thus, there are 33 terms in the full model specification, and the objective of the model selection algorithm we now present is to find the most efficient submodel that fits the data well. We do this in two stages. First, we rank all models with a given number of terms based on their log-likelihood score so that M 1 , M 2 , M 3 , … are the best possible models that include only 1, 2, 3, … polynomial terms, respectively. The log-likelihood scores for these models are an increasing function of the number of terms in the model.

In the second stage, we select the best model among these preselected models using the Bayesian marginal likelihood score, similar to the Bayes factor. For this, we assume a uniform, non-informative prior on the parameter space, so that every possible model coefficient is weighted equally (conditioned on the corresponding term being included in the submodel). This penalizes more complex models with larger number of terms as the dimension of the parameter space increases with increasing number of terms (see Ranganathan et al., 2014 for a fuller description of the approach).

We perform an additional test to find the best explanatory variable for each model. For instance, for the Δ C model, we test among all submodels that contain only C and one of the other two variables to test if two variables are sufficient to explain the Δ C data instead of all three. If we find that the Δ C data is explained well with only C and G variables and their interaction terms, we say that G explains changes in C adequately and is the variable with the most explanatory power for the Δ C model.

Robustness tests

We assumed the errors are independent for different countries and different time instants. However, performing independent estimations for the three variables is suboptimal if the error terms across the variables are correlated for the same countries at the same time instants (as may happen if there are systematic reasons for changes in the variable due to omitted variables, for example). We use a generalized least squares approach called the seemingly unrelated regressions ( Amemiya, 1985 ) to handle this case. This involves an iterative procedure where Ordinary Least Squares (OLS) estimates of the model coefficicients are first computed and the error covariance matrix is estimated based on this first model estimate. This error covariace matrix is then used to recompute the model coefficients and this two-step procedure is iterated until convergence.

Another issue related to model robustness is to test how the model performs on different subsamples of the data. We have fitted the data for all countries to obtain our models. Researchers have shown that development patterns may differ vastly in countries with different socio-economic conditions (for example, Masanjala and Papageorgiou, 2008 ; Crespo Cuaresma, 2011 ). So we expect that applying our method to specific groups of countries, such as only low-income countries or those in Sub-Saharan Africa, should give significantly different models from the overall model we look at here. But using non-random subsamples to test for robustness restricts our modelling to only a particular region of the phase space, which is not consistent with our goal of identifying the overall trend in the data.

We instead test for robustness using random subsamples with different fractions of the data used for training the model (50%, 60%, 70%, 80% and 95% of the full sample) and with 100 different iterations for each case. Estimates of model fit for each of these models are obtained on the remaining out-of-sample test data. If our models are robust, they will be chosen as the best in most of the iterations for different subsamples. As more of the data are used for training, the probability of the training subsample being representative of the full data increases but the probability of the out-of-sample data being representative of the full data simultaneously decreases. As we use the out-of-sample data for evaluating model fitting error, other models are selected more often than for smaller training fractions due to unrepresentative test sets. However robust models should still be chosen more frequently than these other models. Hence, we report two numbers for each given size of training dataset—the absolute frequency with which our model is chosen as the best model for the different subsamples, and the relative position of our model in the list of models selected for different subsamples.

Multicollinearity is an issue when using a large number of regressors that are related to each other. It is possible that some terms are correlated with each other and this results in less efficient models being accepted. In evaluating models based on the Bayes factor, there is an implicit penalty to increasing the number of terms indefinitely but it is useful to perform direct tests to detect multicollinearity. Durlauf et al. (2008) suggest methods from within the Bayesian framework but we look at a standard diagnostic test—the condition numbers or condition indices defined as the ratios of the individual singular values to the largest singular value in the singular value decomposition of X T X , where X is the design matrix ( Belsley et al., 1980 ). Condition numbers of over 50 (or 30 for conservative estimates) are considered to indicate presence of significant multicollinearity that may affect the OLS estimates.

Adding other explanatory variables

Our methodology expresses changes in the three variables only as a function of these three variables. However, it is well known that other variables, while not being part of the system in terms of the demographic transition, are important predictors of changes in these variables. For instance, education affects GDP growth, and has been postulated to cause fertility decline ( Barro, 1991 ) and child mortality decline ( Galor, 2005 ). Omitting these variables limits the explanatory power of our models.

However, these additional variables can be added in a straightforward manner to the model specification. If we wish to include the education variable into the full model for fertility decline, we can modify equation (3) so that we have

Similarly, if we wish to add more explanatory variables V 1 , V 2 , … that are known to be good predictors of Δ A , but we are interested only in the linear effect of V j on Δ A , we modify the equation as

where α j are the regression coefficients. This straightforward extension allows us to refine our models easily to get better fits by the addition of more explanatory variables.

Lagged effects

In socio-economic systems, indicator variables may have lagged effects on one another. To model these effects from within our framework, we find the Bayes factor of the best models with a lagged variable instead of the actual variable. For example, to investigate the possible lag effect for G in the Δ C model, we consider the modified estimating equation

for different values of the lag parameter τ and find the model that best fits the data using the methodology described above, while also evaluating the best lag parameter value.

For practical purposes, in this article, we modify this proposed approach slightly so that we first evaluate the best model using the methodology described above for the unlagged variables. For this best model, we investigate lag effects by evaluating the models for different values of the lag parameters. The first approach is more consistent with the Bayesian framework we have described earlier, but datasets with lagged variables are more sparse and the models that we obtain using the first approach may not be robust enough for lag analysis. Hence, we use the second approach to analyse lagged effects.

We apply the methods to the dataset with child mortality, log GDP per capita and fertility rate and find that the best dynamic model for the three key indicator variables ( C, G and A ) is given by

On the basis of Bayes factor values, we find that fertility rate is less important than GDP as a predictor of changes in child mortality. Similarly, to explain changes in fertility rate, the Bayes factor for models with only two variables C and A is relatively close to that of the models where all three variables are used. In the case of GDP, the two variable A and G model has a higher Bayes factor than the three variable model, which includes C . But alternative models for GDP also have similar Bayes factor values and hence it is not clear that this is the best possible Δ G model based on the data.

The interaction effects between the variables can be represented as shown in Fig. 1 . The overall cycle illustrated here is that child mortality decreases faster with higher GDP, fertility rate decreases faster when child mortality is low and decreases in fertility rate are faster at higher levels of GDP. In going through the cycle, we can see that there is a tendency of countries to go from the regime of high mortality, high fertility and low prosperity to a regime of low mortality, low fertility and high prosperity as described in the demographic transition literature.

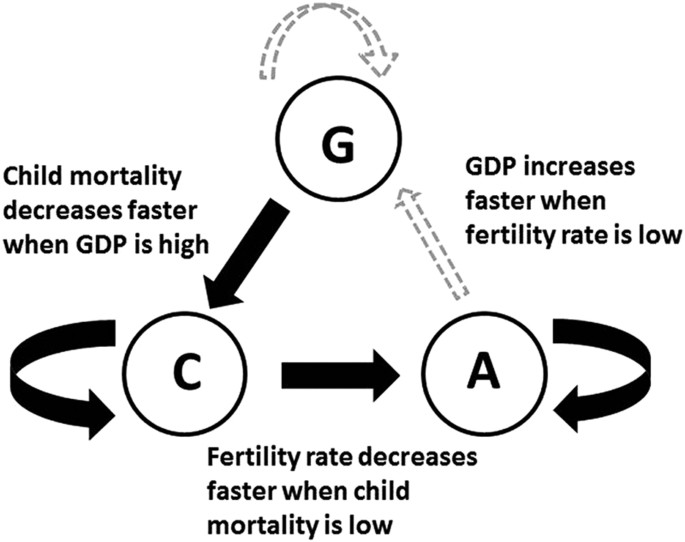
The Development Cycle as seen in the data for the three indicator variables. GDP drives changes in child mortality, which drives changes in fertility rate, which in turn drives changes in GDP. The arrow widths indicate the confidence in the model. The Δ C and Δ A models have much higher R 2 values than the Δ G model.

In addition to pointing to the basic structure of interactions, the models above also show the non-linearities involved. For example, the Δ C model summarizes a number of important facts about how child mortality has changed across different countries over the last 50 years. Child mortality declines non-linearly with C and G , and the mean proportional decrease per year is given by −Δ C / C =0.0028(1.6 G −0.02 C ). Percentage decrease in child mortality is therefore larger when GDP is high and when child mortality is low. Interestingly, without the second-order effect (the C 2 term in the equation (4)), this mechanism is similar to the equation for endogenous change in mortality assumed in Kalemli-Ozcan (2002) . Equation (4) shows a clear tendency to move towards low levels of child mortality, with a stable equilibrium point (that is, point where Δ C =0) at C *=0. There is a secondary effect that indicates that child mortality decreases more slowly with insufficient investment in child health. For instance, for two countries with the same G value but different C values, the country with the higher child mortality will experience a slower proportional decrease.

Similarly, we see that the fertility rate decreases faster when A is high, but this decrease is slowed if C is also high. There is also a secondary effect, which slows the percentage decrease in the fertility rate when A is low. The model shown above has two non-trivial equilibrium points (at roughly A *=10 and A *=1.5) obtained by solving the equation Δ A =0. The steady-state value A *=10 would correspond to a country with relatively low G and high C , and corresponds to the high mortality, high fertility and low economic growth regime in the demographic transition. The steady-state value A *=1.5 corresponds to a low mortality, low fertility and high economic growth regime. Thus, the two steady states correspond to the two opposite ends of the spectrum described in the demographic transition literature.

In the Δ G model, a high fertility rate slows economic growth. Solving Δ G =0 gives two equilibrium points, G *=4.4 and G *=11.6, suggesting that there is a slowdown in growth at both low and high GDP. We interpret the steady-state value of G *=4.4 as evidence of a transitory “poverty trap” ( Ranganathan et al., 2015b ), where countries are forced by certain self-reinforcing mechanisms to be trapped in a state of poverty without escape except through external means ( Bowles et al., 2006 ). The other steady state G *=11.6 indicates a slowing of economic growth in rich countries.

To evaluate the validity of the OLS estimates, we first test if the different error terms for different variables in the model are uncorrelated. We find there is only limited correlation (the maximum off-diagonal term in the scaled covariance matrix is 12% of the diagonal term). Hence, we are justified in assuming that the errors across variables are almost uncorrelated and we use the models obtained using this assumption. Performing generalized least squares using the seemingly unrelated regressions approach does not significantly alter the coefficients of the different terms and the iterative procedure converges quickly.

When we perform random subsample robustness tests on the models with 100 different subsamples, we find that the models specified by equations (4)–(6), are chosen a significant proportion of the time (69%, 45%, 96%, respectively, for the Δ C , Δ G , Δ A models) when 50% of the data are used for training. These numbers are necessarily lower (28%, 12% and 17%, respectively) when 95% of the data are used for training, as each test set is now very specific. However, our overall models remain the best models in terms of relative frequency. The Δ G and Δ A models in equations (5) and (6) are chosen more often than any other model for any fraction of training data used, while the Δ C model in equation (4) is chosen as the best model most often for all fractions of training data except for 95%, when it is chosen second most often. These results cumulatively support the conclusion that the models selected using our methodology are robust.

Next, we test if multicollinearity is a significant issue affecting the OLS estimates. Using the condition number test, we find that the Δ C model predictors CG and C 2 are not significantly correlated (condition numbers={1, 4.76}). For the Δ A model, we find slight evidence of multicollinearity (condition numbers={1, 3.3, 7.5, 35.67}) slightly above the conservative threshold of 30 but still below 50. For the Δ G model there is significant multicollinearity (condition numbers={1, 10.45, 246.8}). But as we noted earlier, a number of alternative models fit the Δ G data closely. In fact, while the other two models have R 2 values of 0.29 and 0.26, the Δ G model has a very low R 2 value of less than 0.01 suggesting a very weak relationship.

Additional variables: the effect of education on fertility

There are a number of important covariates to be considered when looking at changes in fertility rates ( Barro, 1991 ). Many policymakers work with female education as an important tool to reduce fertility rate and increase economic growth ( Cochrane, 1979 ; UN, 2002 ). International organizations such as the United Nations Population Fund and the World Bank advocate better schooling for girls as a means of achieving lower child mortality and fertility rate. However,the evidence is not conclusive as significant fertility declines have occurred without noticeable changes in female education ( Cleland, 2000 ; Basu, 2002 ). To test the hypothesis on whether female education is significant for fertility decline, we construct a model relating it to total fertility and test it against a model that relates child mortality to fertility.

We test the Δ A models containing only the two variables A and C in equation (6) against Δ A models containing only A and E . If C is a more significant predictor than E of Δ A , then those models will have higher Bayes factors. Figure 2 shows that education is the best single explanatory variable when only first-order effects are considered. For models that contain 2, 3 and 4 polynomial terms, models with C are better than models with E as the explanatory variable. If we go on to compute Bayes factor values for Δ A models with all these three variables ( A, E and C ) we find that the best 2, 3 and 4 term models involve only A and C . We conclude based on this that while higher female educational attainment does predict first-order decreases in fertility rate well, child mortality is the more effective predictor overall.

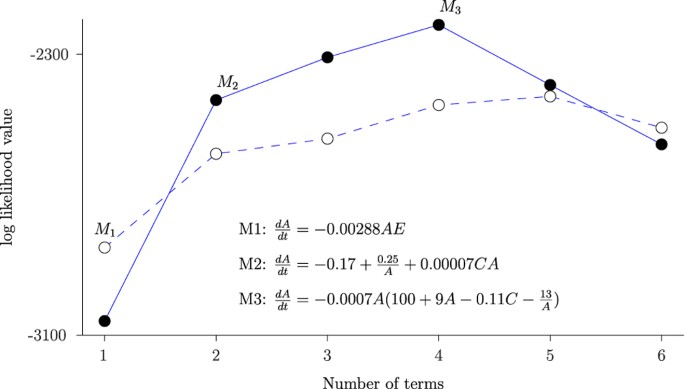
The log-Bayes factor plots for A-C models (solid circles) and A-E models (hollow circles), showing that child mortality is more important than average years of schooling as an explanatory variable for fertility rate. But for the simplest one-term models, the education indicator seems more crucial.

This explains empirical findings ( Cleland, 2000 ; Basu, 2002 )—while investments in female education are valuable, improvement in child health and investments in health-care systems in general might be more important.

We find the lagged effect of G on Δ C by evaluating the set of models

for values of τ ranging between −15 and 15 years and find that the rate of decrease in child mortality depends on the level of GDP in the preceding 5 years. There is no lagged effect of C on changes in C .

We repeat the same procedure for the Δ A model

now with C ( t − τ ) as the lagged variable. The results suggest that the longer lead we use on child mortality the better prediction we get on fertility rate decrease. This suggests that women use their future prediction of the probability of their child surviving when making fertility choice decisions. The greater the probability of future survival, the lower the fertility rate (this is again in agreement with the mechanism in the Kalemli-Ozcan, 2002 model). Finally, the Δ G model does not show significant improvement when using a lagged variable.

Some caution is required in the interpretation of these results. The dataset for lagged variables is necessarily shorter than that used in the original non-lagged fitting. Given the significant amount of missing data for poorer countries, the long lags might be a selection effect for richer countries where this data are available. As larger datasets become available for developing countries, these results should become clearer ( Fig. 3 ).

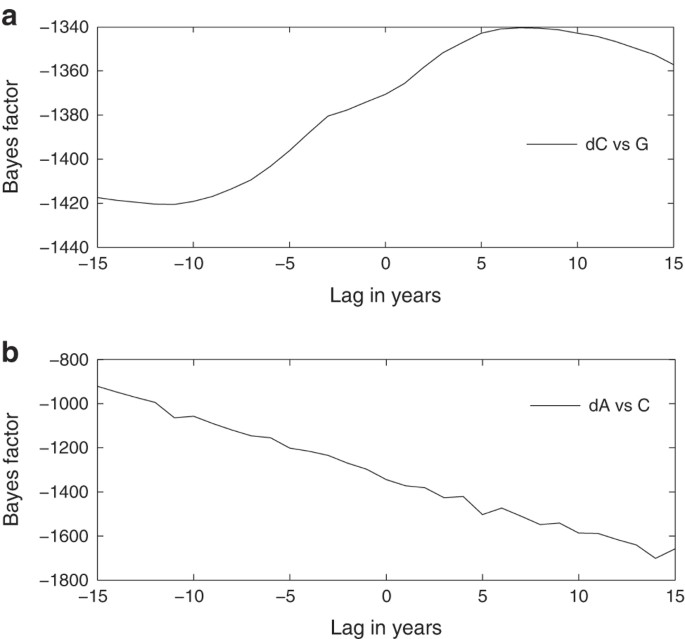
The log-Bayes factor plots for the Δ C and Δ A models as a function of the lag in G and C , respectively. (The Bayes factor values are reported in the log scale). The Δ C model suggests that a lag time of around 5 years in G is the best parameter for the Δ C models. A long lead time is suggested for C in the Δ A model.

We have constructed a model of the demographic transition and its relationship to economic growth using the key indicator variables log GDP per capita, child mortality and total fertility rate. Our important substantive findings relate to the sequence of events in the demographic transition and may be seen as a test of the theory proposed by Kalemli-Ozcan (2002 , 2003) . Child mortality is reduced as a result of economic growth with a possible lagged effect. The reduction in child mortality, or possibly anticipation of this change, then drives fertility rates down. Although a predictor of fertility, female education plays a less important role than child mortality. Finally, economic growth is mostly independent of the other indicators, but is weakly driven by lowered fertility. The link back to child mortality completes the development cycle.

The innovation of the approach we have presented here lies in identifying the dynamic interactions that best explain the demographic transition and its effects on economic growth. Our approach provides (1) an emphasis on yearly changes instead of long-run equilibria that may not be attained; (2) the modelling of non-linearities and interaction effects, which is the norm in most realistic complex systems; and (3) a robust model that best explains empirical evidence on the demographic transition. An important question is how we interpret our results in terms of causal mechanisms. Can we use the equations we have derived to understand the actions of people living in the countries from which data were collected? To address this question we now give an interpretation of the models we have obtained in the context of earlier theoretical literature.

Various causative mechanisms are proposed for the onset of the demographic transition. For instance, Becker (1981) and a large body of literature following his work explains the demographic transition as a consequence of increased investments in human capital due to economic growth or technological progress. Increased returns on education are also thought to initiate the demographic transition and therefore a decline in fertility ( Galor and Weil, 1999 ).

Our analysis and the cycle presented in Fig. 1 supports the models developed by Kalemli-Ozcan (2002 , 2003) and emphasizes endogenously lowered child mortality over increased economic opportunities as the more immediate cause of drops in fertility rates. From an individual mother’s point of view, if the probability of children surviving is lower, then having more children increases biological fitness. While GDP has some effect on changes in fertility rate, the best single predictor of decreases in fertility rate is child mortality. Economic growth, however, comes into the picture indirectly as high GDP increases the survival probability, probably as a result of improvements in economic and social conditions.

Similarly, we find that while female education does predict decreases in fertility, child mortality remains a better predictor of these decreases. The decision whether or not to have a child may well involve a trade-off against other economic and education opportunities ( Becker et al., 1990 ), but it is changes in the overall costs (and not just economic cost) of child bearing and child rearing that have the greatest role in decreasing fertility.

Although the emphasis on child mortality in the development cycle in Fig. 1 is different from that emphasized in some of the earlier work, the change in focus is relatively small. Importantly, none of our findings shift us a long way from those hypotheses previously proposed about human development. Instead, our analysis sharpens the picture by finding those models that are closest to all the available aggregate data. By fitting rate of change of indicators to their current state we have looked explicitly at how the state of the world in one year leads to the state of the world the following year.

This allows us to make robust short-term predictions on the evolution of the state of the system as defined by the three variables. There has been strong criticism of the MDGs ( Easterly, 2009 ; Vandemoortele, 2009 ) for setting arbitrary development targets. As our methodology models changes in the child mortality, we can integrate it forward simultaneously with the other variables to make quantitative predictions on future values of child mortality for each specific country (as we have done in Ranganathan et al., 2015b ). With this expected future value as a baseline value and a desired policy improvement based quantitatively on deviations from the business-as-usual scenario (say one standard deviation better than business-as-usual value), a feasible but fair development target can be set for each country.

From an econometric standpoint, in modelling the demographic transition, we have omitted many covariates specific to each indicator variable and hence do not explain the processes fully. For instance, adult mortality is an important variable and Kalemli-Ozcan (2002) and Soares (2005) include it in their models of fertility choice. The long lead time in our lagged effects analysis of the fertility rate model (equation (7)) suggests the importance of considering adult mortality. Child mortality levels are correlated with adult mortality levels and the inclusion of future child mortality levels in our model could be a proxy for women using future adult mortality levels in making decisions based on whether their children will survive into adulthood. Similarly, the growth econometrics literature has discussed in detail the important covariates of economic growth and these need to be included in our models to explain changes in log GDP ( Barro, 1991 ; Durlauf et al., 2008 ; Ley and Steel, 2009 ).

However, our approach captures the interactions between the key variables and can be extended in a straightforward manner (as discussed in the Methods section) to include other variables of interest. We can add these additional variables either as control variables with only linear effects on the change variable or into the full framework of our methodology with non-linear and interaction effects. This will directly contribute to improving model fit and our understanding of the particular processes. Endogeneity is an important consideration when adding more explanatory variables. We show that our models are reasonably robust to the data but the addition of new variables may make the statistical estimates inefficient and this needs to be considered carefully.

From the statistical methods standpoint, we use non-informative priors on the parameter and the model space because we use an exploratory approach to obtain the model that best explains the data. To define “best fit”, we assumed that any submodel (equivalent to specifying the set of non-zero coefficients in the full model) is equally likely and that any model coefficient has an equal prior probability of being present. This is equivalent to assuming a discrete uniform prior on the model space ( George, 2010 ). Chipman (1996) suggests the use of heredity priors to ensure that interaction terms are likely to be present only in models where the main effects are present. When we test our models with the strong heredity priors suggested by Chipman (1996) , we find models with different terms. However, we prefer the uniform prior on the model space because some mechanisms can be better represented by using higher-order interaction terms without main effects. For instance, the Δ C model in equation (4) includes interaction and non-linear effects and no main effects, and hence would not be selected if a strong heredity prior were used. But the model we find suggests a mechanism whereby proportional changes (Δ C / C ) as opposed to absolute changes (Δ C ) are linearly related to the main effects C and G .

Finally, from the mechanistic standpoint, the approach we have taken in this article can be contrasted with one that starts from the point of view of underlying micro-level interactions of economic agents. There are a number of limitations to the micro-level modelling approach, with respect to providing succinct and empirically accurate models of data. First, although based on observations, such models do not necessarily provide the best fit to the existing data as they do not test alternative models. Instead, correlational evidence is provided for particular assumptions or predictions. The advantage of the Bayes factor-based analyses we have performed here is that they provide a likelihood measure over a number of plausible models. A second limitation of micro-level economic models is that they usually involve specific mathematical forms that limit the range of models, which can be studied formally using the available tools. While these restrictions help mathematical analysis, they are not necessarily feasible in terms of mechanisms and restrict the degree to which non-linearities in the data can be captured by the model. A third limitation is that, despite their mathematical tractability, the statement of such models is often not amenable to direct policy applications in comparison with a set of equations such as equations (4)–(6), which can be used to predict short-term evolutions in the state variables robustly.

At the same time, while the approach we have outlined in this article avoids these limitations, we use no underlying assumptions and thus provide no a priori causal basis for our models. This criticism must be taken seriously because, without identifying underlying mechanisms, there are always a multitude of possible models. But letting the data reveal the patterns helps us discuss, in a post-analysis stage as we have done above, how the derived models relate to the micro-level motives of economic actors.

Data Availability

The datasets analysed are available in Palgrave Communications ’ Dataverse repository ( Ranganathan et al., 2015a ): http://dx.doi.org/10.7910/DVN/1ZUDJI . These datasets are from the World Bank World Development Indicators dataset and the Barro–Lee dataset.

Additional Information

How to cite this article: Ranganathan S, Swain RB, Sumpter DJT (2015) The demographic transition and economic growth: implications for development policy. Palgrave Communications . 1:15033 doi: 10.1057/palcomms.2015.33.

Amemiya T (1985) Advanced Econometrics . Blackwell: Oxford.

Google Scholar  

Barro RJ (1991) Economic growth in a cross-section of countries. The Quarterly Journal of Economics ; 106 (2): 407–443.

Barro RJ and Becker GS (1989) Fertility choice in a model of economic growth. Econometrica ; 57 (2): 481–501.

Barro RJ and Lee J-W (2010) A new data set of educational attainment in the world, 1950–2010. Working Paper 15902, National Bureau of Economic Research, http://www.nber.org/papers/w15902 .

Basu AM (2002) Why does education lead to lower fertility? A critical review of some of the possibilities. World Development 30 (10): 1779–1790.

Becker GS (1981) A Treatise on the Family . Harvard University Press: Cambridge, MA.

Becker GS, Murphy KM and Tamura R (1990) Human capital, fertility, and economic growth. Journal of Political Economy 98 (5), S12–S37.

Belsley DA, Kuh E and Welsch RE (1980) Regression Diagnostics: Identifying Influential Data and Sources of Collinearity . John Wiley & Sons: New York, USA.

Ben-Porath Y (1976) Fertility Response to Child Mortality: Micro Data from Israel . M. Falk Institute for Economic Research: Israel.

Bowles S, Durlauf SN and Hoff K (2006) Poverty Traps . Princeton University Press: Princeton, New Jersey.

Brock W, Durlauf SN and West KD (2007) Model uncertainty and policy evaluation: Some theory and empirics. Journal of Econometrics ; 136 (2): 629–664.

Chipman H (1996) Bayesian variable selection with related predictors. The Canadian Journal of Statistics/La Revue Canadienne de Statistique ; 4 (1): 17–36.

Cigno A (1998) Fertility decisions when infant survival is endogenous. Journal of Population Economics ; 11 (1): 21–28.

CAS   Google Scholar  

Cleland JG (2000) The Effects of Improved Survival on Fertility: A Reassessment . Population Council: New York, pp 60–92.

Cochrane SH (1979) Fertility and Education: What Do We Really Know? Johns Hopkins University Press: Baltimore, MD.

Crespo Cuaresma J (2011) How different is Africa? A comment on Masanjala and Papageorgiou. Journal of Applied Econometrics ; 26 (6): 1041–1047.

Cutler DM, Deaton AS and Lleras-Muney A (2006) The determinants of mortality. NBER Working Paper 11963, Cambridge, MA.

Durlauf SN, Johnson PA, Temple JR (2005) Growth econometrics In: Aghion P and Durlauf SN (eds) Handbook of Economic Growth ; Vol. 1. Elsevier: Amsterdam, pp 555–677.

Durlauf SN, Kourtellos A and Tan CM (2008) Are any growth theories robust? The Economic Journal ; 118 (527): 329–346.

Easterly W (2009) How the Millennium Development Goals are unfair to Africa. World Development ; 37 (1): 26–35.

Eckstein Z, Mira P and Wolpin KI (1999) A quantitative analysis of Swedish fertility dynamics: 1751–1990. Review of Economic Dynamics 2 (1): 137–165.

Fernandez C, Ley E and Steel MF (2001) Model uncertainty in cross-country growth regressions. Journal of Applied Econometrics ; 16 (5): 563–576.

Filmer D and Pritchett L (1999) The impact of public spending on health: Does money matter? Social Science & Medicine ; 49 (10): 1309–1323.

Galor O (2005) The transition from stagnation to growth: Unified growth theory In: Aghion P and Durlauf SN (eds) Handbook of Economic Growth . Elsevier: Amsterdam.

Galor O and Moav O (2002) Natural selection and the origin of economic growth. The Quarterly Journal of Economics 117 (4): 1133–1191.

Galor O and Weil DN (1996) The gender gap, fertility, and growth. The American Economic Review ; 86 (3): 374–387.

Galor O and Weil DN (1999) From Malthusian stagnation to modern growth. The American Economic Review ; 89 (2): 150–154.

George EI (2010) Dilution priors: Compensating for model space redundancy. In: Berger JO, Cai TT and Johnstone IM (eds). Borrowing Strength: Theory Powering Applications-A Festschrift for Lawrence D. Brown . Institute of Mathematical Statistics: Beachwood, Ohio, USA, pp 158–165.

Haines MR (1998) The relationship between infant and child mortality and fertility: Some historical and contemporary evidence for the United States. In: Montgomery MR and Cohen B (eds). From Death to Birth: Mortality Decline and Reproductive Change . National Academy Press: Washington DC, pp 227–253.

Heckman JJ and Walker JR (1990) The relationship between wages and income and the timing and spacing of births: Evidence from Swedish longitudinal data. Econometrica ; 58 (6): 1411–1441.

Kalemli-Ozcan S (2002) Does the mortality decline promote economic growth. Journal of Economic Growth ; 7 (4): 411–439.

Kalemli-Ozcan S (2003) A stochastic model of mortality, fertility, and human capital investment. Journal of Development Economics ; 70 (1): 103–118.

Kögel T and Prskawetz A (2001) Agricultural productivity growth and escape from the Malthusian trap. Journal of Economic Growth ; 6 (4): 337–357.

Ley E and Steel MF (2009) On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. Journal of Applied Econometrics ; 24 (4): 651–674.

Masanjala WH and Papageorgiou C (2008) Rough and lonely road to prosperity: A reexamination of the sources of growth in Africa using Bayesian model averaging. Journal of Applied Econometrics ; 23 (5): 671–682.

Rajkumar AS and Swaroop V (2008) Public spending and outcomes: Does governance matter? Journal of Development Economics ; 86 (1): 96–111.

Ranganathan S, Swain RB and Sumpter DJT (2015a) The demographic transition and economic growth: Implications for development policy. Dataverse. http://dx.doi.org/10.7910/DVN/1ZUDJI , accessed 16 September 2015.

Ranganathan S, Nicolis SC, Spaiser V and Sumpter DJ (2015b) Understanding democracy and development traps using a data-driven approach. Big Data ; 3 (1): 22–33.

Ranganathan S, Spaiser V, Mann RP and Sumpter DJ (2014) Bayesian dynamical systems modelling in the social sciences. PloS One ; 9 (1): e86468.

Rutstein S and Medica V (1978) The Latin American experience. In: Preston SH (ed). The Effects of Child and Infant Mortality on Fertility ; Academic Press, New York, USA, pp. 93–112.

Sah RK (1991) The effects of child mortality changes on fertility choice and parental welfare. Journal of Political Economy ; 99 (3): 582–606.

Sala-i Martin X (1997) I just ran four million regressions. NBER Working Paper 6252, Cambridge, MA.

Soares RR (2005) Mortality reductions, educational attainment, and fertility choice. American Economic Review ; 95 (3): 580–601.

Strulik H (2004) Economic growth and stagnation with endogenous health and fertility. Journal of Population Economics ; 17 (3): 433–453.

Tamura R (1996) From decay to growth: A demographic transition to economic growth. Journal of Economic Dynamics and Control 20 (6–7): 1237–1261.

Tamura R (2002) Human capital and the switch from agriculture to industry. Journal of Economic Dynamics and Control ; 27 (2): 207–242.

UN. (2002) Completing the fertility transition. Population Bulletin of the UN Special Issues (48/49).

Vandemoortele J (2009) The MDG conundrum: Meeting the targets without missing the point. Development Policy Review ; 27 (4): 355–371.

WDI. (2015) World Development Indicators 2015. The World Bank, http://elibrary.worldbank.org/doi/abs/10.1596/978-1-4648-0440-3 , accessed 16 September 2015.

Wolpin KI (1997) Determinants and consequences of the mortality and health of infants and children. In: Rosenzweig MR and Stark O (eds). Handbook of Population and Family Economics ; Elsevier: Amsterdam, pp 483–557.

Download references

Acknowledgements

This work was funded by ERC grant 1DC-AB and Swedish Research Council grant D049040.

Author information

Authors and affiliations.

Department of Mathematics, Uppsala University, Uppsala, Sweden

Shyam Ranganathan & David JT Sumpter

Stockholm School of Economics & Södertörn University, Stockholm, Sweden

Ranjula Bali Swain

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Shyam Ranganathan .

Ethics declarations

Competing interests.

The authors declare no competing financial interests.

Rights and permissions

This work is licensed under a Creative Commons Attribution 3.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/

Reprints and permissions

About this article

Cite this article.

Ranganathan, S., Swain, R. & Sumpter, D. The demographic transition and economic growth: implications for development policy. Palgrave Commun 1 , 15033 (2015). https://doi.org/10.1057/palcomms.2015.33

Download citation

Received : 26 May 2015

Accepted : 17 September 2015

Published : 03 November 2015

DOI : https://doi.org/10.1057/palcomms.2015.33

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Climate and land-use changes drive biodiversity turnover in arthropod assemblages over 150 years.

• Silvio Marta
• Michele Brunetti
• Gentile Francesco Ficetola

Nature Ecology & Evolution (2021)

Economic growth and population transition in China and India 1990–2018

• Aalok Ranjan Chaurasia

China Population and Development Studies (2021)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Philos Trans R Soc Lond B Biol Sci
• v.364(1532); 2009 Oct 27

Human population growth and the demographic transition

The world and most regions and countries are experiencing unprecedentedly rapid demographic change. The most obvious example of this change is the huge expansion of human numbers: four billion have been added since 1950. Projections for the next half century expect a highly divergent world, with stagnation or potential decline in parts of the developed world and continued rapid growth in the least developed regions. Other demographic processes are also undergoing extraordinary change: women's fertility has dropped rapidly and life expectancy has risen to new highs. Past trends in fertility and mortality have led to very young populations in high fertility countries in the developing world and to increasingly older populations in the developed world. Contemporary societies are now at very different stages of their demographic transitions. This paper summarizes key trends in population size, fertility and mortality, and age structures during these transitions. The focus is on the century from 1950 to 2050, which covers the period of most rapid global demographic transformation.

1. Introduction

After centuries of very slow and uneven growth, the world population reached one billion in 1800. The modern expansion of human numbers started then, rising at a slow but more steady pace over the next 150 years to 2.5 billion in 1950. During the second half of the twentieth century, however, growth rates accelerated to historically unprecedented levels. As a result, world population more than doubled to 6.5 billion in 2005 (United Nations 1962 , 1973 , 2007 ). This population expansion is expected to continue for several more decades before peaking near 10 billion later in the twenty-first century. Around 2070, the world's population will be 10 times larger than in 1800.

The recent period of very rapid demographic change in most countries around the world is characteristic of the central phases of a secular process called the demographic transition . Over the course of this transition, declines in birth rates followed by declines in death rates bring about an era of rapid population growth. This transition usually accompanies the development process that transforms an agricultural society into an industrial one. Before the transition's onset, population growth (which equals the difference between the birth and death rate in the absence of migration) is near zero as high death rates more or less offset the high birth rates typical of agrarian societies before the industrial revolution. Population growth is again near zero after the completion of the transition as birth and death rates both reach low levels in the most developed societies. During the intervening transition period, rapid demographic change occurs, characterized by two distinct phases. During the first phase, the population growth rate rises as the death rate declines while the birth rate remains high. In the second phase, the growth rate declines (but remains positive) due to a decline in the birth rate. The entire transition typically takes more than a century to complete and ends with a much larger population size.

The plot of world population size over time in figure 1 (top solid line) shows the typical S-shaped pattern of estimated and projected population size over the course of the transition. Population growth accelerated for most of the twentieth century reaching the transition's midpoint in the 1980s and has recently begun to decelerate slightly. Today, we are still on the steepest part of this growth curve with additions to world population exceeding 75 million per year between 1971 and 2016.

Population size estimates, 1900–2005 and projections 2005–2050. High, medium and low variants.

Contemporary societies are at very different stages of their demographic transitions. Key trends in population size, fertility and mortality during these transitions are summarized below. The focus is on the century from 1950 to 2050, covering the period of most rapid global demographic change. The main source of data is the United Nation's 2006 world population assessment, which provides estimates for 1950–2005 and projections from 2005 to 2050 ( United Nations 2007 ).

2. Future population trends

The projected rise in world population to 9.2 billion in 2050 represents an increase of 2.7 billion over the 2005 population of 6.5 billion. Nearly all of this future growth will occur in the ‘South’—i.e. Africa, Asia (excluding Japan, Australia and New Zealand), and Latin America—where population size is projected to increase from 5.3 to 7.9 billion between 2005 and 2050 ( table 1 ). In contrast, in the ‘North’ (Europe, Northern America, Japan and Australia/New Zealand), population size is forecast to remain virtually stable, growing slightly from 1.22 to 1.25 billion between 2005 and 2050. The difference in trends between these two world regions reflects the later stage of the transition in the North compared with the South.

Table 1.

Population estimates (1950–2005) and projections (2005–2050), by region. Adapted from United Nations (2007) .

The global demographic transition began in the nineteenth century in the now economically developed parts of the world (the North) with declines in death rates. Large reductions in birth rates followed in the early part of the twentieth century. These transitions are now more or less complete. But, as shown in table 1 , trends for the two principal regions in the North are expected to diverge between 2005 and 2050: an increase from 0.33 to 0.45 billion in Northern America, and a decline from 0.73 to 0.66 billion in Europe. In fact, several countries in Europe (e.g. Russia) and East Asia (e.g. Japan) face significant population declines as birth rates have fallen below death rates.

The demographic transitions in Africa, Asia and Latin America started later and are still underway. In 2005, Asia had a population of 3.94 billion, more than half of the world total, and its population is expected to grow by 34 per cent to 5.27 billion by 2050. Africa, with 0.92 billion inhabitants in 2005, is likely to experience by far the most rapid relative expansion, more than doubling to 2.0 billion by 2050. Latin America, with 0.56 billion in 2005, is the smallest of the regions of the South; its projected growth trend is similar to that of Asia.

It may seem surprising that population growth continues at a rapid pace in sub-Saharan Africa, where the AIDS epidemic is most severe. This epidemic has indeed caused many deaths, but population growth continues because the epidemic is no longer expanding and the birth rate is expected to remain higher than the elevated death rate in the future ( UNAIDS 2007 ; Bongaarts et al . 2008 ). The epidemic's demographic impact can be assessed by comparing the standard UN population projection (which includes the epidemic's effect) with a separate hypothetical projection in which AIDS mortality is excluded ( United Nations 2007 ). In sub-Saharan Africa, the former projects a 2050 population of 1.76 billion and the latter a population of 1.95 billion. The difference of 0.2 billion in 2050 between these projections with and without the epidemic is due to deaths from AIDS as well as the absence of the descendents from people who died from AIDS. According to these projections, the population of sub-Saharan Africa will grow by one billion between 2005 and 2050 despite the substantial impact of the AIDS epidemic. In fact, no country is expected to see a decline in its population size between 2005 and 2050 due to high AIDS mortality. Most populations in sub-Saharan Africa will more than double in size, several will triple and Niger is expected to quadruple by 2050 ( United Nations 2007 ).

Transitions in the developing world have generally produced more rapid population growth rates in mid-transition than historically observed in the North. In some developing countries (e.g. Kenya and Uganda), peak growth rates approached four per cent per year in recent decades (implying a doubling of population size in two decades), levels that were very rarely observed in developed countries except with massive immigration. Two factors account for this very rapid expansion of population in these still largely traditional societies: the spread of medical technology (e.g. immunization, antibiotics) after World War II, which led to extremely rapid declines in death rates, and a lag in declines in birth rates.

Population sizes for the 10 largest countries in 2005 and in 2050 are presented in table 2 . In 2005, China (1.31 billion) and India (1.13 billion) were by far the largest countries, together accounting for nearly half the South's total. The top 10 include six Asian countries and only one country each in Latin America and Africa. By 2050, the ranking is expected to have shifted substantially, with India's population exceeding China's, and with Ethiopia and DR Congo rising to the top 10, replacing Japan and the Russian Federation.

Table 2.

Ten largest countries by population size in 1995 (estimate) and 2050 (medium projection). Adapted from United Nations (2007) .

To simplify the presentation of results, all projections discussed in this study are taken from the medium variant of the UN projections ( United Nations 2007 ). The UN has a good record of making relatively accurate projections ( National Research Council 2000 ), but the future is of course uncertain and actual population trends over the next half century will likely diverge to some extent from current projections. The UN makes an effort to capture this uncertainty by publishing separate high and low projections. For the world, the high and low variants reach 7.8 and 10.8 billion, respectively, in 2050, indicating a rather wide range of possible outcomes (see dashed lines in figure 1 ).

3. Drivers of population growth: fertility and mortality

The world's population increases every year because the global birth rate exceeds the death rate. For example, in 2000–2005 population size increased at a rate of 1.17 per cent per year, which equals the difference between a birth rate of 2.03 per cent and a death rate of 0.86 per cent. At the country level, population growth is also affected by migration, but for the regional aggregates of population used in this analysis, migration is usually a minor factor, and it will therefore not be discussed in detail.

The annual birth and death rates of populations are in turn primarily determined by levels of fertility and mortality experienced by individuals. The most widely used fertility indicator is the total fertility rate (TFR), which equals the number of births a woman would have by the end of her reproductive years if she experienced the age-specific fertility rates prevailing in a given year. Mortality is often measured by the life expectancy (LE) at birth, which equals the average number of years a newborn would live if subjected to age-specific mortality rates observed in a given year.

(a) Fertility

The UN's past estimates and future projections of fertility levels by region for the period 1950–2050 are presented in figure 2 . In the 1950s, the TFR in the South was high and virtually stable at around six births per woman on average. This high level of fertility reflects a near absence of birth control, a condition that has prevailed for centuries before the middle of the twentieth century. In the late 1960s, a rapid decline in fertility started nearly simultaneously in Asia and Latin America. In contrast, Africa has experienced only limited reproductive change. As a result of these divergent past trends, fertility levels in 2000–2005 differed widely among regions from as high as 5 births per woman (bpw) in Africa, to 2.5 bpw in Asia and Latin America. Average fertility in the North was already low in the early 1950s and has since declined to 2.0 bpw in Northern America and to 1.4 bpw in Europe.

Trends in the total fertility rate by region.

The decline in the average fertility in the South from 6 to 3 bpw over the past half century has been very rapid by historical standards. This reproductive revolution is mainly due to two factors. First, desired family size of parents has declined as the cost of children rose and child survival increased. Second, government intervention played a key role. In China this took the form of a coercive and unpopular one-child policy, but most other countries implemented voluntary family planning programmes. The aim of these programmes is to provide information about and access to contraceptives at subsidized prices so that women who want to limit their childbearing can more readily do so.

UN projections for the South assume that the TFR will eventually reach and then fall slightly below the so-called ‘replacement’ level in all regions. Replacement fertility is just above 2 bpw and it represents the level at which each generation just replaces the previous one, thus leading to zero population growth (in the absence of mortality change and migration). Below-replacement fertility produces, in the long run, population decline. As is evident from figure 2 , the TFRs in Asia and Latin America are expected to reach the replacement level around 2020. Africa is assumed to be on a much slower trajectory towards replacement fertility because of its lower level of socio-economic development. High fertility therefore remains a key cause of future population growth in this region. In contrast, the already low fertility of the North is expected to remain below replacement and is no longer driving population growth.

(b) Mortality and life expectancy

Mortality levels have also changed rapidly over the past several decades ( figure 3 ). The South experienced exceptional improvements in LE from an average of 41 years in 1950–1955 to 64 years in 2000–2005. By the early 2000, Latin America reached mortality levels similar to those prevailing in the North in the 1970s, and Asia was just a few years behind. Africa experienced the highest mortality and improvements in LE stalled in the 1990s due to the AIDS epidemic. As a result, Africa's LE, at 52 years in 2000–2005, was still substantially below that of Asia (68) and Latin America (72). As expected, Europe and Northern America already achieved relatively low levels of mortality by 1950, but they have nevertheless seen significant further improvements since then. Europe's LE (74) is now lower than North America's (78) because of a rise in mortality in Eastern Europe after the break-up of the Soviet Union.

Trends in LE by region.

Projections of future LEs by the UN assume continued improvements over time in all regions. The North is expected to reach 82 years in 2050 despite the increasing difficulty in achieving increments as countries reach ever higher levels of LE. Asia and Latin America are expected to continue to close the gap with the North, and Africa will continue to lag, in part because the continent remains affected by the AIDS epidemic.

It should be noted that the assumptions made by the UN about future trends in fertility and mortality are not based on a firm theoretical basis. Instead, the UN relies on empirical regularities in past trends in countries that have completed their transitions, mostly in the North, where fertility declined to approximately the replacement level, and increases in LE became smaller over time. This is a plausible approach that unfortunately leaves room for potential inaccuracies in projection results.

4. Changing population age composition

Over the course of the demographic transition, declines in fertility and mortality cause important changes in a population's age composition. In general, countries in the early stages of the transition have a younger age structure than countries in the later stages.

Figure 4 presents the distribution of the 2005 population in four broad age groups: 0–14, 15–24, 25–64 and 65+ by region. Most of the regions in the South—Africa, Latin America, South Asia and West Asia—have very young age structures with about half of the population under age 25 (62% in Africa). The exception is East Asia (mostly China) where this proportion is 37 per cent. In the North, the population under 25 is still smaller: 35 per cent in North America and just 30 per cent in Europe. The reverse pattern is observed for the proportion 65+, which is much higher in the North than in the South, ranging from as high as 15 per cent in Europe to as low as just 3 per cent in Africa.

Distribution of population by age, by region, 2005.

(a) The age-dependency ratio

A changing age distribution has significant social and economic consequences, e.g. for the allocation of education, healthcare and social security resources to the young and old. Assessments of this impact often rely on the so-called age-dependency ratio (DR) that summarizes key changes in the age structure. The DR at a given point in time equals the ratio of population aged below 15 and over 65 to the population of age 15–64. This ratio aims to measure how many ‘dependents’ there are for each person in the ‘productive’ age group. Obviously, not every person below 15 and over 65 is a dependent and not every person between ages 15 and 65 is productive. Despite its crudeness, this indicator is widely used to document broad trends in the age composition.

Over the course of a demographic transition, the DR shows a characteristic pattern of change. Figure 5 presents this pattern as observed in the South from 1950 to 2005 and projected from 2005 to 2050. Early in the transition, the DR typically first rises slightly as improvements in survival chances of children raise the number of young people. Next, the DR falls sharply as declines in fertility reduce the proportion of the population under age 15. This decline has important economic consequences because it creates a so-called ‘demographic dividend’, which boosts economic growth by increasing the size of the labour force relative to dependents and by stimulating savings ( Birdsall et al . 2001 ). Finally, at the end of the transition, the DR increases again as the proportion of the population over age 65 rises. Figure 5 also plots the DR of the North from 1950–2050. From 1950 to 2010 it showed a slight decline, but after 2010 it rises steeply as very low fertility and increasing longevity increases the proportion 65+. This ageing of the North poses serious challenges to support systems for the elderly (OECD 1998 , 2001 ).

Dependency ratio estimates, 1950–2005.

(b) Population momentum

At the end of the demographic transition natural population growth reaches zero once three conditions are met:

• Fertility levels-off at the replacement level of about 2.1 bpw (more precisely, the net reproduction rate should be 1). If fertility remains above replacement, population growth continues.
• Mortality stops declining. In practice, this is not likely to happen because improvements in medical technology and healthcare as well as changes in lifestyles, etc. will probably ensure continued increases in LE.
• The age structure has adjusted to the post-transitional levels of fertility and mortality.

The adjustment of the age structure at the end of the transition takes many decades to complete. A key implication of this slow adjustment process is that population growth continues for many years after replacement fertility is reached if, as is often the case, the population is still relatively young when fertility reaches the replacement level. The tendency of population size to increase after a two-child family size has been reached is referred to as population momentum ; it is the consequence of a young population age structure (‘young’ is defined relative to the age structure in the current life table) ( Bongaarts & Bulatao 1999 ).

The population momentum inherent in the age structure of a particular population at a given point in time can be estimated with a hypothetical population projection in which future fertility is set instantly to the replacement level, mortality is held constant and migration is set to zero. Since such a variant is not directly available from UN projections, it will not be presented here. However, the UN does provide ‘instant replacement’ projections in which mortality and migration trends are the same as in the standard projection. This projection gives an approximation of the combined effect on future growth of population momentum and declining mortality in the South because the role of migration is small. The difference between this hypothetical projection and the standard medium UN projection is a measure of the impact of high fertility on future population growth.

Results of these two projections are presented in figure 6 , which compares the per cent growth between 2005 and 2050 for regions in the South. The black bars give the growth in the standard (medium variant) projection and the grey bars give the growth in the ‘instant replacement’ projection. Three results are noteworthy. First, the two projections differ most in Africa (+117% versus +50%) which is as expected because fertility is still very high in this region. Second, in all regions of the South outside China, populations would be expected to rise by 50 per cent (62% in West Asia) if fertility were set to replacement in 2005. This implies that momentum and declining mortality are responsible for nearly half of the projected future population growth in Africa and for the large majority of growth in Latin America, and South and West Asia. Third, in East Asia and in Latin America the replacement projection exceeds the medium UN projection. This finding is explained by the fact that fertility in these regions is assumed to average below the replacement level over the next half century.

Percentage increase in population 2005–2050, by region, alternative projections. Black bars denote medium UN projection; grey bars denote instant replacement projection (hypothetical).

5. Conclusion

The world and most countries are going through a period of unprecedentedly rapid demographic change. The most obvious example of this change is the huge expansion of human numbers: four billion have been added since 1950. Other demographic processes are also experiencing extraordinary change: women are having fewer births and LEs have risen to new highs. Past trends in fertility and/or mortality have led to very young populations in high fertility countries in the South and to increasingly older populations in the North. Still other important demographic changes which were not reviewed here include rapid urbanization, international migration, and changes in family and household structure.

Global population growth will continue for decades, reaching around 9.2 billion in 2050 and peaking still higher later in the century. The demographic drivers of this growth are high fertility in parts of the South, as well as declining mortality and momentum. This large expansion in human numbers and of the accompanying changes in the age structure will have multiple consequences for society, the economy and the environment as discussed in the subsequent chapters in this issue.

One contribution of 14 to a Theme Issue ‘ The impact of population growth on tomorrow's world ’.

• Birdsall N., Kelley A., Sinding S.2001 Population matters: demographic change, economic growth and poverty in the developing world Oxford, UK: Oxford University Press [ Google Scholar ]
• Bongaarts J., Bulatao R.1999 Completing the demographic transition . Popul. Dev. Rev. 25 , 515–529 ( doi:10.1111/j.1728-4457.1999.00515.x ) [ Google Scholar ]
• Bongaarts J., Buettner J., Heilig G., Pelletier F.2008 Has the AIDS epidemic peaked? Popul. Dev. Rev. 34 , 199–224 ( doi:10.1111/j.1728-4457.2008.00217.x ) [ Google Scholar ]
• National Research Council 2000 Beyond six billion: forecasting the world's population (eds Bongaarts J., Bulatao R.). Washington, DC: National Academy Press [ Google Scholar ]
• OECD 1998 Maintaining prosperity in an ageing society Paris: OECD Publications [ Google Scholar ]
• OECD 2001 The fiscal implications of ageing: projections of age-related spending . OECD Economic Outlook 69 , 145–167 [ Google Scholar ]
• UNAIDS 2007 AIDS Epidemic Update Geneva: UNAIDS [ Google Scholar ]
• United Nations 1962 Demographic yearbook New York, NY: United Nations [ Google Scholar ]
• United Nations 1973 The determinants and consequences of population trends New York, NY: Department of Economic and Social Affairs, Population Studies 50, United Nations [ Google Scholar ]
• United Nations 2007 World population prospects: the 2006 revision New York, NY: United Nations Population Division [ Google Scholar ]

This website uses cookies.

By clicking the "Accept" button or continuing to browse our site, you agree to first-party and session-only cookies being stored on your device to enhance site navigation and analyze site performance and traffic. For more information on our use of cookies, please see our Privacy Policy .

• Journal of Economic Perspectives

The Demographic Transition: Three Centuries of Fundamental Change

• Article Information
• Comments ( 0 )

JEL Classification

• O15 Economic Development: Human Resources; Human Development; Income Distribution; Migration

You are using an outdated browser. Please upgrade your browser to improve your experience.

• Publications
• IZA Discussion Papers
• The Demographic Transition: Causes and Consequences

January 2012

IZA DP No. 6334: The Demographic Transition: Causes and Consequences

published in: Cliometrica, 6(1), 1-28

This paper develops the theoretical foundations and the testable implications of the various mechanisms that have been proposed as possible triggers for the demographic transition. Moreover, it examines the empirical validity of each of the theories and their significance for the understanding of the transition from stagnation to growth. The analysis suggests that the rise in the demand for human capital in the process of development was the main trigger for the decline in fertility and the transition to modern growth.

• demographic transition
• human capital
• Unified Growth Theory

Cookie settings

These necessary cookies are required to activate the core functionality of the website. An opt-out from these technologies is not available.

In order to further improve our offer and our website, we collect anonymous data for statistics and analyses. With the help of these cookies we can, for example, determine the number of visitors and the effect of certain pages on our website and optimize our content.

Human Capital and Economic Opportunity Global Working Group

Demographic transitions across time and space.

The demographic transition—the move from a high fertility/high mortality regime into a low fertility/low mortality regime—is one of the most fundamental transformations that countries undertake. To study demographic transitions across time and space, we compile a data set of birth and death rates for 186 countries spanning more than 250 years. We document that (i) a demographic transition has been completed or is ongoing in nearly every country; (ii) the speed of transition has increased over time; and (iii) having more neighbors that have started the transition is associated with a higher probability of a country beginning its own transition. To account for these observations, we build a quantitative model in which parents choose child quantity and educational quality. Countries differ in geographic location, and improved production and medical technologies diffuse outward from Great Britain, the technological leader. Our framework replicates well the timing and increasing speed of transitions. It also produces a strong correlation between the speeds of fertility transition and increases in schooling similar to the one in the data.

• Tools and Resources
• Customer Services
• Behavioral Science and Health Education
• Biostatistics and Data
• Disaster Preparation and Response
• Environmental Health
• Epidemiology
• Global Health
• Health Services Administration/Management
• Infectious Diseases
• Non-communicable Diseases
• Public Health Policy and Governance
• Public Health Profession
• Sexual and Reproductive Health
• Special Populations
• Theory and Methods
• Share This Facebook LinkedIn Twitter

Article contents

Demographic transition in india: insights into population growth, composition, and its major drivers.

• Usha Ram Usha Ram International Institute for Population Sciences, Department of Public Health and Mortality Studies
•  and  Faujdar Ram Faujdar Ram Population Council of India and International Institute for Population Sciences
• https://doi.org/10.1093/acrefore/9780190632366.013.223
• Published online: 26 April 2021

Globally, countries have followed demographic transition theory and transitioned from high levels of fertility and mortality to lower levels. These changes have resulted in the improved health and well-being of people in the form of extended longevity and considerable improvements in survival at all ages, specifically among children and through lower fertility, which empowers women. India, the second most populous country after China, covers 2.4% of the global surface area and holds 18% of the world’s population. The United Nations 2019 medium variant population estimates revealed that India would surpass China in the year 2030 and would maintain the first rank after 2030. The population of India would peak at 1.65 billion in 2061 and would begin to decline thereafter and reach 1.44 billion in the year 2100. Thus, India’s experience will pose significant challenges for the global community, which has expressed its concern about India’s rising population size and persistent higher fertility and mortality levels. India is a country of wide socioeconomic and demographic diversity across its states. The four large states of Uttar Pradesh, Bihar, Madhya Pradesh, and Rajasthan accounted for 37% of the country’s total population in 2011 and continue to exhibit above replacement fertility (that is, the total fertility rate, TFR, of greater than 2.1 children per woman) and higher mortality levels and thus have great potential for future population growth. For example, nationally, the life expectancy at birth in India is below 70 years (lagging by more than 3 years when compared to the world average), but the states of Uttar Pradesh and Rajasthan have an average life expectancy of around 65–66 years.

The spatial distribution of India’s population would have a more significant influence on its future political and economic scenario. The population growth rate in Kerala may turn negative around 2036, in Andhra Pradesh (including the newly created state of Telangana) around 2041, and in Karnataka and Tamil Nadu around 2046. Conversely, Uttar Pradesh, Bihar, Madhya Pradesh, and Rajasthan would have 764 million people in 2061 (45% of the national total) by the time India’s population reaches around 1.65 billion. Nationally, the total fertility rate declined from about 6.5 in early 1960 to 2.3 children per woman in 2016, a result of the massive efforts to improve comprehensive maternal and child health programs and nationwide implementation of the national health mission with a greater focus on social determinants of health. However, childhood mortality rates continue to be unacceptably high in Uttar Pradesh, Bihar, Rajasthan, and Madhya Pradesh (for every 1,000 live births, 43 to 55 children die in these states before celebrating their 5th birthday). Intertwined programmatic interventions that focus on female education and child survival are essential to yield desired fertility and mortality in several states that have experienced higher levels. These changes would be crucial for India to stabilize its population before reaching 1.65 billion. India’s demographic journey through the path of the classical demographic transition suggests that India is very close to achieving replacement fertility.

• demographic transition
• contraception
• family planning
• life expectancy
• child mortality

India is one of the oldest civilizations and has a vibrant cultural heritage coupled with remarkable diversity. The Mughals ruled the country from 1526 to 1761 , and were mainly located north of Vindhyanchal. India was a British colony from 1612 until 1947 , when the country attained its independence and became a sovereign nation. The British occupied all of present-day India after defeating Tipu Sultan in Mysuru and Marathas in Maharashtra. The British East India Company governed India and controlled trade throughout the region, except for Goa, which the Portuguese controlled in 1510–1961 , and Pondicherry, which the French controlled in 1673–1693 and again in 1699–1962 .

India has conducted a regular decadal census since 1881 that measures population size and composition as well as decadal growth at the national and subnational levels (including states, districts, and tehsils). At the dawn of Indian independence, there were about 345 million Indians. The year 1951 witnessed the first census of an independent India, recording a total population of 361 million and a moderate annual exponential growth rate of 1.25% during 1941–1951 . From a population growth perspective, the year 1951 became a turning point because it indicated a population explosion since it multiplied threefold by 2001 .

According to a United Nations (UN, 2019 ) report, India constituted 17.7% of the total world population, and was second only to China, whose share was 18.5%. The same estimates revealed that India would not only surpass China in the year 2030 with its share of 17.6% (and China’s would decrease to 17.1%) but it would also maintain the first rank after 2030 . The report further indicated that Africa’s share would rise to 25.6% in 2050 and 39.4% in 2100 . In contrast, the percentage share of Asia would decline from 59.5% in 2020 to 43.4% in 2100 . By 2100 , India would attain the first rank as far as the share of a single country is concerned. Nonetheless, its relative share would decline to 16.8% in 2050 and 13.3% in 2100 . It is thus essential to examine the dynamics of population growth, its potential, and future drivers of population growth of India.

The rapid population growth caused by a comparatively quick decline in mortality and persisting higher fertility levels has been the cause of concern in most developing counties, including India. The 1961 census of India revealed an annual exponential national growth rate close to 2% during 1951–1961 . The concerns were raised about the population growth and its rising size, both nationally and globally. The demographics of India—population size, growth rate, fertility, mortality, and so on—continue to occupy significant space discussions concerning its impact on various global health and developmental indicators. Alarmed at burgeoning numbers, and a view to accelerating a rapid decline in fertility levels, many developing countries, especially in Southeast Asia, launched official family planning programs in the mid-1960s. In the 1970s and 1980s, most witnessed a strong commitment by leaders to reduce fertility levels. As a result, they experienced one of the fastest transitions in levels of fertility (Pathak & Ram, 1981 ; Srinivasan & Pathak, 1981 ). Although India launched an official family planning program in the early 1950s, the real inputs for the program were recorded from the 1960s, when the program became method-mixed and target oriented. Post-independence, upon the advice of several researchers (Chitre, 1964 ; Gopalaswamy, 1962 ; Laxmi, 1964 ), the Indian government implemented its official family planning program in 1952 that promoted sterilization on a large scale. This was considered as the most cost-effective and impactful approach by the government given resource constraints. However, Agarwala ( 1964 ) disagreed with this and criticized the program. Recently, Srinivasan ( 2006 ) also opined that the continuous focus on sterilization (female) has dominated the Indian national family planning program. In the mid-1960s, government expanded the basket of methods for the clients and included IUD into the program. This, nonetheless failed due to several side effects on the users (Pujari et al., 1967 ).

The well-known linguistic, economic, and social-cultural diversity of India and its century-old demographic diversity across geographies have expanded, especially since independence. Several states in India, including Andhra Pradesh, Karnataka, Kerala, and Tamil Nadu in the southern region, have moved much faster in achieving the national goal of the replacement fertility. The onset of fertility transition in these southern states occurred when the social and development indicators such as female literacy rates, per capita income, mortality and so on were rather poorer. At the same time, Hindi-speaking states in the northern region, including Bihar, Madhya Pradesh, Rajasthan, and Uttar Pradesh, continue to experience high levels of fertility as well as mortality. Nationally, fertility levels in India have fallen, and by 2000 Indian women were having an average of about 3.3 children. A significant portion of this decline came from the states in the southern region, where female literacy rates were higher, and women enjoyed greater autonomy than the women in the rest of India. While the southern states of Kerala and Tamil Nadu attained replacement-level fertility long ago, the giant northern states of Uttar Pradesh, Bihar, Madhya Pradesh, and Rajasthan continue to reproduce at a prodigious rate (Krishnamoorthy, 1997 ; Rajan, 1994 ; Seal & Talwar, 1994 ). It is important to note that the prevailing social and economic conditions in the southern states at the time of onset of fertility transitions varied considerably. The doctrine of demographic-transition theory advocates indicates that a rise in per capita income, industrialization, and urbanization subsequently leads to reduced levels of fertility and mortality in populations. However, this did not happen in Kerala. Fertility and mortality levels in Kerala were not accompanied by the concurrent improvements in the levels of per capita income, industrialization, and urbanization (Zachariah, 1983 ).

Until the end of the 20th century , family welfare programs and policies in India focused on lowering fertility rates because the authorities visualized that the persisting higher fertility rates would further add to the built-in growth momentum of its population age composition. The UN’s ( 1987 ) population projections revealed that the population momentum alone would add substantially to growing numbers in India. Visaria and Visaria ( 1994 ) warned that the ultimate population size of India would be enormous if the country failed to put a brake on the fertility rate and achieved the replacement levels before 2016 . It would thus be useful to elaborate on the demographic transition in India and identify gaps to provide future directions for the program to enable positive changes in matters of population growth, thereby improving the lives and well-being of its people. The national scenario masks the diversity across states. Thus, achieving the goals may be less feasible without any understanding of the issues at the subnational level. This article documents the demographic transition of India at the national and subnational levels and examines various drivers of the transition.

The data for the present research come from several sources. The world population for the past and future years comes from the UN’s ( 2019 ) World Population Prospects . The time-series data for India on population size, growth rates, and age distribution at the national and state levels come from Indian government censuses conducted between 1881 and 2011 . The Government of India’s National Commission on Population (NCP, 2019 ) projections provides the numbers for the period 2021–2036 . The indicators of fertility (total fertility rates) and mortality (infant mortality rate, under-5 mortality rate, and life expectancy at birth come) are from various rounds of the Indian government’s Sample Registration System (SRS). The data for multiple years is available in the annual statistical reports published by the Registrar General of India ( 2020 ). The information on contraceptive use and marriage comes from the National Family Health Surveys (International Institute for Population Sciences [IIPS], 1993 ; IIPS & ICF, 2017 ; IIPS & ORC-Macro, 2000 , 2007 ). Figures and tables presented throughout the article give detailed data from these sources.

Demographic Transition Theory: A Brief Description

The demographers Warren Thompson ( 1929 ) and Adolphe Landry circa 1934 (Landry, 1987 ), described the classical demography/population transition. However, Frank W. Notestein ( 1945 ), an American demographer proposed a precise framework and presented a systematic formulation of the theory in its real sense According to the demographic transition theory, most countries will go through a process of population change from the stage of high birth and death rates (pretransition stage 1) to the last stage of lowest birth and death rates (stage 4). In other words, countries move from the lowest pretransition stage 1 (sometimes negative growth rate) to the highest growth rate (stages 2 and 3) before reaching stage 4, when the growth rate is extremely low (occasionally negative) and the country has attained below-replacement fertility. According to the theory, the demographic transition of a nation can be described with the help of the growth rates if the country has regular censuses over a reasonably long period. In his critical exploration of the demographic transition, Kirk ( 1996 ) stated that

the timing of the decline in countries with Non-European tradition conformed to the forecast by the original authors of the theory, without exception, fall in mortality preceded the decline in the levels of fertility . . . In general, the transition period was shorter in Non-European countries than the countries inhabited by Europeans. (p. 383)

Further, the non-European countries are transitioning with a lower level of socioeconomic development (Cleland & Wilson, 1987 ).

Several researchers (Kaa, 1987 , 2002 ; Lesthaeghe, 2011 , 2014 ; Lesthaeghe & Surkyn, 2004 ) have referred to a second demographic transition (SDT). The SDT is a period of continued fertility decline much below-replacement fertility. The most critical factors related to this continued decline are increase in nonmarriage, individual autonomy, self-actualization, rising symmetry in sex roles, advancing female education, and economic independence of women (for details, see Lesthaeghe, 2014 ). Nevertheless, the postulate of SDT based on the experiences of European countries may not hold in developing countries (Cleland, 2001 ; Dyson, 2010 ). The SDT, nevertheless, is much more challenging than the original demographic transition because the countries face declining population sizes, shrinking working population, and graying population. To an extent, replacement migration could help these nations overcome these emerging challenges. Coleman ( 2006 ), using the emergence of migrants as the dominant community in some geographies compared to the natives, advocated the concept of the third demographic transition (TDT), which emphasizes the drastic change in population composition. However, the idea of TDT could be a reflection of the adjustment for the shrinking labor force that arises out of SDT, and it does not fit into the purview of demographic transition theory per se.

This section discusses changes in population size, growth and its age-sex composition over time to understand India’s population transition. This is followed by a detailed exploration of the crucial factors that led to population transition. For this, we have considered four major drivers of population change that include fertility, mortality, family planning and changes in marriage pattern. Changes in fertility levels have been studied using total fertility rate. The changes in mortality have been studied using three indicators of infant mortality, under-5 mortality and expectation of life at birth. The changes in contraceptive use is examined with the help of contraceptive prevalence rate. Finally, changes in marriage pattern is examined with the help of percentage of women aged 20–24 years who were married before reaching age 18 years and women aged 30–34 years who remained single.

Population Size, Growth, and Age Structure

The UN ( 2019 ) estimated a total of 7,795 million people globally in 2020 . They suggested that this number would surpass 10 billion by the turn of the 21st century (Table 1 ). In 2020 , about 60% of the people live in Asia and a little over 17% live in Africa. By 2100 , Asia would be home to 43% of the global people and Africa to 39%. The share of European countries is estimated to reduce from 9.6% in 2020 to less than 6% in 2100 . While a similar pattern is predicted for the countries in Latin America and the Caribbean and the North American regions, the share of Oceania remains unchanged. China’s population, was about 19% of the global population in 2020 , would reduce to less than 10% by 2100 . In India the share would decrease from less than 18% in 2020 to slightly over 13% in 2100 .

Table 1. Population Size and Share of the Population of World Regions, China, and India, 2020–2100

Source: UN ( 2019 ).

The indirect estimates of crude birth and death rates for India are for the period 1901–1961 . After 1971 , the SRS, which was established in the late 1960s, started to provide the crude birth rate (CBR) and crude death rate (CDR) for India and bigger states annually. The most recent SRS estimates are available for the year 2017 . At the beginning of the 20th century , India had very high levels of crude birth and death rates (48 births/deaths per 1,000 persons; Figure 1 ), which persisted until 2021 . The death rates started to decline around 1930 and reached 16 deaths per 1,000 persons in 1971 . The CBR, too, began to fall at a much slower pace. While the CBR was 36 births per 1,000 persons in the early 1970s, the CDR was 16 deaths per 1,000 persons. This declining trend continues, and the gap between the two rates is narrowing over time. The CBR was 20 per 1,000 persons in 2017 as compared to the CDR of 6 per 1,000 persons.

Figure 1. Crude birth rate (CBR) and crude death rate (CDR) for India, 1901–2017.

At the beginning of the 20th century , India had 238 million people. The results of the first census of the new millennium revealed that India had crossed the one billion mark by the end of the 20th century as the 2001 census enumerated a total of 1,029 million Indians (Table 2 ). The country annually added 16.1 million people in the 1980s and 18.2 million in the 1990s. While the world population increased threefold (from 2 to 6 billion) during the last century, it grew five times in India. The 15th census of India conducted in 2011 enumerated a total of 1,210 million Indians. The population of India grew with a decadal growth rate of about 17.5% during 2001–2011 , resulting in an annual exponential growth rate of 1.62% (a decline from 1.96% observed during 1991–2001 ). Despite a substantial reduction in the growth rate during 2001–2011 , India added nearly 181 million people. The UN’s 2019 projections indicated a similar addition during 2011–2021 , before the country experienced a drastic decline in the subsequent decades.

Figure 2. Estimated and observed exponential annual population growth rate (%) during 1901–2011 and 2021–2101, respectively, for India.

Indian annual population growth peaked at 2.22% during 1961–1971 (Table 1 and Figure 2 ) and stayed around 2% for the next four decades until 2001 . This period may be referred to as the second stage (population explosion stage) of demographic transition for India, during which the country added approximately 590 million people. Between 2001 and 2011 India experienced a substantial decline in its population growth rate (from 1.95% in 1991–2001 to 1.62% in 2001–2011 ). The UN’s 2019 assessment suggested that as far as the population size as concerned, India would surpass China in the next 7–8 years and would continue to increase until the year 2061 when its population size would reach 1,650 million. India may experience a decline in its total population after 2061 and count 1,444 million people in the year 2101 . Thus, India would add another 440 million people to its 2011 population size before achieving stabilization. In other words, India is likely to enter the fourth stage (near-zero growth rate) in the next 50 years or so. For India, the third stage of the demographic transition may fall between 2011 and 2051 . The momentum inbuilt in the age structure of the population would mostly lead to its growth.

Table 2. Population Size, Intercensal Change (Absolute and Percentage), and Exponential Annual Growth Rate, India, 1901–2001

Source : Registrar General of India ( n.d.-a ); Population estimated from UN ( 2019 ).

Examination of the current growth rate in specific states of India, especially for the larger Indian states (in terms of population size), helps to locate growth potentials. Table 3 gives population size for 2001 and 2011 , the two recent censuses of India, absolute change and state share in the total national change during 2001–2011 , and the exponential population growth rate observed during 2001–2011 for 20 large states of India. The four states of Uttar Pradesh, Bihar, Madhya Pradesh, and Rajasthan deserve particular attention. With a population increase of 33.6 million, Uttar Pradesh contributed the most significant growth to the total national change of 182.2 million during 2001–2011 , followed by Bihar at 21.1 million and Maharashtra at 15.5 million. Kerala recorded the lowest annual exponential growth rate of 0.48%, followed by Andhra Pradesh (1.04%), Punjab (1.30%), and Odisha (1.31%). Bihar, Madhya Pradesh, Rajasthan, and Uttar Pradesh together added 446 million (43%) of the total national addition and each state had an annual growth rate of 2% or more. These states are likely to make significant contributions to Indian population growth in the future because the fertility and mortality rates in these states are comparatively high and the decline in these rates has been much slower than that of other states. The most recent projections of the Government of India (NCP, 2019 ) indicated that by the year 2036 there would be a total of 596 million Indians, and half of them would come from these four states.

Table 3. Population Size, Intercensal Change (Absolute and Percentage), and Exponential Annual Growth Rate for Selected States of India, 2001–2011

a Sum of states may not match to India due to rounding of the numbers.

b Undivided including Telangana.

Table 4 gives a future population scenario in the 13 large states of India subdivided into three groups based on the attainment of the replacement level of fertility. These 13 states together cover nearly 80% of the national total. Group 1 consists of four states—Rajasthan, Uttar Pradesh, Bihar, and Madhya Pradesh—that have yet to attain replacement fertility. Group 2 and Group 3 consist of the states that have recently reached replacement fertility and a long time ago, respectively. The four large states in Group 1 have enormous potential for growth, and during 2026–2036 their combined growth rate is projected to be close to 1% (0.83%). Bihar is an outlier even within this group, with a growth rate of 1.16% annually. Group 2 states would have a growth rate of around 0.37% and Group 3 of about 0.20%. These findings indicate that a major part of India’s population growth potential lies in the four states of Group 1.

Table 4. Population Size and Year of the Attainment of Replacement Fertility in 13 Large States of India Stratified by Level of Total Fertility Rate, 2011–2036

a 2011 population data from the census of India.

b Projected population for the period 2016–2036 is from NCP ( 2019 ).

c Undivided including Uttarakhand.

d Undivided including Jharkhand.

e Undivided including Chattisgarh.

Source : NCP ( 2019 ).

Population Age-Sex Composition

The population age-sex composition of a country narrates historical experiences, including wars, epidemics, famines, and so on. Population age distribution and the female to male ratio are indicative of fertility and mortality levels and the social status of the women in the populations. Along with the demographic transition in India described earlier, there has been an inevitable change in the age-sex structure—that is, the decline in mortality followed by fertility has resulted in changes to the population’s age structure. Several studies have debated and discussed the role of these changes in economic growth. Sex composition (population sex ratio overall and, more important, at birth) reflects the status of women in the society. Globally, the population sex ratio (males per 1,000 females) is favorable to the female gender. An overall sex ratio of 1,030–1,050 females per 1,000 males is standard under the natural conditions. The situation is slightly different in India.

Table 5 gives the sex ratio overall and for children younger than 5 years of age for India for a period of 120 years ( 1881–2011 ) along with the absolute change in them. For India, the overall sex ratio was close to normal until around 1931 . It started to rise gradually in favor of males after that. The 1991 census of India revealed a higher overall sex ratio nationally: 1,078 males per 1,000 females. However, the scenario is different for the child sex ratio. Female children marginally outnumbered male children until 1941 as the sex ratio was in favor of the female children (960–995 male children per 1,000 female children below age 5). However, the scenario reversed when the 1951 census results were declared as the child sex ratio turned in favor of male children (1,008 male children per 1,000 female children) and has deepened over the years with the widening female-male children gap. The child sex ratio in India increased from 1,022 in 1981 to 1,047 in 1991 and further to 1,071 in 2001 and 1,082 in 2011 male children per 1,000 female children. Nationally, during the periods 1981–1991 and 1991–2001 , the child sex ratio increased astonishingly by 25 and 24 units, respectively. The distorted child sex ratio in India as well as in neighboring countries in the region has been a matter of concern and point of debate and investigations among policy makers and researchers. Many have cited widespread gender-based discrimination (neglect) in the form of son preference, lower autonomy to the women, and so on as the leading cause of this distortion. These practices result in sex-selective abortions and gender-specific mortality differentials (Bongaarts, 2013 ; Bongaarts & Guilmoto, 2015 ; Guilmoto et al., 2018 ; Jha et al., 2011 ; Kashyap, 2019 ; Ram & Ram, 2018 ).

Table 5. Sex Ratio (Males per 1,000 Females) of the Total Population and Children Younger Than 5 Years of Age, India, 1881–2011

Notes: The sex ratio for the years 1881 and 1891 was calculated using data from Mukherji ( 1976 ). The sex ratio for children younger than 5 years of age was calculated using data from a C-series in the respective census of India.

Source : Registrar General of India ( n.d.-b ).

A few studies have estimated a decrease in girls due to the practice of sex-selective abortions in India and found that these practices are not universal across geographies. Instead, they vary considerably in subregions of India (Jha et al., 2011 ; Ram & Ram, 2018 ). Table 6 presents the sex ratio for selected states in India for the period 1991–2011 and the change in it. Regardless of the year, Kerala is the only state that has an overall sex ratio lower than 1,000 (i.e., females exceeding the male population). In addition, the male-female gap has widened over the past two decades by almost 43 units. Punjab and Haryana have the most skewed overall sex ratio, varying between 1,117 and 1,162 males per 1,000 females. The overall sex ratio has been in favor of males in the remaining states. However, the gaps in sex ratio seemingly have bridged over time. While the decline was sharp in the states of Uttar Pradesh, West Bengal, and Assam, it has remained mostly similar in Madhya Pradesh and Maharashtra. Similar to the overall sex ratio, Haryana and Punjab had a highly skewed child sex ratio, varying between 1,128 and 1,144, respectively, in 1991 and 1,190 and 1,169 in 2011 . In 2011 , Gujarat (1,110), Rajasthan (1,120), and Maharashtra (1,117) also showed a child sex ratio skewed in favor of male children. Other states also showed a considerable deficit of female children. Haryana topped the list as the child sex ratio increased by 62 units in favor of males during 1991–2011 . The corresponding increase was by 59 units in Maharashtra, 50 units in Rajasthan, 44 units in Gujarat, 42 units in Madhya Pradesh, and 30–39 units in Andhra Pradesh, Bihar, Odisha, and Uttar Pradesh. Kerala was the only state where the child sex ratio improved in favor of female children by 16 units between the 1991 and 2011 censuses.

Table 6. Sex Ratio (Males per 1,000 Females) of the Total Population and Children Younger Than 5 Years of Age for India and Selected States, 1991–2011

Note: Sex ratio from respective censuses of India (Table C-6 of 1991 and C-14 of 2001 and 2011).

a Undivided including Telangana.

Almost half of the districts in the country in 2011 had a deficit of girl children. The practice of neglect of the female child resulting in sex-selective abortion and excess female mortality is universal (Guilmoto et al., 2018 ; Ram & Ram, 2018 ). A more recent analysis for India by Kashyap ( 2019 ) indicated the dominance of prenatal factors (sex-selective abortion) compared to excess female mortality (postnatal factor). Table 7 presents the sex ratio at birth (SRB) for India and selected states. The data suggest that the SRB is favorable to male children for India nationally and subnationally. Punjab and Haryana, followed by Rajasthan, Uttar Pradesh, Gujarat, and Bihar, had a highly disturbing SRB in 1999 . For every 100 female births, Punjab and Haryana recorded 125 to 126 male births each, the other states recorded 112 to 118 male births. The male-female imbalance at birth has continued over time, although with a sign toward bridging the gaps. At the national level, the SRB has mostly remained unchanged at 112 male children for every 100 female children. Nonetheless, the imbalance has widened in Andhra Pradesh, Assam, and Haryana, suggesting that the efforts to address this have failed to yield desirable results. The study by Jha et al. ( 2011 ) demonstrated that the practices are more prevalent among affluent and educated people.

Table 7. Sex Ratio at Birth (Male Births Per 1,000 Female Births) and Absolute Change in Sex Ratio at Birth in India and Selected States, 1999–2016

a Undivided including Telangana for the years 1999, 2004, 2009, and 2013.

b Undivided including Jharkhand for the year 1999.

c Undivided including Chhattisgarh for the year 1999.

d Undivided including Uttarakhand for the years 1999, 2004, and 2009.

Source: Sex ratio from the annual statistical report of the Sample Registration System of India.

Table 8 presents age distribution by sex and dependency ratios (child, old age, and overall) for the period 1981–2011 (census of India) and 2036 for India (NCP, 2019 ). Figures 3A and 3B present age-sex population pyramids. The results in Table 8 suggest a visible change in the age structure over the decades. Nationally, the share of children below age 15 in the total population declined to from about 40% in 1981 to 31% in 2011 . The NCP ( 2019 ) projections indicated that the share would decrease to 20% by 2036 . The percentage of people aged 60 years and older increased to 9% in 2011 and is estimated to reach 15% in 2036 (over 227 million). The changes in the dependency ratios for children and older people also confirm a transition in the age structure. While the child dependency ratio in India declined from 73% in 1981 and to 51% in 2011 , the dependency ratio for older people increased marginally from 12% to 14%. The official population projections suggest that in 2036 the child dependency ratio would further decline to 30% and the dependency ratio for older people would increase to 23% nationally. In 2001 , India had about 587 million people in the working ages, between 15 and 59 years. Those aged 15–34 years accounted for nearly 60% (349 million). The number of people in the working ages of 15–59 years and 15–34 years increased to 733 million and 425 million, respectively, in the year 2011 . Population projections suggest that in 2036 , while the number of people of working age would increase to almost 989 million, young labor would reach 464 million. Such changes would impact future economic development and would call on the government to initiate innovative strategies to take care of the older population. Besides, a sharp rise in the labor force demands generation of more employment.

Table 8. Share of the Male and Female Population Out of the Total Population by Age Groups and Dependency Ratios (for Children, Older People, and Overall), India, 1981–2011 and 2036

a Population is taken from the censuses of India 1981, 1991, 2001, and 2011.

b Projected population for 2036 is from NCP ( 2019 ).

c Dependency ratio from author calculations. The child dependency ratio is defined as the number of children below 15 years of age per 100 persons in the working ages of 15–59 years. The old-age dependency ratio is defined as the number of persons aged 60 years or older per 100 persons in the working ages of 15–59 years. The overall dependency ratio is defined as the number of children below 15 years of age and persons aged 60 years or older per 100 persons in the working ages of 15–59 years.

Figure 3A. Age-sex population pyramids of India, 1991.

Figure 3B. Age-sex population pyramids of India, 2036.

Major Drivers of Population Growth

Three drivers impact the population growth rate and are responsible for demographic transition: fertility, mortality, and international migration. Generally speaking, international migration has a limited role, as its volume is small. Thus, it is mainly the changes in fertility and mortality levels in a population that lead to demographic transition. This section discusses fertility and mortality transition in India and specific programmatic interventions responsible for the change in the fertility and mortality levels. India lacks good quality civil registration data on births and deaths (Ram et al., 2020 ; Yadav & Ram, 2019 ). Until the early 1970s, the estimated fertility and mortality for India and its states came from indirect methods that used census data stratified by age and sex. In the early 1970s, the Registrar General of India launched an annual nationwide system of collecting data on fertility and mortality (known as the sample registration system; SRS), which provides invaluable data for India and its states, especially for the bigger states. For the most part, the present research used fertility and mortality data from the SRS.

Figure 4 presents the total fertility rate (TFR) for India spanning over nearly 150 years (Ram et al., 1995 ). The TFR gives the number of children a woman would have at the end of the reproductive period, assuming that she experiences the prevailing age patterns of fertility. The data suggests that the TFR in India virtually remained unchanged at around 6.3 children per woman from 1871–1881 until 1951–1961 (standard deviation = 0.27). There has been little fluctuation in the TFR, which is mainly attributed to the variations in the quality of age-sex data in different censuses (Mukherji, 1976 ). Coale’s ( 1986 ) proposition of survival strategy postulates that a TFR of less than six for the expectation of life at birth (e o o ) of 20–25 years could lead to a zero or negative population growth. Thus, under a high mortality regime, maintaining a TFR of 6 and above was an excellent strategy to ensure moderate positive population growth. The decline in the TFR during the period 1896–1901 might have been the result of the famines of 1896–1997 and 1899–1901 , which were among the worst ever experienced in history and affected substantial sections of the population (Dyson, 1991 ).

The fertility transition in India most likely began during the late 1960s. Since the inception of fertility transition, the TFR in India declined by 19% to about 1.1 fewer children per woman during the first decade ( 1966–1971 to 1976–1981 ). The 1960s witnessed a substantial change in the family planning program in India, which became target-oriented and included the introduction of intrauterine devices to the official program in 1965 . The initial inherent demand for family planning and a persistently higher level of fertility may have been the reason for a relatively faster fertility decline during the first decade following the onset of the demographic transition. In the next decade ( 1976–1981 to 1986–1991 ), although the decrease in fertility continued, its pace slowed down. The decline in TFR slowed down notably in the subsequent decade of 1976–1981 to 1986–1991 when the reduction was only about 15%. The coercive approach adopted during the emergency period ( 1975–1977 ) was mainly responsible for this reduction in several states, more specifically in the larger Hindi-speaking states of Bihar, Madhya Pradesh, Rajasthan, and Uttar Pradesh. This in turn accelerated the decline in TFR. Between 1986–1991 and 1996–2001 , the TFR declined by 19% (from about 4 children to 3.2 children per woman). During 1996–2001 , the TFR in India declined by about 14%. The mid-1990s saw a paradigm shift in the national family planning program as the country revamped the program from a target-oriented to target-free regime. This paradigm shift resulted in an initial decline/stagnation in the family planning performance in the country.

Figure 4. Total fertility rate, India, 1871–2018.

Nationally, the TFR almost halved in the 30 years between 1986 and 2016 from 4.2 to 2.3 children per woman (Table 9 ). Many states in India showed a similar trend. Rural India also experienced a decline in the TFR from 4.5 in 1986 to 2.5 in 2016 . However, urban India had already achieved replacement fertility in 2006 . Of the states included in this analysis, eight states have already attained replacement or below-replacement fertility. The lagging states are Bihar Madhya Pradesh, Rajasthan, and Uttar Pradesh, where TFR continues to be close to 3 children per woman. As noted, these are the states that are or could be center for India population growth in the coming years. The urban areas in several states attained replacement or below-replacement fertility in 2016 : the urban areas had a TFR of as low as 1.3 children per woman in West Bengal, 1.4 in Odisha, 1.5 in Andhra Pradesh, and 1.6 in Karnataka and Tamil Nadu. Further, the rural areas of Andhra Pradesh, Karnataka, Kerala, Maharashtra, Punjab, Tamil Nadu, and West Bengal had a TFR that varied between 1.7 and 1.9 children per woman in 2016 .

Table 9. Total Fertility Rate for Combined, Rural, and Urban Areas and the Ratio of Rural to Urban Rate for India and Selected States, 1986–2016

a Undivided including Telangana for the years 1986, 1996, and 2006.

b Undivided including Jharkhand for the years 1986 and 1996.

c Undivided including Chhattisgarh for the years 1986 and 1996.

d Undivided including Uttarakhand for the years 1986, 1996, and 2006.

Source: Total fertility rate from the annual statistical report of the Sample Registration System of India.

Improved child survival and concurrent expansion of female education have led to fertility decline in developing countries like India (Davis, 1963 ; Dyson, 2010 ). We have already discussed geographic diversity in the TFR and transition. In Table 10 , we present the levels of TFR by education for India and selected states. In 1992–1993 , the TFR for India was 4.3 per woman for women who had completed fewer than 5 years of schooling (including nonliterate) compared to 3.3 for those who had 10 or more years of schooling; a difference of one child. By 2015–2016 , the TFR declined to 2.9 per woman and 1.8 for the respective groups. Over time there is no convergence in the level of fertility in lower and higher education groups as TFR declined by 45.5% among those who had 10 or more years of schooling compared to 32.6% among those who had fewer than 5 years of schooling. Nationally, around 22% of women aged 15–49 had completed 10 or more years of schooling in 1992–1993 . The share of these women increased to about 60% in 2015–2016 . Although TFR is higher for less educated people in India, their share in total women aged 15–49 has been reducing rapidly due to the expansion of education. The rise in education has a significant impact on delay in age at marriage.

A similar trend is observed at the state level as well. In 2015–2016 , with the exception of Bihar (TFR = 2.3), women who had 10 or more years of schooling had reached the replacement level of fertility. The lowest being in Punjab (TFR = 1.4) and the highest in Uttar Pradesh (TFR = 2.0). Women with 5–9 years of schooling in many states except Bihar, Madhya Pradesh, Rajasthan, and Uttar Pradesh either reached replacement or below-replacement level fertility or are very close to achieving it. The four larger states (Bihar, Madhya Pradesh, Rajasthan, and Uttar Pradesh) have lower child survival and limited outreach of female education. In 2015–2016 , Kerala had 95% of women aged 15–49 with 10 or more years of schooling, which was 44% in Bihar (including Jharkhand), 46% in Rajasthan, 52% in Madhya Pradesh (including Chhattisgarh), and 53% in Uttar Pradesh (including Uttarakhand).

Table 10. Total Fertility Rate by the Educational Status of the Women, India and Selected States, 1992–2016

a Undivided including Telangana (1992–1993, 1998–1999, and 2005–2006).

b Undivided including Jharkhand (1992–1993 and 1998–1999).

c Undivided including Chhattisgarh (1992–1993 and 1998–1999).

d Undivided including Uttarakhand (1992–1003 and 1998–1999).

Source : International Institute for Population Sciences ( 1993 ); International Institute for Population Sciences & ICF ( 2017 ); International Institute for Population Sciences & ORC-Macro ( 2000 ); International Institute for Population Sciences & ORC-Macro ( 2007 ).

The mortality data has information on three key indicators: infant mortality rate (IMR), under-5 mortality rate (U5MR), and expectation of life at birth (LEB; e o o ). The data comes from the SRS for India and covers about 25 years ( 1990–2016 ). The year 1990 is chosen as a base since it benchmarks the Millennium Development Goals (MDG) base year, and the year 2016 benchmarks the base year of the recently declared Sustainable Development Goals (SDGs). The MDG goal for U5MR for India was to attain a U5MR of 42 deaths of children aged below 5 years per 1,000 live births by the year 2015 . The corresponding goal for the IMR was 37 infant deaths per 1,000 live births. Under the SDG, the goals are 21 and 15, respectively, for the year 2030 .

At the beginning of the 20th century , in India, a newborn baby had an average life expectancy of 21–23 years (Davis, 1951 ; Mukherji, 1976 ). The SRS life table available for the period 2013–2017 revealed that a newborn baby in India would live an average of more than 69 years, which is considerably lower than in other countries globally and in the South Asian region. Nonetheless, this is a significant improvement from just about 20 years to close to 70 years, and an essential aspect of this improvement relates to IMR. At the national level, the IMR was 80 infant deaths per 1,000 live births in 1990 , which declined to 68 in 2000 (12 points in 10 years; see Table 11 ). The first decade of the 21st century unfolded a significant decline in the IMR for India— 47 infant deaths per 1,000 live births in 2010 and 34 per 1,000 in 2016 . Mortality decline in India and its states may have been due to improvements in access to health services and also an incremental increase in access to improved drinking water and sanitation. Similar to the global evidence (Fink et al., 2011 ), the National Family Health Survey (NFHS) data for 1992–1993 and 2015–2016 revealed a quantum jump in access to sanitation facilities (IIPS, 1993 ; IIPS & ICF, 2017 ).

The acceleration, especially after 2005 , may be due to the Janani Suraksha Yojana program implemented under the National Health Mission (erstwhile known as the National Rural Health Mission). The program provided a cash incentive of Rs. 1400 to women who delivered their babies in a health facility (Stephen et al., 2010 ). However, compliance varies considerably across India’s states. In the year 1990 , Kerala had the lowest IMR (17 infant deaths per 1,000 live births), whereas it was higher in Odisha (122), followed by Madhya Pradesh (111) and Uttar Pradesh (99). By 2016 , IMR declined significantly in all states. While Kerala continued to occupy the first place with the lowest IMR, Madhya Pradesh replaced Odisha with an IMR of 47 deaths per 1,000 live births. The states, on the whole, have succeeded in reducing the IMR; however, the usual lagging states of Assam, Bihar, Madhya Pradesh, Rajasthan, Uttar Pradesh, and Odisha continue to have higher IMRs.

Table 11. Infant Mortality Rate and Percentage Change in the Rate in India and Selected States, 1990–2016

a Undivided including Telangana for the years 1990, 1995, 2005, and 2010

b Undivided including Jharkhand for the years 1990 and 1995.

c Undivided including Chhattisgarh for the years 1990 and 1995.

d Undivided including Uttarakhand for the years 1990 and 1995.

Source: Infant mortality rates from the annual statistical report of the Sample Registration System of India.

Table 12 presents the gender-specific U5MRs for India and states for 1990–2016 . An average of 114 children per 1,000 live births died in India in 1990 before celebrating their 5th birthday, which declined to 39 in 2016 ; a two-thirds decline in 26 years. During the same period, the U5MR declined from 119 to 37 for male children and from 132 to 41 for female children. Similar to IMR, the U5MR fell relatively faster in the last 16 years in India ( 2000–2016 ) when compared with the corresponding change during 1990–2000 . Once again, there are vast differences across states of India in U5MR as well; the lagging states continue to have significantly higher levels of childhood mortality. In 2016 Kerala had the lowest U5MR (11), and the Madhya Pradesh had the highest (55), followed by Assam (52) and Odisha (50). The improvement in child survival in India brought a sense of security for the families to go for smaller families and contributed to the lowering of the TFR. An important point to note here is that regardless of the period studied, the U5MR in India has exceeded for female children compared to the male children. Surprisingly, most states have revealed a gender gap in childhood mortality. A study by Ram et al. ( 2013 , 2014 ) documented wide disparities in the levels of under-5 mortalities in districts of India.

Table 12. Gender-Specific Under-5 Mortality Rate and Percentage Change, India and Selected States, 1990–2016

a Undivided including Telangana for the years 1990, 1995, 2005, and 2010.

b Undivided including Jharkhand for the years 1990, 1995, 2005, and 2010.

c Undivided including Chhattisgarh for the years 1990, 1995, 2005, and 2010.

d Undivided including Uttarakhand for the years 1990, 1995, 2005, and 2010.

Source: Author calculations based on data from SRS Based Life Tables for 1988–1992, 1993–1997, 1998–2002, and 2003–2007. Data for 2015 and 2016 from the annual statistical report of the Sample Registration System of India for the respective years.

We now examine levels of life expectancy at birth (LEB). Table 13 presents the relevant data for India and its states for both sexes combined as well as separately. The LEB for India was nearly 49 years during 1970–1975 , which increased to about 58 years in 1986–1990 , an increase of 9 years in 16 years resulting in an annual improvement of approximately 0.6 years. By 1996–2000 , the LEB in India increased to 62 years and further to 69 years in 2013–2017 . Up until the 1980s, nationally, Indian males lived longer than the Indian females (Ram & Ram, 1997 ). Data on gender-specific LEB since 1993 indicates that in India, females now live longer than males, and the gap was by 2 years in 2013–2017 . The gender gap indeed widened in the mid-1990s when male LEB was at 60.4 years and females at 61.8 years. But at the same time, gender gaps in mortality have also widened for adolescents (to the female disadvantage), an anomaly indicating the downside of using only LEB for exploring gender disparity.

Table 13. Gender-Specific Life Expectancy at Birth and Changes in the Life Expectancy, India and Selected States, 1986–2017

$$ authors calculation using SRS gender-specific life tables.

b Undivided including Jharkhand for 1986–1990 and 1996–2000.

c Undivided including Chhattisgarh for 1986–1990 and 1996–2000.

d Undivided including Uttarakhand for 1986–1990, 1996–2000, and 2006–2010

Source: From Life tables of the Sample Registration System (SRS) of India.

Family Planning and Unmet Need

India acquired the status of being the first nation globally to launch an official family planning program in 1952 . However, the real push to the program came through in the 1960s when the program adopted a target-specific approach. The federal authorities in India assigned targets to the states, which were allocated to districts and further to the individual health workers at the lowest level of service provision. These targets became extremely volatile over the years, and the authorities announced disincentives and incentives to the users and the service providers based on performance (Pachauri, 2014 ). This period was accompanied by the emergency period ( 1975–1977 ) in India, when the program became extremely coercive. This act of the government damaged the program to a great extent and impacted the northern Hindi-speaking belt where fertility levels were higher. Although the success in fertility reduction in India is not comparable to that of other Asian countries, its achievements are by no means modest. In the initial phase, the program success was mostly monitored and evaluated using service statistics with the help of the number of acceptors and births averted as a result of family planning acceptance. Family planning surveys conducted in the 1970s and 1980s (ORG, 1972 , 1982 , 1990 ) complemented monitoring and evaluating efforts. After 1990 , India launched nationwide surveys (see IIPS, 1993 ; IIPS & ICF, 2017 ; IIPS & ORC-Macro 2000 , 2007 ). Tables 14 , 15 , and 16 give selected family planning indicators for India.

There has been a continuous rise in the percentage of married women using modern contraception in India. For example, just over 10% of married Indian women in 1970 used modern contraception (ORG, 1972 ). This percentage increased to 42.8% in 1998–1999 and to 48.5% in 2005–2006 (Table 14 ). India’s contraceptive prevalence rates (CPRs) are presented for the period between 1992–1993 to 2015–2016 in Table 13 . At the national level, overall CPR has increased from a little over 36% in the early 1990s to close to 48% in 2015–2016 , which translates to an increase of 12 units over the 23 years (an annual increase of 1.4%). The 2017 NFHS indicated that modern method CPR had marginally decreased from 48.5% in 2005–2006 to 47.8% in 2015–2016 (IIPS & ICF, 2017 ; IIPS & ORC-Macro, 2007 ). The decline in CPR of the modern method is substantial in many states, including Bihar, Gujarat, Karnataka, Kerala, Madhya Pradesh, and Tamil Nadu. This has raised debates among policy makers and researchers because these states have concurrently exhibited a significant decline in TFR levels. There is some research evidence that has indicated doubt about the estimated CPR for the period 2015–2016 . A study by Jayachandran and Stover ( 2018 ) expressed concern over the quality of contraceptive data collected in the 2017 NFHS. The modern limiting method CPR showed an increase of five units (from 31% to a little over 36%) and there was a twofold rise in the modern spacing method CPR (from about 6% to over 11%) during the same period. Interestingly, CPR for traditional methods also increased, from 4% to almost 6% (IIPS & ICF, 2017 ).

The levels of CPR, as well as the pace of change in it, varied considerably across Indian states included in the analysis. Generally, the states in the southern and western regions revealed higher levels of CPR compared to those in the northern and eastern regions of India. While the CPR rose over time, Gujarat and Kerala had a marginal decline in the overall CPR. Assam, Odisha, and West Bengal (all three in the eastern region) and Uttar Pradesh in the northern part had higher CPR of the traditional method (abstinence and withdrawal/rhythm) compared to the remaining states. While the CPR for traditional methods declined in Assam and West Bengal, it increased from 1%–2% in 1992–1993 to over 12%–14% in 2015–2016 in Odisha and Uttar Pradesh. The use of traditional methods is higher among women who live in urban areas, who were more educated and resided in economically better-off households. The patterns of CPR are somewhat similar for the modern limiting and spacing methods across states, as seen for all methods combined. Nonetheless, a few states, such as Assam, Haryana, Odisha, Uttar Pradesh, and West Bengal, have shown a tremendous rise in the CPR for modern spacing methods.

Table 14. Contraceptive Prevalence Rate for Modem Limiting, Modern Spacing Methods and Traditional Methods of Family Planning and Percentage Change in Them, India and Selected States, 1992–2016

a Undivided including Telangana (1992–1993).

c Undivided including Chhattisgarh (1992–1993).

d Undivided including Uttarakhand (1992–1993 and 1998–1999).

Tables 15 and 16 provide data on the future demand for family planning as assessed using the information on unmet need for family planning over 25 years. Nationally, the unmet need for family planning declined by nearly 37% in two and a half decades; the unmet need of almost 20% in 1992–1993 to about 13% in 2015–2016 (Table 15 ). The unmet need for modern spacing methods had halved in the country from nearly 12% to 6% during the same period. However, the unmet need for family planning seemingly has remained unchanged since 2010 , as the decline was by only one percentage point (from 14% to 13% for all methods and from 6.1% to 5.6% for spacing methods). Gujarat and Kerala were the only states where the total unmet need for family planning increased over time. In the remaining states, the change in the total unmet need has followed the national pattern. While the total unmet need remained nearly unchanged in Haryana, Karnataka, Madhya Pradesh, Maharashtra, and Tamil Nadu, it increased only marginally in Andhra Pradesh, Assam, and Wes Bengal. The unmet need doubled in Gujarat and increased substantially in Kerala.

In contrast, the unmet need declined in Bihar, Odisha, Rajasthan, and Uttar Pradesh during the same period. In case of unmet need for spacing methods, the data indicated substantial decline over the period for all states except Kerala, where unmet need for spacing methods rose from 6% to 8% in the last decade. A on-going investigation of NFHS data by Ram et al. ( in press ) showed that unmet need increased mainly due to the rise in the unmet need among the nonusers.

Table 15. Total Unmet Need for Family Planning, Unmet Need for Spacing, and Percentage Change, India and Selected States, 1992–2016

There are 46 million married women aged 15–49 in India who have expressed an unmet need for modern contraception, of whom 14 million prefer limiting methods and 18 million prefer spacing methods. The remaining 14 million couples, who used traditional methods, are considered to have an unmet need for modern methods of contraception in the NFHS for 2015–2016 (IIPS & ICF, 2017 ). It is important to note that all of the nonusers having unmet need will not convert into the users for various reasons as unmet need is highly unlikely to attain a zero value. The current unmet need of 18.7% may best reduce to 4%–5%, as observed in some states (as well as other countries in the neighborhood). In other words, 35 million couples actually can be converted to users. Nonuse of contraception could be due to sterility (primary and secondary), which varies considerably across India’s states, especially after age 30 (Ram, 2010 ). In other words, the potential pool of available users will include fewer people, around 28–30 million. Table 16 presents the share of current users and couples with unmet needs in the states of India in the national totals. The 14 states included consist of 88% of all users in India, and nearly 84% of the couples with unmet need belonged to these 14 states. Almost 47% of the couples with unmet need come from Bihar (13%), Madhya Pradesh (5%), Rajasthan (7%), and Uttar Pradesh (21%). This share is likely to rise because the demand for contraception in other states has almost reached a saturation point. The geographic allocation of unmet need creates a challenging situation because program strength and social development in these states are inadequate and of poor quality.

Table 16. State Share of the Users of Modern Methods of Family Planning and State Share of Couples Having Total Unmet Need for Family Planning (Limiting and Spacing Combined) in the National Totals, 1992–2016

A very dark side of Indian culture has been the practice of child marriage, which was rampant in the 20th century . The Hindu scripture advocated marriage for a girl before puberty (onset of menstruation). However, girls who married early remained in the parental home until “Gauna” (Kapadia, 1966 ), which was generally performed at the age when the girl attains physical maturity (onset of menstruation). The Sarda Act enacted in 1929 , followed by the Child Marriage Restraint Act of 1978 in India, defined the minimum legal age for marriage as 18 years for girls and 21 years for boys. Early marriage has a multidimensional effect on the lives of the females in India throughout their life course, from deprivation of education, skill development, health care access, and so on. At the macro level, the marriage pattern of a population has a significant effect on fertility and mortality (especially child mortality) levels. Marriage is one of the proximate determinants of fertility besides family planning use. The female age at marriage in India is rising, but rather slowly. The singulate mean age at marriage in India was 15.9 years in 1961 , which increased to 18.3 years in 1981 and 20.8 years in 2011 , an increase of about five years in five decades. In the 1990s, nearly half of the women aged 20–24 in India were married before age 18 years. This percentage reduced to about 45% in 2005–2006 .

The institution of marriage in India almost remained universal. Close to 97% of the Indian women aged 30–34 years in 2011 were married (Table 17 ). The percentage of these women varied marginally across states. Only two states (Kerala and Odisha) had 5% of the women aged 30–34 years who were single. The percentage of single women aged 30–34 years was 4% in Karnataka and West Bengal. Data from the 2015–2016 survey indicated that about one-quarter of women aged 20–24 years were married before they were 18 years (in absolute terms, 14.5 million women married below age 18). There is a great deal of variation across the states. Around 42% of women aged 20–24 years were married before age 18 in West Bengal, followed by 40% in Bihar, 31–33% in Rajasthan, Madhya Pradesh and Andhra Pradesh, and 23–26% in Gujarat, Karnataka, and Maharashtra.

Table 17. Percentage of Women Ages 20–24 Married Before Age 18 and Percentage of Single Women Ages 30–34, India and Selected States, 2015–2016

Source: Authors’ calculation based on data from NCP ( 2019 ) and IIPS and ICF ( 2017 ). Percent of single women data from Census of India, 2011.

Concluding Remarks

Although India holds a national treasure in its decadal censuses that have been continuously reported since 1881 , the country has failed to develop and strengthen its civil registration system for births and deaths. A significant constraint faced by Indian policy makers is a lack of data with regard to its socioeconomic and demographic scenario, including fertility and mortality. This shortcoming became apparent in several policies and programs that lacked evidence-based decisions to improve the health and well-being of the population. These experiences motivated the authorities in India, and nearly two decades after the country attained independence, the Government of India initiated the sample registration system SRS in an effort to replace the civil registration system and fill the data void. In the early 1990s, the government’s focus on health and well-being led to the publication of the first National Family Health Survey in 2017 . The data from these surveys has helped policy makers and researchers to gain insight into the demographic changes in India, nationally and subnationally.

India is the second-most populous country in the world. The international community has expressed concerns about the rising population size and high growth rate in India, which has received unprecedented attention in almost all platforms. Between 1961 and 2001 , India’s population grew at an average rate of about 2%, and the size of the population in absolute terms exceeded one billion in 2001 . During 2001–2011 , the population growth slowed down substantially. However, India continued to add an average of 18 million people annually to its already large base, leading to a total national population of 1.21 billion in 2011 . An assessment by the UN ( 2019 ) indicated that India’s population would peak at 1.65 billion in 2061 and would begin to decline after that and reach 1.44 billion in the year 2100 . The four large states in India (Uttar Pradesh, Bihar, Madhya Pradesh, and Rajasthan) continue to reveal high levels of fertility and mortality (especially during early childhood), and have great potential for future population growth. The spatial distribution of India’s population will have a significant influence on its future political and economic scenario. Kerala state may experience a negative population growth rate around 2036 . The undivided Andhra Pradesh (including the newly created state of Telangana) may experience the same around 2041 and Karnataka and Tamil Nadu around 2046 . Four states of Uttar Pradesh, Bihar, Madhya Pradesh, and Rajasthan would have 764 million people in 2061 (45% of the national total) by the time India’s population reaches around 1.65 billion (Verma, 2018 ).

Changes in fertility and mortality are the two most important demographic factors contributing to population growth in India. The total fertility rate (TFR) in India declined from about 6.5 children per woman in the early 1960s to 2.3 children per woman in 2016 (a reduction of 4.2 children per woman in fewer than six decades). India is concerned about relatively high TFR in Bihar (3.3 children per woman), Uttar Pradesh (3.1 children per woman), Madhya Pradesh (2.8 children per woman), and Rajasthan (2.7 children per woman). The states have exhibited a higher unmet need for contraception and a weak public health-care delivery system. Childhood mortality in India has declined substantially, especially after the 1990s (114 in 1990 to 39 children deaths per 1,000 live births in 2016 ). This remarkable improvement is the result of massive efforts to improve comprehensive maternal and child health programs and nationwide implementation of the national health mission. The latter focused attention on improving the maternal and child health indicators in the country. Despite this, childhood mortality continues to be unacceptably high in Uttar Pradesh (47 children deaths per 1,000 live births), Bihar (43 children deaths per 1,000 live births), Rajasthan (45 children deaths per 1,000 live births), and Madhya Pradesh (55 children deaths per 1,000 live births). Besides, more considerable attention to improving access to public health-care services would promote contraception use immensely by way of reducing unmet needs and, in turn, reduce child mortality.

Figure 5. Future prospects of the demographic transition for India, 1950–2100.

A great deal of scientific evidence suggests that the intertwined programmatic interventions focusing on female education and child survival are essential. Such efforts, notably in the four large states of Uttar Pradesh, Bihar, Madhya Pradesh, and Rajasthan, would go a long way to reduce unmet need for contraception and enhance contraception use giving a big push to reducing fertility in the future. This would be crucial for India to stabilize its population before reaching 1.65 billion. India’s demographic journey through the path of the classical demographic transition suggests that the country is very close to achieving replacement fertility. Figure 5 outlines the future path of India’s transition according to the UN’s ( 2019 ) assessment. Although India may achieve replacement level fertility very soon (around 2023 ), the population will continue to grow until 2060 due to population momentum. Only after this, India may experience a negative growth rate; that is, the crude death rate will exceed the crude birth rate.

Further Reading

• Caldwell, J. (1980). Mass education as a determinant of the timing of fertility decline. Population and Development Review , 6 (2), 225–255.
• Cleland, J. , & Rodriguez, G. (1988). The effect of parental education on marital fertility in developing countries. Population Studies , 42 , 419–442.
• Cochrane, S. H. (1979). Fertility and education: What do we really know? Johns Hopkins University Press.
• Dreze, J. , & Murthi, M. (2001). Fertility, education, and development: Evidence from India. Population and Development Review , 27 (1), 33–63.
• Lutz, W. , & Kebede, E. (2016). Education and health: Redrawing the Preston curve. Population and Development Review , 44 (2), 343–361.
• Pamuk, E. R. , Fuchs, R. , & Lutz, W. (2011). Comparing relative effects of education and economic resources on infant mortality in developing countries. Population and Development Review , 37 (4), 637–664.
• Preston, S. H. (1975). The changing relation between mortality and level of economic development . Population Studies , 29 (2), 231–248.
• Preston, S. H. (1980). Causes and consequences of mortality declines in less developed countries during the twentieth century. In R. A. Easterlin (Ed.), Population and economic change in developing countries (pp. 289–360). University of Chicago Press.
• Samir, K. C. , Wurzer, M. , Speringer, M. , & Lutz, W. (2018). Future population and human capital in heterogeneous India . Proceedings of the National Academy of Sciences , 115 (33), 8328–8333.
• Agarwala, S. N. (1964). Sterilisation as a population control device and its economics. The Economic Weekly , 1091–1094.
• Bongaarts, J. (2013). The implementation of preferences for male offspring. Population and Development Review , 39 (2), 185–208.
• Bongaarts, J. , & Guilmoto, C. Z. (2015). How many more missing women? Excess female mortality and prenatal sex selection, 1970–2050. Population and Development Review , 41 (2), 241–269.
• Chitre, K. T. (1964). Sterilization as a method of family limitation and its implementation in the family planning programme. Maharashtra Medical Journal , 11 (2), 288.
• Cleland, J. (2001). The effects of improved survival on fertility: A reassessment. Population and Development Review , 27 (Suppl.), 60–92.
• Cleland, J. , & Wilson, C. (1987). Demand theories of fertility decline: An iconoclastic view. Population Studies , 41 (1), 5–30.
• Coale, A. J. (1986). The decline of fertility in Europe since the 18th century as a chapter in demographic history. In A. J. Coale & S. C. Watkins (Eds.), The decline of fertility in Europe (pp. 1–31). Princeton University Press.
• Coleman, D. (2006). Immigration and ethnic change in low fertility countries: A third demographic transition. Population and Development Review , 32 (3), 401–446.
• Davis, K. (1951). The population of India and Pakistan . Princeton University Press.
• Davis, K. (1963). The theory of change and response in modern demographic history. Population Index , 29 (4), 345–366.
• Dyson, T. (1991). On the demography of South Asian famines, Part 1. Population Studies , 45 (1), 5–25.
• Dyson, T. (2010). Population and development: The demographic transition . Zed Books.
• Fink, G. , Gunther, I. , & Hill, K. (2011). The effect of water and sanitation on child health: Evidence from the demographic and health surveys 1986–2007. International Journal of Epidemiology , 40 , 1196–1204.
• Gopalaswamy, R. A. (1962). Family planning: Outlook for government action in India. In Cycle V. Kise (Ed.), Research in family planning (p. 78). Princeton University Press.
• Guilmoto, C. Z. , Saikia, N. , Tamrakar, V. , & Bora, J. K. (2018). Excess under-5 female mortality across India: A spatial analysis using 2011 census data. Lancet Global Health , 6 , e650–e658.
• International Institute for Population Sciences . (1993). National family health survey (NFHS-1), 1992–93: India . International Institute for Population Sciences.
• International Institute for Population Sciences & ICF . (2017). National family health survey (NFHS-4), 2015–16: India . International Institute for Population Sciences.
• International Institute for Population Sciences & ORC-Macro . (2000). National family health survey (NFHS-2), 1998–1999: India . International Institute for Population Sciences.
• International Institute for Population Sciences & ORC-Macro. (2007). National family health survey (NFHS-3), 2005–2006: India . International Institute for Population Sciences.
• Jayachandran, A. A. , & Stover, J. (2018). What factors explain the fertility transition in India? Health Finance and Governance Project.
• Jha, P. , Kesler, M. A. , Kumar, R. , Ram, F. , Ram, U. , Aleksandrowicz, L. , Bassani, D. G. , Chandra, S. , & Banthia, J. K. (2011). Trends in selective abortions of girls in India: Analysis of nationally representative birth histories from 1990 to 2005 and census data from 1991 to 2011. Lancet , 377 , 1921–1928.
• Kaa, D. J., van de . (1987). Europe’s second demographic transition. Population Bulletin , 42 (1), 1–59.
• Kaa, D. J., van de . (2002, January). The idea of a second demographic transitions in industrialized countries [Paper presentation]. Sixth Welfare Policy Seminar of the National Institute of Population and Social Security, Tokyo, Japan.
• Kapadia, K. M. (1966). Marriage and family in India . Oxford University Press.
• Kashyap, R. (2019). Is prenatal sex selection associated with lower female child mortality? Population Studies , 73 (1), 57–78.
• Kirk, D. (1996). Demographic transition theory. Population Studies , 50 (3), 361–387.
• Krishnamoorthy, S. (1997). India towards population and development goals, UNFPA for United Nations system in India . Oxford University Press.
• Landry, A. (1987). Adolphe Landry on the demographic transition revolution . Population and Development Review , 13 (4), 731–740.
• Laxmi, P. (1964). Family planning programme in madras state: The role of sterilisation as a method of family planning. Maharashtra Medical Journal , 11 (2), 271–272.
• Lesthaeghe, R. J. (2011). The “second demographic transition”: A conceptual map for the understanding of late modern demographic developments in fertility and family formation . Historical Social Research , 36 (2), 179–218.
• Lesthaeghe, R. J. (2014). The second demographic transition: A concise overview of its development . Royal Flemish Academy of Arts and Sciences.
• Lesthaeghe, R. J. , & Surkyn, J. (2004). When history moves on: The foundations and diffusion of a second demographic transition . Free University of Brussels.
• Mukherji, S. B. (1976). The age distribution of the Indian population: A reconstruction for the states and territories, 1881–1961 . East West Population Institute.
• National Commission on Population . (2019). Population projections for India and states 2011–2036 . Ministry of Health and Family Welfare, Technical Group on Population Projections.
• Notestein, F. W. (1945). Population: The long view. In T. Schultz (Ed.), Food for the world (pp. 36–57). University of Chicago Press.
• Operation Research Group . (1972). Family planning practices in India: First all India survey . Operation Research Group.
• Operation Research Group . (1982). Family planning practices in India: Second all India survey . Operation Research Group.
• Operation Research Group . (1990). Family planning practices in India: Third all India survey . Operation Research Group.
• Pachauri, S. (2014). Priority strategies for India’s family planning programme . Indian Journal of Medical Research , 140 (Suppl. 1), S137–S146.
• Pathak, K. B. , & Ram, F. (1981). Recent trends in the fertility of Asian Countries: A comparative analysis. In K. Srinivasan & S. Mukerji (Eds.), Dynamics of population and family welfare (pp. 118–151). Himalaya Publishing House.
• Pujari, S. B. , Joshi, S. K. , Bhatt, R. V. , & Patel, B. C. (1967, November 26–28). Complication following use of LIPPEs-loop [Paper presentation]. 14th All-India Obstetric and Gynaecological Congress, Nagpur, India.
• Rajan, S. L. (1994). Heading towards a billion. Economic and Political Weekly , 17 (24), 3201–3205.
• Ram, F. , Namboodiri, K. , & Ram, U. (1995). Fertility transition in India . International Institute for Population Sciences.
• Ram, F. , & Ram, U. (1997). Fertility transition in Uttar Pradesh and its neighboring states. In K. Gupta & A. Pandey (Eds.), Population and development in Uttar Pradesh (pp. 199–216). BR Publishing Corporation.
• Ram, F. , Verma, A. , Khan, N. , & Acharya, R. (2020). Assessment of death registration in India and selected states, 2000–16 [Unpublished report]. Population Council.
• Ram, F. , Kumar, A. , Saggurti, N. , & Jain, A. (in press). New estimates on demand for contraception in India and its states . Population Council.
• Ram, U. (2010). Levels and patterns of permanent childlessness in India and its states. Demography India , 39 (1), 81–101.
• Ram, U. , Jha, P. , Ram, F. , & Kumar, R. (2014). Absolute and relative declines in child mortality in India’s districts during 2001–12. Lancet Global Health , 2 , e21.
• Ram, U. , Jha, P. , Ram, F. , Kumar, K. , Awasthi, S. , Shet, A. , Pader, J. , Nansukusa, S. , & Kumar, R. (2013). Neonatal, 1–59 month, and under-5 mortality in 597 Indian districts, 2001 to 2012 . Lancet Global Health , 2 , e21.
• Ram, U. , & Ram, F. (2018). To be born and to be alive: The struggle of girl children in subregions of India. Lancet Global Health , 6 , e594–e595.
• Registrar General of India (n.d.-a). Provisional population totals, size, growth rate and distribution of population, census of India 2011 .
• Registrar General of India (n.d.-b). Provisional Population Totals, Gender Composition of the Population, Census of India 2011 .
• Registrar General of India (2020). Sample registration system statistical report for various years . Government of India.
• Seal, K. C. , & Talwar, P. P. (1994). The billion-plus population: Another dimension. Economic and Political Weekly , 29 (36), 2344–2347.
• Srinivasan, K. (2006). Population policies and family planning in India: A review and recommendations. Social Change , 37 (1), 125–136.
• Srinivasan, K. , & Pathak, K. B. (1981, December). The nature of stable high fertility and the determinants of its destabilization: Process in selected countries of Asia . International Population Conference of the IUSSP, Manila.
• Stephen, S. L. , Dandona, L. , Hoisington, J. A. , James, S. L. , Hogan, M. C. , & Gakidou, E. (2010). India’s Janani Suraksha Yojana, a conditional cash transfer programme to increase births in health facilities: An impact evaluation . Lancet , 375 (9730), 2009–2023.
• Thompson, W. S. (1929). Population . American Journal of Sociology , 34 (6), 959–975.
• United Nations . (1987, September). Global trends and prospects of the age structure of population: Different paths to aging . Proceedings of the UN International Symposium on Population, Structure and Development, Tokyo.
• United Nations . (2019). World population prospectsI . United Nations Department of Economic and Social Affairs.
• Verma, R. K. (2018). Convergence to population stability in India: A state-wise assessment of demographic potential and demographic dividend (Unpublished doctoral dissertation, International Institute for Population Sciences (IIPS)).
• Visaria, P. , & Visaria, L. (1994). Demographic transition, accelerating fertility decline in 1980 . Economic and Political Weekly , 29 (51–52), 3281–3292.
• Yadav, A. K. , & Ram, F. (2019). There is a glaring gender bias in death registrations in India. Economic and Political Weekly , 54 (51), 2349–8846.
• Zachariah, K. C. (1983). Anomaly of fertility decline in Kerala (Report No. 1, RPO 677–670). World Bank.

Related Articles

• Sexual and Reproductive Health in India
• Bioethics and Reproduction with Insights from Uruguay

Printed from Oxford Research Encyclopedias, Global Public Health. Under the terms of the licence agreement, an individual user may print out a single article for personal use (for details see Privacy Policy and Legal Notice).

date: 01 June 2024

• Cookie Policy
• Privacy Policy
• Legal Notice
• Accessibility
• [66.249.64.20|185.66.14.133]
• 185.66.14.133

Character limit 500 /500

Transitioning Tides: a Deep Dive into Stage 2 Demographic Shifts

This essay about the transformative Stage 2 of demographic transition, a pivotal period marked by declining mortality rates and sustained high birth rates. It explores the interplay of factors driving this shift, including advances in healthcare, economic development, and cultural norms. While Stage 2 brings opportunities for economic growth and innovation, it also poses challenges such as strain on resources and environmental degradation. Advocacy for family planning and education emerges as crucial amid the demographic turbulence. Ultimately, the essay underscores the need for thoughtful navigation through this stage, balancing economic progress with sustainability and societal well-being.

How it works

In the vast ocean of societal evolution, there exists a pivotal stage known as Stage 2 of the demographic transition. This phase marks a profound shift in the demographic landscape, akin to the changing tides that shape the coastline. Understanding the intricate dynamics of this transition unveils a tapestry of interconnected factors that sculpt the path of nations as they traverse through this transformative period.

At the heart of Stage 2 lies the interplay between mortality and fertility rates, two forces that wield significant influence over population dynamics.

The decline in mortality rates during this stage is akin to a beacon of hope illuminating the horizon. Advances in medical technology, coupled with improvements in public health infrastructure, form the bedrock upon which this decline is built. Vaccines, antibiotics, and sanitation measures act as guardians, warding off the specter of infectious diseases and ensuring that more individuals reach adulthood.

However, amidst the triumph of decreased mortality, the fertility rates stand as a steadfast companion, refusing to yield to the winds of change. Cultural norms, economic imperatives, and historical legacies intertwine to sustain high birth rates, anchoring societies to their past while charting a course for the future. Families, buoyed by notions of tradition and economic security, continue to navigate the waters of parenthood, undeterred by the shifting currents of modernity.

Economic winds gust through the sails of demographic transition, propelling nations towards the shores of urbanization and industrialization. The promise of prosperity beckons rural dwellers to urban centers, where opportunities for employment and advancement abound. Cities swell with newcomers seeking to carve out a better future, their footsteps echoing the rhythm of progress. Yet, amidst the bustling streets and towering skyscrapers, strains on infrastructure and resources emerge, casting shadows on the horizon.

The repercussions of Stage 2 reverberate across the societal landscape, leaving an indelible mark on the fabric of nations. Economically, a burgeoning population can breathe new life into stagnant industries, fueling innovation and productivity. The labor force expands, markets flourish, and consumer demand surges, creating a fertile ground for economic growth. However, the shadows of overpopulation loom large, casting doubts on the sustainability of such growth.

Environmental concerns add another layer of complexity to the narrative, as the footprint of human activity grows ever larger. Rising populations place unprecedented pressure on natural resources, leading to overexploitation and degradation of ecosystems. Urban sprawl encroaches upon once-pristine landscapes, leaving scars that may never fully heal. The delicate balance between human prosperity and environmental stewardship hangs in the balance, demanding thoughtful navigation through uncharted waters.

Amidst the turbulence of Stage 2, voices advocating for change begin to resonate, like beacons in the foggy night. Calls for family planning and education echo through the corridors of power, seeking to empower individuals with the tools to shape their own destinies. Governments and organizations rally behind initiatives aimed at promoting reproductive health and gender equality, recognizing the pivotal role they play in shaping the future trajectory of nations.

As nations navigate the tumultuous waters of Stage 2, the journey is fraught with challenges and opportunities alike. Each wave that crashes against the shore carries with it the potential for growth, transformation, and renewal. By charting a course guided by principles of sustainability, equity, and compassion, nations can weather the storms of demographic transition and emerge stronger, more resilient, and more united than ever before.

Cite this page

Transitioning Tides: A Deep Dive into Stage 2 Demographic Shifts. (2024, May 28). Retrieved from https://papersowl.com/examples/transitioning-tides-a-deep-dive-into-stage-2-demographic-shifts/

"Transitioning Tides: A Deep Dive into Stage 2 Demographic Shifts." PapersOwl.com , 28 May 2024, https://papersowl.com/examples/transitioning-tides-a-deep-dive-into-stage-2-demographic-shifts/

PapersOwl.com. (2024). Transitioning Tides: A Deep Dive into Stage 2 Demographic Shifts . [Online]. Available at: https://papersowl.com/examples/transitioning-tides-a-deep-dive-into-stage-2-demographic-shifts/ [Accessed: 1 Jun. 2024]

"Transitioning Tides: A Deep Dive into Stage 2 Demographic Shifts." PapersOwl.com, May 28, 2024. Accessed June 1, 2024. https://papersowl.com/examples/transitioning-tides-a-deep-dive-into-stage-2-demographic-shifts/

"Transitioning Tides: A Deep Dive into Stage 2 Demographic Shifts," PapersOwl.com , 28-May-2024. [Online]. Available: https://papersowl.com/examples/transitioning-tides-a-deep-dive-into-stage-2-demographic-shifts/. [Accessed: 1-Jun-2024]

PapersOwl.com. (2024). Transitioning Tides: A Deep Dive into Stage 2 Demographic Shifts . [Online]. Available at: https://papersowl.com/examples/transitioning-tides-a-deep-dive-into-stage-2-demographic-shifts/ [Accessed: 1-Jun-2024]

Don't let plagiarism ruin your grade

Hire a writer to get a unique paper crafted to your needs.

Our writers will help you fix any mistakes and get an A+!

Please check your inbox.

You can order an original essay written according to your instructions.

Trusted by over 1 million students worldwide

1. Tell Us Your Requirements

2. Pick your perfect writer

3. Get Your Paper and Pay

Hi! I'm Amy, your personal assistant!

Don't know where to start? Give me your paper requirements and I connect you to an academic expert.

short deadlines

100% Plagiarism-Free

Certified writers