problem solving with circle

Area of a Circle Practice Questions

Click here for questions, click here for answers.

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Circles Mixed Exercises

Area, circumference, diameter and radius

Area and circumference both relate to the radius and diameter of a circle. Once you know one, you can find all of the others -- It just takes a little math!

Practice Problems

If a circle's diameter is 10, calculate its circumference and area ?

Circumference = Π×diameter = 10 Π

radius = diameter ÷ 2 = 10 ÷ 2 = 5

A circle's area is 16Π. What is its circumference ?

Circumference = 2Π × radius = 2Π × 4 = 8Π

If a circle has a circumference of 26Π, what is its area .

Area = Π(radius)² = Π(13)² = 169Π

Interesting Fact about Circumference and Area

More interesting math facts here !

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• Math Article
• Problems On Circles

Problems On Area And Circumference Of A Circle

Before looking at problems on a circle based on perimeter and area, we need to understand the meaning of a circle and both the properties of the circle. In geometry, a circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called the centre. Let’s have a look the definitions of perimeter and area given below:

Perimeter Definition

Perimeter is associated with any closed figure like triangle , quadrilateral, polygons or circles. It is the measure of distance covered while going around the closed figure on its boundary.

For example, the perimeter of a square of side 2 cm = 8 cm, as we know that the square comprises 4 sides having equal lengths, thus the total distance covered will be 4×2, which will be the total length (i.e. perimeter).

Area Definition

Area means the actual space enclosed by a closed figure (or within the perimeter), and it means all the points within the closed figure and not the boundary.

Perimeter and Area of Circle Formula

Now, coming to the perimeter of a circle, as explained above, is the measure of distance going around the circle’s boundary. This distance is difficult to calculate precisely, and it is easy to visualize that the distance to go around is larger in a larger radius than a smaller radius. Hence, the perimeter is a function of the radius of a circle. In the case of the circle, we generally use the term “CIRCUMFERENCE” instead of the perimeter.

It is given by,

Circumference = 2πr

Here, r is a radius, and π is a constant defined as the ratio of circumference to the circle’s diameter.

The value of π is 22/7 or 3.1416

Also check: Circumference of a circle

The formula to find the area of a circle is given as:

Solved Problems on Circle

Let us understand the concepts related to circles along with the following questions-

To cover a distance of 10 km, a wheel rotates 5000 times. Find the radius of the wheel.

Number of rotations = 5000.

Total distance covered = 10 km

Let ‘r’ be the radius of the wheel.

Circumference of the wheel = Distance covered in 1 rotation = 2πr.

In 5000 rotations, the distance covered = 10 km = 1000000 cm.

\(\begin{array}{l}\text{Hence, in 1 rotation, the distance covered = }\frac{1000000}{5000}cm=200\: cm\end{array} \)

But this is equal to the circumference. Hence, 2πr = 200 cm

Taking the approximate value of π as 22/7, we get

r = 100 x 7/22

r = 31.82 cm approx.

The diameter of a semicircular shape is 14 cm. What will be the perimeter of this shape?

Diameter of semicircle = d = 14 cm

Radius = r = d/2 = 14/2 = 7 cm

Perimeter of semicircle = (Perimeter of circle/2) + d

= (2πr/2) + d

= (22/7) × 7 + 14

The difference between the circumference and the diameter of a circular bangle is 5 cm. Find the radius of the bangle. (Take π = 22/7)

Solution: Let the radius of the bangle be ’r’

According to the question:

Circumference – Diameter=5 cm

We know, Circumference of a circle = 2πr

Diameter of a circle = 2r

Therefore, 2πr – 2r =5 cm

2r(π-1) = 5 cm

\(\begin{array}{l}2r(\frac{22}{7}-1)=5cm\\ \\ 2r\times \frac{15}{7}=5\\ \\ r=\frac{5\times 7}{15\times 2}\\ \\ r=1.166cm\end{array} \)

The radius of bangle is 1.166 cm.

A girl wants to make a square-shaped figure from a circular wire of radius 49 cm. Determine the sides of a square.

Solution: Let the radius of the circle be ’r’.

Length of the wire=circumference of the circle= 2πr

\(\begin{array}{l}= 2\times \frac{22}{7}\times 49=2\times 22\times 7\\ \\ =308\: cm\end{array} \)

Let the side of the square be ‘s’.

Perimeter of the square = length of the wire = 4s

\(\begin{array}{l}s=\frac{308}{4}\\ \\ s=77\:cm\end{array} \)

Therefore, the sides of the square is 77 cm.

Find the area of a circular region whose radius is 21 m.

Radius of circular region = r = 21 m

Area of a circle = πr 2

= (22/7) × 21 × 21

= 22 × 3 × 21

= 1386 sq. m

Therefore, the area of the circular region is 1386 sq. m.

Video Lessons on Circles

Introduction to circles.

Parts of a Circle

Area of a Circle

All about Circles

Learn more about Surface area & volumes of the figures with BYJU’S-The learning app.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

10 Hard Geometry Math Problems for Circle

• Math Problems / Geometry
• 10 mins read

In this article, I represent geometry math problems for circles involving various theorems and applications like the intersecting secant theorem, Pythagoras theorem, and sine rule. This is very useful for high school students, mainly grade 10 students. These problems are also very challenging for adults who love solving math problems.

Table of Contents

Chord and Tangents Geometry Math Problems

Problem 1 : A semicircle inscribed inside a quarter circle. Find the length of a chord of the quarter circle that is also a tangent of the semicircle.

From the figure, a semicircle is inscribed inside a quarter circle, and PB is both the chord of the quarter circle and the tangent of the semicircle. Find the length of chord PB if the circle’s radius is 30 cm.

Solution : To solve the problem, we start by redrawing the figure as shown below.

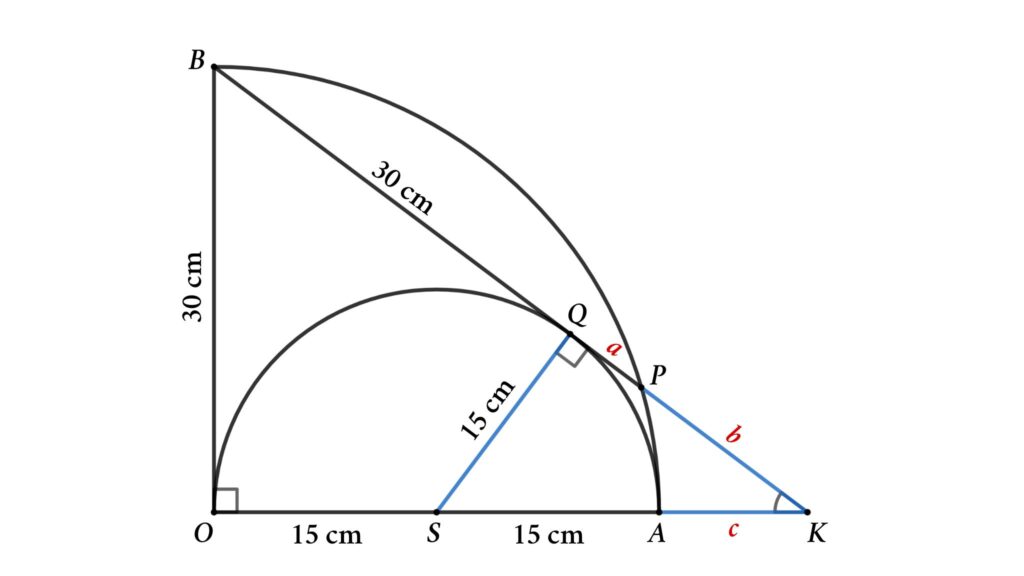
Here, SO = SA = SQ = 15 cm {radius of the semicircle}

OB = 30 cm ( radius of the quarter circle )

BQ = OB = 30 cm ( tangent from B)

Lets assume PQ = a , KP = b and AK = c

So, the length of the chord PB = BQ + QP = 30 + a

Consider △BOK and △QSK

Here △BOK and △QSK are similar triangles

∠OKB = ∠SKQ ( common for both triangles )

∠BOK = ∠SQK = 90°

OB/QS = OK/KQ = BK/KS

⇒ 30/15 = (30 + c )/( a + b ) = (30 + a + b )/(15 + c )

⇒ 2 = (30 + c )/( a + b ) = (30 + a + b )/(15 + c )

From, 2 = (30 + a + b )/(15 + c )

30 +2c = 30 + a + b

⇒ 2c = a + b

2 = (30 + c )/( a + b )

⇒ 2 a + 2 b = 30 + c

⇒ 4c = 30 + c

Then, 3 c = 30

Or, c = 10 cm

⇒ a + b = 2 c = 20 cm……………. eq (1)

In the next step, we turn the quarter circle into a circle (shown in the figure)

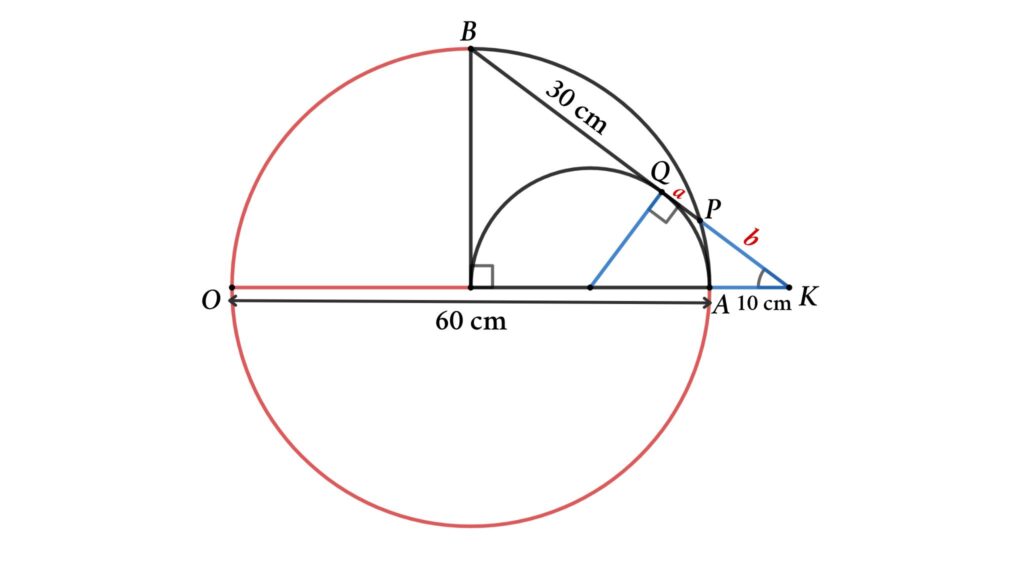
From figure

KA × KO = KP × KB ( Intersecting secants theorem )

⇒ 10 × (10 + 60) = b × (30 + a + b )

⇒ 10 × (70) = b × (30 + 20) { a + b = 20}

So, 700 = 50 b { a + b = 20}

⇒ b = 14 cm { a + b = 20}

a = 20 – 14 = 6 cm

Then, length of the chord PB = 30 + a = 30 + 6 = 36 cm

Problem 2 : From the figure, two semicircles are met at Q. AM = 4 cm is the radius of the smaller semicircle, and BN = 8 cm is the radius of the bigger semicircle. MN is the tangent of both semicircles. PQ is perpendicular to tangent MN, then find the length of this perpendicular line

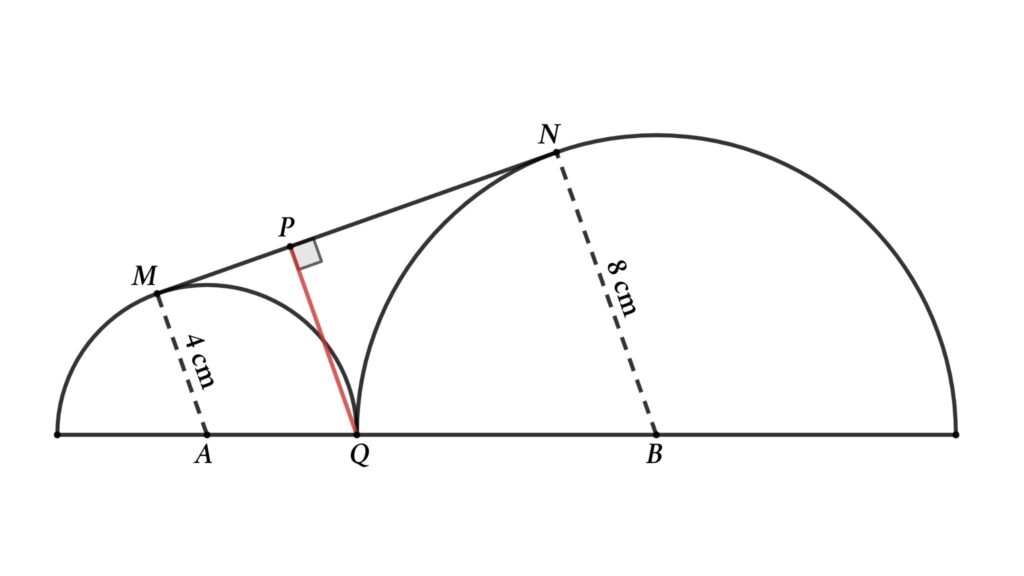
Solution : Let’s start by drawing a parallel line to AB. The line starts at M and ends at line BN.

Here, we get two triangles, △MPR and △MLN

From the figure

∠AMN = ∠MNB = 90° (MN is tangent of both semicircles )

AM = 4 cm ( radius of the smaller semicircle )

AM = RQ = BL = 4 cm (AM, PQ & BL parallel lines and AB is parallel to ML)

Now consider △MPR and △MLN

△MPR and △MLN are similar triangles

∠RMP = ∠MLN ( common for both triangles )

∠MPR = ∠MNL = 90° (PQ and NM are parallel lines )

PR/NL = MR/ML

⇒ PR/4 = 4/12

Or, PR/4 = 1/3

So, PR = 4/3 cm

⇒ PQ = RQ + PR = 4 + 4/3

⇒ PQ = 16/3 cm

That is, the length of the perpendicular line is 16/3 cm

Problem 3 : Determine the area and perimeter of the circle when the length of two parallel chords and the distance between them are given.

From the figure, AB and CD are two parallel chords of the circle. Here AB = 20 cm and CD = 8 cm and the distance between the codes is 12 cm. Then find the area and perimeter of the circle .

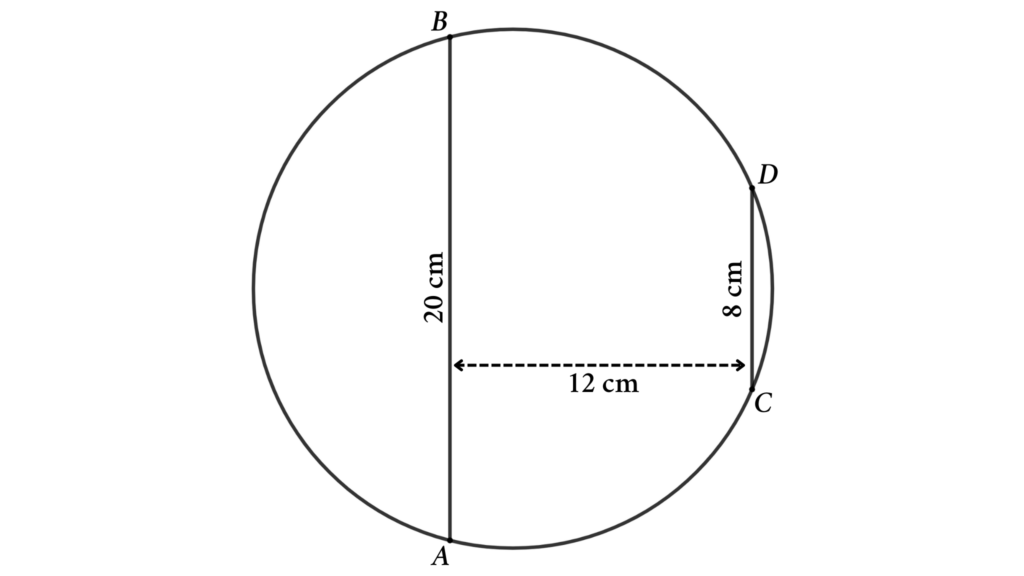
Solutions : Connect AC and BC and draw a perpendicular line PC from line AB to point C. Then we will get three triangles (△ABC, △PAC, and △PBC).

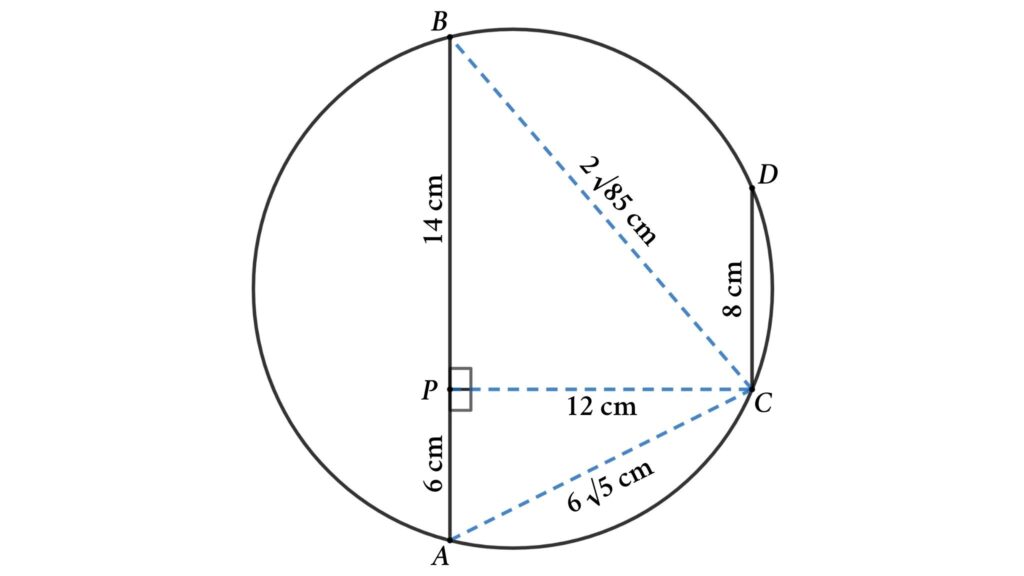
If the radius of the circumcircle is R , the area of the triangle is A , and the triangle’s sides are a , b , and c , then

$${A={{abc} \over 4R}}$$

Here PA = (AB – CD)/2 ( due to symmetry )

⇒ PA = (20 – 8)/2 = 6 cm

Apply Pythagoras’ theorem in △PAC

AB² = PA² + PC²

⇒ AB² = 6² + 12² = 36 + 144 = 180

⇒ AB = √180 = 6√5 cm

Now apply Pythagoras’ theorem in △PBC

BC² = PC² + PB²

⇒ BC² = 12² + 14² = 144 + 196 = 340

⇒ AB = √340 = 2√85 cm

Here, area of △ABC = \(1 \over 2\) · AB · PC = \(1 \over 2\) · 20 · 12 = 120 cm²

\({A={{abc} \over 4R}}\)

⇒ \({120={{20 \times 6\sqrt{5} \times 2\sqrt{85}} \over 4R}}\)

⇒ R = \(\sqrt{425} \over 2\) = \({5\sqrt{17}} \over 2\) cm

Area of the circle = π R ² = \(425 \pi \over 4\) cm²

Perimeter of the circle = 2π R = \(5\sqrt{17}\) cm

Problem 4 : When the length of three chords from a point is given, find the circle’s radius.

From the figure, PA, PB, and PC are chords of the circle. here PA = 8√3 cm, PB = 18 cm and PC = 10√3 cm. If ∠BPA = ∠BPC then find the radius of the circle.

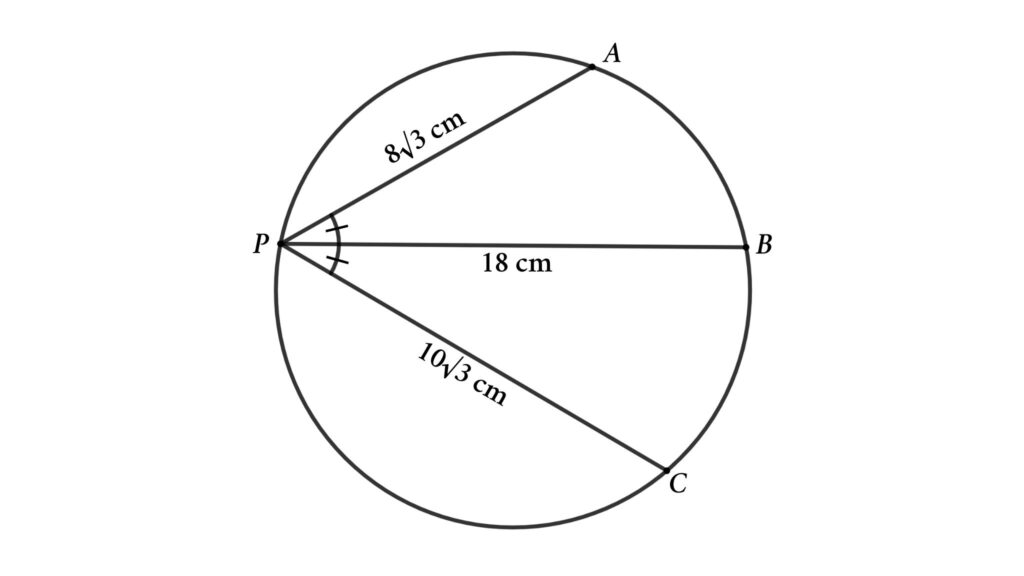
Solution : To solve the problem we start with connecting AB and CB. Here AB = CB because ∠BPA = ∠BPC and AB and CB are corresponding chords. Lets assume AB = CB = y and ∠BPA = ∠BPC = x

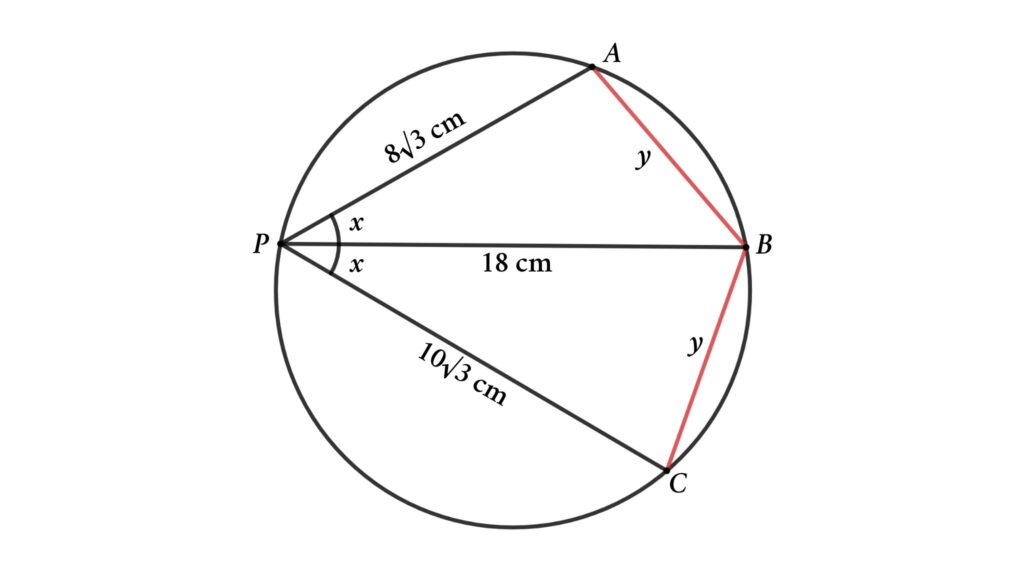
Here we have two triangles, we can apply the cosine rule for both triangles

AB² = PA² + PB² – 2 × PA × PB × cos ∠BPA

⇒ y ² = (8√3)² + 18² – 2 × 8√3 × 18 × cos x

Thus, y ² = 192 + 324 – 288√3 × cos x

⇒ y ² = 516 – 288√3 × cos x …………………………….. eq (1)

CB² = PC² + PB² – 2 × PC × PB × cos ∠BPC

⇒ y ² = (10√3)² + 18² – 2 × 10√3 × 18 × cos x

Thus, y ² = 300 + 324 – 360√3 × cos x

⇒ y ² = 624 – 360√3 × cos x …………………………….. eq (2)

From equation 1 and equation 2

516 – 288√3 × cos x = 624 – 360√3 × cos x

⇒ 72√3 × cos x = 108

⇒ cos x = (√3)/2 ……………………………………….eq(3)

y ² = 516 – 288√3 × cos x = 516 – 288√3 × (√3)/2

⇒ y ² = 516 – 432 = 84

so, y = √84

y = 2√21 ………………………eq(4)

From equation 3

⇒ cos x = (√3)/2

so, sin x = 1/2

by using the sine rule we get y /sin x = 2 R (∵ R is the radius of the circle )

y /sin x = 2 R (∵ R is the radius of the circle )

⇒ (2√21)/(1/2) = 2 R

⇒ R = 2√21 cm

So the radius of the circle is 2√21 cm

Triangle and Circle Math Problems

Problem 5 : Determine the area of the smaller circle inside a right triangle. The circle touches a semi-circle inscribed inside the triangle, and two of the triangle’s sides are tangents to the circle.

△ABC is a right triangle, as shown in the figure. Where AB = 8 cm and AC = 6 cm. If BC and AC are tangents to the circle and semicircle, then find the area of the circle.

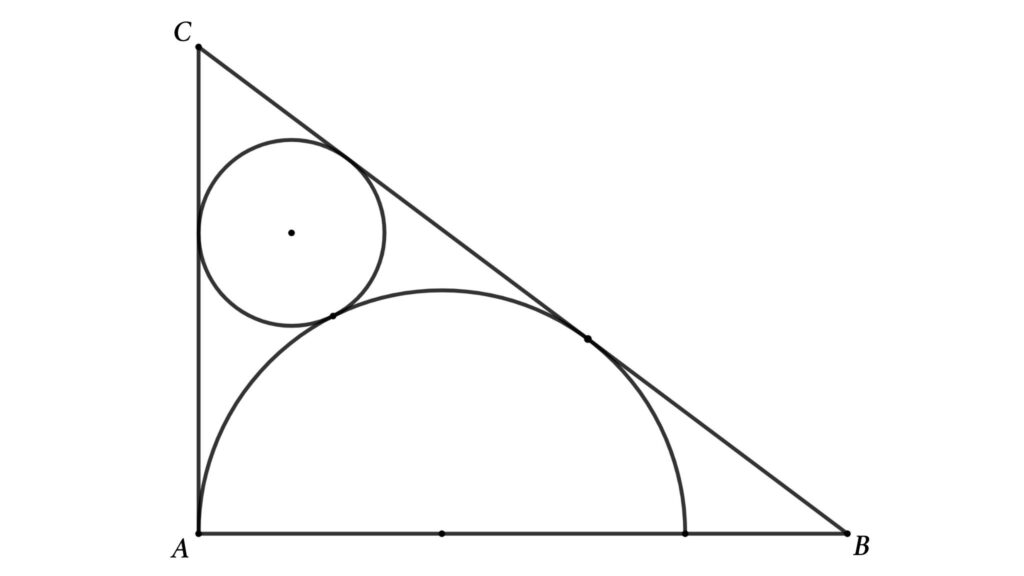
Solution : Assume the circle’s radius is r and the semicircle radius is R , and redraw the figure as shown below

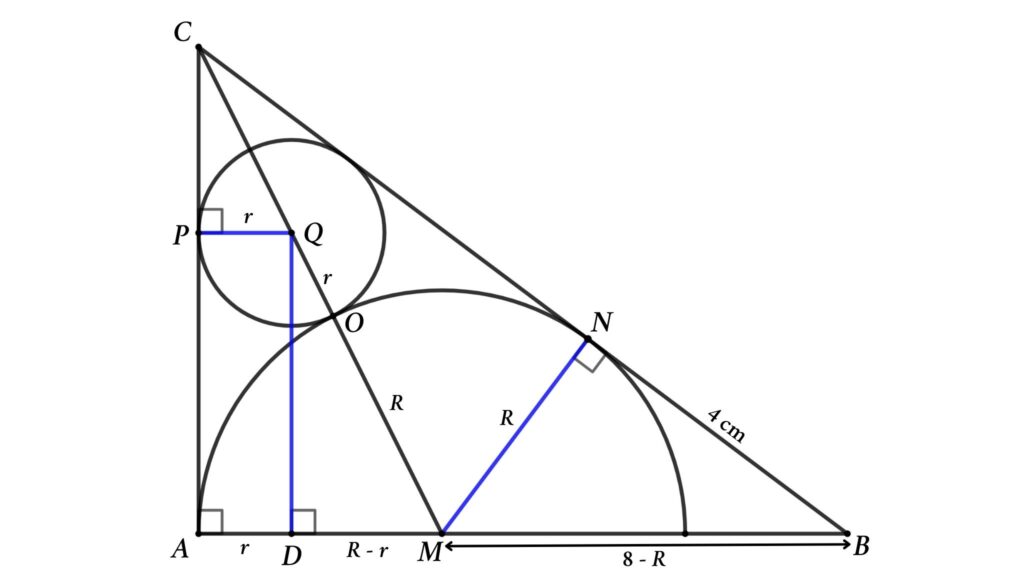
From the △ABC, using Pythagoras’ theorem we can find the length of BC

BC² = AB² + AC² = 8² + 6² = 64 + 36 = 100

Here, AC = MN = 6 cm ( tangent of the semicircle )

so, BN = 10 – 6 = 4 cm

Apply Pythagoras’ theorem in △MBN

BN² = BM² – MN²

⇒ 4² = (8 – R )² – R ²

⇒ 16 = 64 – 16 R + R ² – R ²

So, 16 R = 48

Then, R = 3 cm

Now apply Pythagoras’ theorem in △DMQ

DQ² = MQ² – DM²

⇒ DQ² = ( R + r )² – ( R – r )²

⇒ DQ² = R ² + 2 Rr + r ² – ( R ² – 2 Rr + r ²)

Thus, DQ² = 4 Rr

So, DQ = AP = \(2\sqrt{Rr}\) Here we get PC = 6 – \(2\sqrt{Rr}\)

Now consider △AMC and △QPC. Here PQ and AM are parallel lines so △AMC and △QPC are similar triangles, Then

PQ/AM = PC/AC

⇒ r / R = (6 – 2 √(R r ))/6

⇒ r /3 = (6 – 2 √(3 r ))/6

Then, r = 3 – √(3 r )

⇒ √(3 r ) = 3 – r

⇒ 3 r = (3 – r )²

Or, 3 r = 9 – 6 r + r ²

Then, r ² – 9 r + 9 = 0

This is a quadratic equation, so

$$ \begin{align} r &= {9 \pm \sqrt{9^2-4 \times 9 \times 1} \over 2} \ \end{align} $$

$$ \begin{align} r &= {9 \pm 3\sqrt{5} \over 2} \ \end{align} $$

Here r is less than 9, then

$$ \begin{align} r &= {9-3\sqrt{5} \over 2} \ \mathrm{cm}\ \end{align} $$

Then the area of the circle is \(\pi \bigg({9-3\sqrt{5} \over 2} \bigg)^2 \) or \({63 \pi-27 \pi \sqrt{5} \over 2} \ \mathrm{cm^2} \)

Problem 6 : When the sides of a triangle are given, find the area of the circumcircle.

In △ABC, AB = 8 cm, AC = 6 cm and BC = 4 cm. Then find the area of the circumcircle

Solution : If the radius of the circumcircle is R , the area of the triangle is A , and the triangle’s sides are a , b , and c , then

Now we can find the area of the triangle using Heron’s formula \({A=\sqrt{s(s-a)(s-b)(s-c)}}\)

Where s = ( a + b + c )/2

s = (8 + 6 + 4)/2 = 18/2 = 9

\({A=\sqrt{9(9-8)(9-6)(9-4)}}\) = \({\sqrt{9 · 1 · 3 · 5}}\) = 3√15 cm²

3√15 = (8 · 6 · 4)/(4 R )

R = 16/√15 cm

Then the area of the circumcircle is \(\pi \bigg({16 \over \sqrt{15}} \bigg)^2 \) or \({256 \pi \over 15} \ \mathrm{cm^2}\)

Square and Circle Math Problems

Problem 7 : Two squares are inscribed inside a quarter circle. Using the first square’s side length, determine the second square’s side length.

Two squares are inscribed inside a quarter circle. The larger square has a 2 cm side length. Calculate the side length of the smaller square

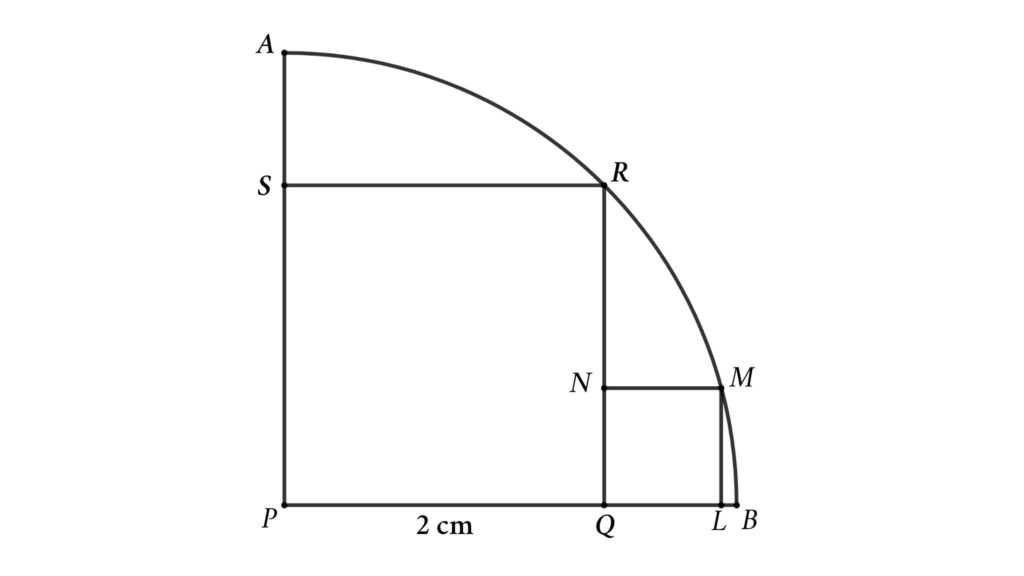
Solution : To solve the problem, let’s start with completing the quarter circle into a circle and extend RQ and MN. Assume the side length of the smaller square is x .

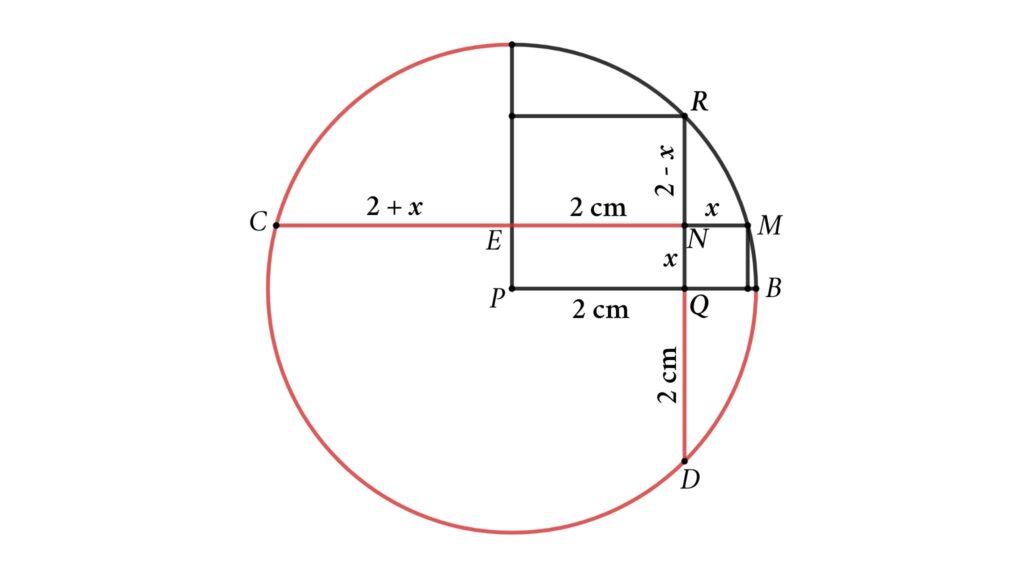
From the figure, we can see that chord CM and RD cross at N, so we get

CN × MN = RN × DN

EN = PQ = 2 cm

EM = EC = 2 + x ( due to symmetry )

⇒ CN = CE + EN = 2 + x + 2 = 4 + x

QR = QD = 2 cm

RN = RQ – NQ = 2 – x

DN = DQ + QN = 2 + x

CN × MN = RN × DN ( chord intersection theorem )

⇒ (4 + x ) × x = (2 – x ) × (2 + x )

⇒ 4 x + x ² = 4 – x ²

Then, 2 x ² + 4 x – 4 = 0

Or, x ² + 2 x – 2 = 0

$$ \begin{align} x &= {-2 \pm \sqrt{(-2)^2-4 \times 1 \times (-2)} \over 2} \ \end{align} $$

$$ \begin{align} x &= {-1 \pm \sqrt{4+8} \over 2} \ \end{align} $$

$$ \begin{align} x &= {-1 \pm \sqrt{3}} \end{align} $$

Where \( x>0 \) so, \(x = {\sqrt{3}-1} \ \mathrm{cm} \)

Or side length of the smaller square = \( {\sqrt{3}-1} \ \mathrm{cm}\)

Problem 8 : Determine the tangent length between the two quarter-circles enclosed by a square.

A square and two quarter-circles are in the figure. PQ is the tangent of both quarter circles. Find the length of PQ (length of tangent)

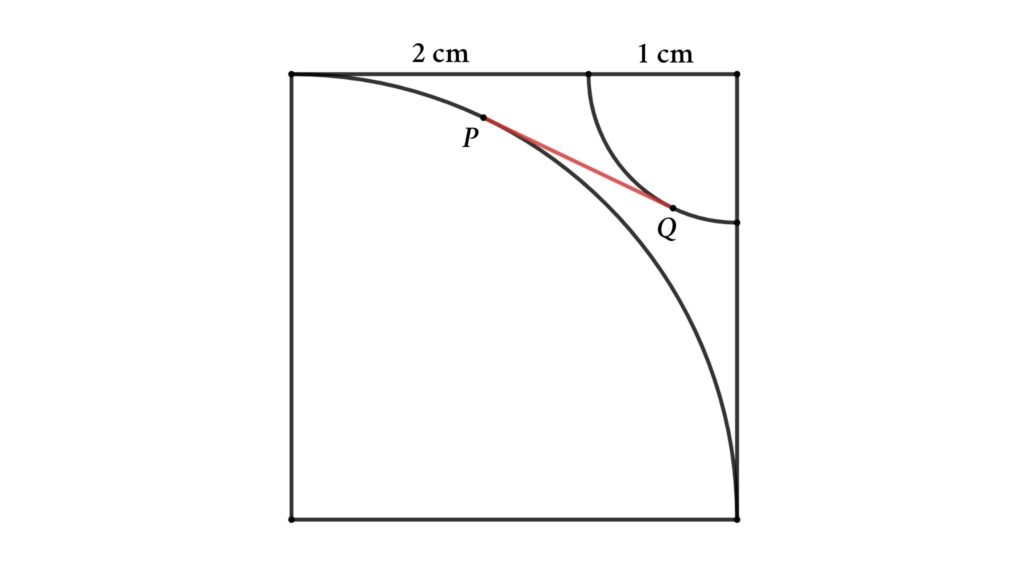
Solution : Create a right triangle shown in the figure (△ABC). Let’s assume the length of the tangent is x (PQ = x )

PQ || CB and PQ = CB = x

PC || BQ and PC = BQ = 1 cm

AB = 3√2 cm

Now apply Pythagoras’ theorem in △ABC

AB² = AC² + BC²

⇒ (3√2)² = (AP + PC)² + x ²

Or, (3√2)² = (3 + 1)² + x ²

⇒ 18 = 16 + x ²

⇒ x = √2 cm

That is the length of the tangent is √2 cm

Problem 9 : A semicircle and circle inscribed inside a square. Find the radius of the circle.

A circle and semicircle are inscribed inside a square as shown in the figure

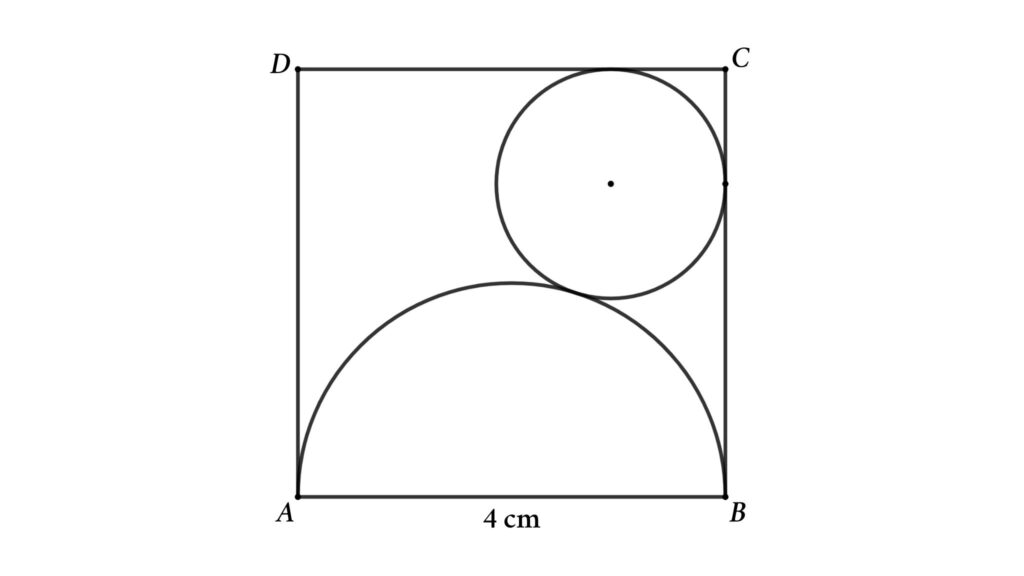
Find the radius of the circle if the side of the square is 4 cm.

Solution : Assume the radius of the circle is r and connect the center of the circle and semicircle to make a right triangle shown in the figure.

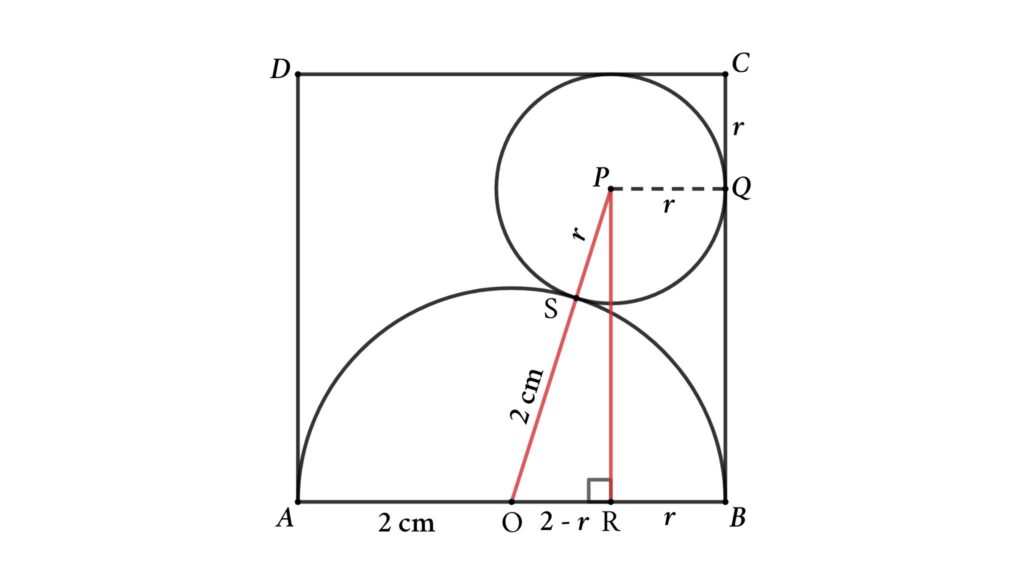
PQ = BR = PS = r ( radius of the circle )

OA = OB = OS = 2 cm ( radius of the semicircle )

OR = OB – BR = 2 – r

OP = OS + SP = 2 + r

Apply Pythagoras’ theorem in △OPR

PR² = OP² – OR²

⇒ PR² = (2 + r )² – (2 – r )²

⇒ PR² = 4 + 4 r + r ² – (4 – 4 r + r ²)

Thus, PR² = 8 r

⇒ PR = √(8 r )

⇒ BQ = √(8 r )

Here, BC = BQ + QC = √(8 r ) + r = 4

⇒ 8 r = (4 – r )²

⇒ 8 r = 16 – 8 r + r ²

Or, r ² – 16 r + 16 = 0

$$ \begin{align} r &= {-(-16) \pm \sqrt{(-16)^2-4 · 1 · 16} \over 2}\ \end{align} $$

$$ \begin{align} r &= {16 \pm 8 \sqrt{3} \over 2} = {8 \pm 4\sqrt{3}}\ \end{align} $$

Here radius of the circle is less than 4 so \(r = {8 – 4\sqrt{3}} \) cm

Problem 10 : A circle is inside a quarter-circle. Find the difference between areas.

A quarter circle with a radius of 6 cm is shown in the figure. A circle is drawn inside the quarter circle by touching the arc and one of its sides. Then find the area of the blue region.

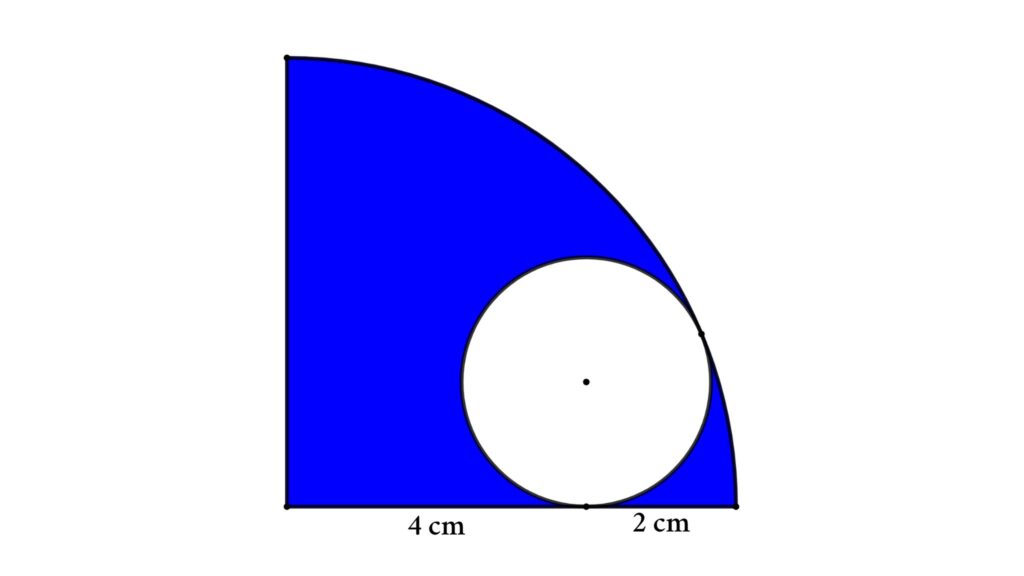
Solution : Assume the circle’s radius is r , and redraw the figure as shown below

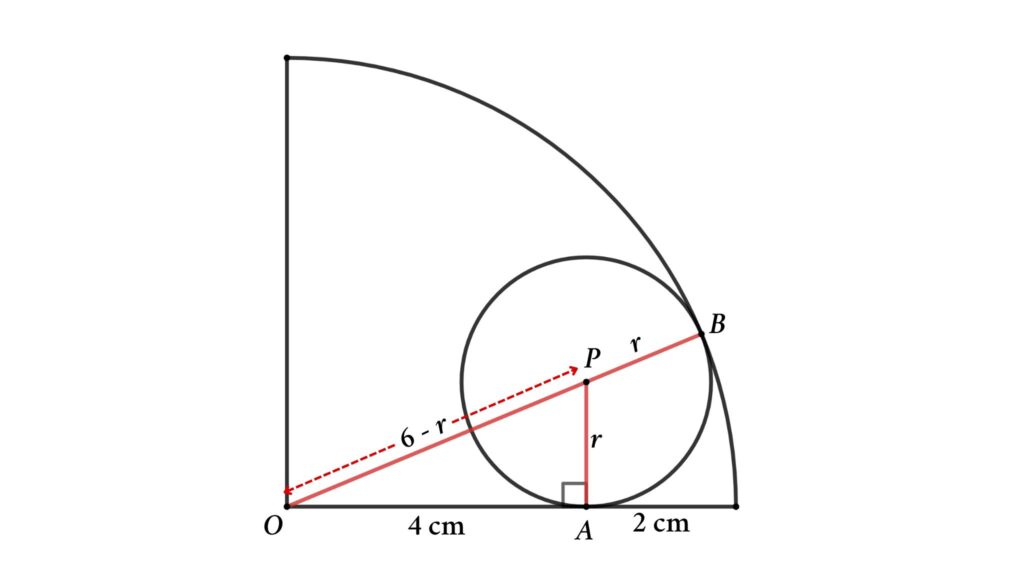
Here OB is the radius of the quarter circle so OB = 6 cm

OP = OB – PB = 6 – r

Now apply Pythagoras’ theorem in △OAP

OP² = OA² + AP²

⇒ (6 – r )² = 4² + r ²

⇒ 36 – 12 r + r ² = 16 + r ²

So, 12 r = 20

⇒ r = 20/12 = 5/3 cm

That is the radius of the circle is 5/3 cm

Share Share this content

• Opens in a new window Pinterest
• Opens in a new window X
• Opens in a new window Facebook
• Opens in a new window Reddit

You Might Also Like

How To Solve A System Of Quadratic Equations By Elimination?

Algebra Problem: System of Quadratic Equations in Two Variables

Find the Area of the Triangle Inside Three Circles

Leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• Post category: Math Problems / Geometry

Circle Problems - Radius, Diameter, Circumference and Area

Related Topics & Worksheets: Circles Circumference Of Circle Area Of Circle

Objective: I know how to calculate problems that involve the radius, diameter, circumference and area of circle.

The circumference of a circle is the distance around the circle. The formula is π d or 2π r

Read the lesson on circumference of circle if you need to learn how to calculate the circumference of a circle.

The area of a circle is size of the surface of the circle. The formula is π r 2 . The area of the circle is expressed in square units. Since the formula is only given in terms of radius, remember to change from diameter to radius when necessary. Read the lesson on area of circle if you need to learn how to calculate the area of a circle.  

We hope that the free math worksheets have been helpful. We encourage parents and teachers to select the topics according to the needs of the child. For more difficult questions, the child may be encouraged to work out the problem on a piece of paper before entering the solution. We hope that the kids will also love the fun stuff and puzzles.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Practice Problems
• Assignment Problems
• Show all Solutions/Steps/ etc.
• Hide all Solutions/Steps/ etc.
• The Definition of a Function
• Solving Equations and Inequalities
• Common Graphs
• Calculus II
• Calculus III
• Differential Equations
• Algebra & Trig Review
• Common Math Errors
• Complex Number Primer
• How To Study Math
• Cheat Sheets & Tables
• MathJax Help and Configuration
• Notes Downloads
• Complete Book
• Practice Problems Downloads
• Complete Book - Problems Only
• Complete Book - Solutions
• Assignment Problems Downloads
• Other Items
• Get URL's for Download Items
• Print Page in Current Form (Default)
• Show all Solutions/Steps and Print Page
• Hide all Solutions/Steps and Print Page

Section 3.3 : Circles

In this section we are going to take a quick look at circles. However, before we do that we need to give a quick formula that hopefully you’ll recall seeing at some point in the past.

Given two points \(\left( {{x_1},{y_1}} \right)\) and \(\left( {{x_2},{y_2}} \right)\) the distance between them is given by,

So, why did we remind you of this formula? Well, let’s recall just what a circle is. A circle is all the points that are the same distance, \(r\) – called the radius, from a point, \(\left( {h,k} \right)\) - called the center. In other words, if \(\left( {x,y} \right)\) is any point that is on the circle then it has a distance of \(r\) from the center, \(\left( {h,k} \right)\).

If we use the distance formula on these two points we would get,

Or, if we square both sides we get,

This is the standard form of the equation of a circle with radius \(r\) and center \(\left( {h,k} \right)\).

Okay, in this case we have \(r = 8\), \(h = - 4\) and \(k = 7\) so all we need to do is plug them into the standard form of the equation of the circle.

Do not square out the two terms on the left. Leaving these terms as they are will allow us to quickly identify the equation as that of a circle and to quickly identify the radius and center of the circle.

Graphing circles is a fairly simple process once we know the radius and center. In order to graph a circle all we really need is the right most, left most, top most and bottom most points on the circle. Once we know these it’s easy to sketch in the circle.

Nicely enough for us these points are easy to find. Since these are points on the circle we know that they must be a distance of \(r\) from the center. Therefore, the points will have the following coordinates.

In other words all we need to do is add \(r\) on to the \(x\) coordinate or \(y\) coordinate of the point to get the right most or top most point respectively and subtract \(r\) from the \(x\) coordinate or \(y\) coordinate to get the left most or bottom most points.

Let’s graph some circles.

• \({x^2} + {y^2} = 1\)
• \({x^2} + {\left( {y - 3} \right)^2} = 4\)
• \({\left( {x - 1} \right)^2} + {\left( {y + 4} \right)^2} = 16\)

In all of these all that we really need to do is compare the equation to the standard form and identify the radius and center. Once that is done find the four points talked about above and sketch in the circle.

In this case it’s just \(x\) and \(y\) squared by themselves. The only way that we could have this is to have both \(h\) and \(k\) be zero. So, the center and radius is,

Don’t forget that the radius is the square root of the number on the other side of the equal sign. Here is a sketch of this circle.

A circle centered at the origin with radius 1 ( i.e. this circle) is called the unit circle . The unit circle is very useful in a Trigonometry class.

In this part, it looks like the \(x\) coordinate of the center is zero as with the previous part. However, this time there is something more with the \(y\) term and so comparing this term to the standard form of the circle we can see that the \(y\) coordinate of the center must be 3. The center and radius of this circle is then,

Here is a sketch of the circle. The center is marked with a red cross in this graph.

For this part neither of the coordinates of the center are zero. By comparing our equation with the standard form it’s fairly easy to see (hopefully…) that the \(x\) coordinate of the center is 1. The \(y\) coordinate isn’t too bad either, but we do need to be a little careful. In this case the term is \({\left( {y + 4} \right)^2}\) and in the standard form the term is \({\left( {y - k} \right)^2}\). Note that the signs are different. The only way that this can happen is if \(k\) is negative. So, the \(y\) coordinate of the center must be -4.

The center and radius for this circle are,

Here is a sketch of this circle with the center marked with a red cross.

So, we’ve seen how to deal with circles that are already in the standard form. However, not all circles will start out in the standard form. So, let’s take a look at how to put a circle in the standard form.

• \({x^2} + {y^2} + 8x + 7 = 0\)
• \({x^2} + {y^2} - 3x + 10y - 1 = 0\)

Neither of these equations are in standard form and so to determine the center and radius we’ll need to put it into standard form. We actually already know how to do this. Back when we were solving quadratic equations we saw a way to turn a quadratic polynomial into a perfect square. The process was called completing the square .

This is exactly what we want to do here, although in this case we aren’t solving anything and we’re going to have to deal with the fact that we’ve got both \(x\) and \(y\) in the equation. Let’s step through the process with the first part.

We’ll go through the process in a step by step fashion with this one.

Step 1 : First get the constant on one side by itself and at the same time group the \(x\) terms together and the \(y\) terms together.

In this case there was only one term with a \(y\) in it and two with \(x\)’s in them.

Step 2 : For each variable with two terms complete the square on those terms.

So, in this case that means that we only need to complete the square on the \(x\) terms. Recall how this is done. We first take half the coefficient of the \(x\) and square it.

We then add this to both sides of the equation.

Now, the first three terms will factor as a perfect square.

Step 3 : This is now the standard form of the equation of a circle and so we can pick the center and radius right off this. They are,

In this part we’ll go through the process a little quicker. First get terms properly grouped and placed.

Now, as noted above we’ll need to complete the square twice here, once for the \(x\) terms and once for the \(y\) terms. Let’s first get the numbers that we’ll need to add to both sides.

Now, add these to both sides of the equation.

When adding the numbers to both sides make sure and place them properly. This means that we need to put the number from the coefficient of the \(x\) with the \(x\) terms and the number from the coefficient of the \(y\) with the \(y\) terms. This placement is important since this will be the only way that the quadratics will factor as we need them to factor.

Now, factor the quadratics as show above. This will give the standard form of the equation of the circle.

This looks a little messier than the equations that we’ve seen to this point. However, this is something that will happen on occasion so don’t get excited about it. Here is the center and radius for this circle.

Do not get excited about the messy radius or fractions in the center coordinates.

o          Circle

o          Radius

o          Diameter

o          Arc

o          Subtend

o          Sector

o          Chord

o          Secant

o          Tangent

o          Circumference

o          Know how to fundamentally define a circle

o          Identify various parts of circles

o          Calculate the area and circumference of a circle or portion thereof

Introduction to Circles

A circle is simply a figure defined by all the points that are equidistant from a given center point. Thus, we can define a circle (without a definite location) by specifying the distance from the center; alternatively, we can define a circle (with a definite location) by specifying the distance from and the location of the center. The distance from the center of the points that lie on the circle is called the radius (plural radii ) of the circle. A circle with a radius r and center point C is shown below.

Note that regardless of which point on the circle is chosen, it is always a distance r from the center point, C. Each of the line segments drawn from C to the circle is called a radius (in other words, no one segment is defined as the radius, since all such segments are equal in length). The circle itself does not show any angles or sides that we can use to determine how many degrees are in the figure (as we did with polygons), but we can see that any two radii do form an angle α , as shown below.

Using our measurement of degrees, this angle α can (unambiguously) be any value between 0° and 360°. We can also define angles with either positive or negative numbers, depending on the direction of measurement from a particular radius--a positive angle is traditionally measured in the counterclockwise direction, and a negative angle is traditionally measured in the clockwise direction, as shown below.

We can also identify other parts of a circle. Given any point P 1 on the circle, the most distant point P 2 that is also on the circle is on the exact opposite side, and these points are the length of two radii apart. The line segment that connects them passes through the center and is called the diameter of the circle.

Any two radii in the circle (which form an angle α ), such as those shown below, form an arc and a sector. The arc is the portion of the circle opposite to (or subtended by) the angle α and between the endpoints of the radii. The sector is the area enclosed by the arc and the radii. The arc A in the diagram below is shown as a bold line, and the sector S is shown as a shaded area.

Any line segment connecting two points on the circle is called a chord . Note that a diameter is a chord (the longest possible chord of a circle!). The chord D is shown below as a bold line.

Other special figures related to circles are secants and tangents. A secant is simply a line that intersects two points of the circle (a chord is a segment of a secant). A tangent is a line that intersects the circle at exactly one point. Secant E and tangent T are shown in the diagram below as bold lines.

Practice Problem : Identify each part (labeled A through E) of the circle below.

Solution : Each portion of the circle or other line can be identified by its relationship to the entire circle. Each of these figures is discussed and defined above. The shaded area A is a sector. The line (or line segment) B is a tangent (note that it intersects the circle at only one point). C is a diameter, D is a chord, and E is a radius.

Basic Characteristics of Circles

Now that we have identified some of the components of circles, we can now begin to derive some of their characteristics using the tools we have developed thus far. Some of the properties of circles require trigonometry to derive (such as the length of a chord subtended by an angle α ), but others we can derive or simply state basic formulas that we can use to solve problems. Let's start with the circumference and area of a circle. The circumference of a circle is simply the length of the boundary (that is, the perimeter) of the circle. We will simply state the formula for the circumference C of a circle in terms of the radius ( r ) or the diameter ( d ):

C = 2 πr = πd

Note that with the formula for the circumference, we introduce the number π . Because π is (most mathematicians think) an irrational number, we cannot write it out exactly in its decimal form, nor can we write it exactly as a fraction. We can, however, write a decimal estimation of π that is sufficient for our purposes.

π ≈ 3.1416

Many calculators have a built-in key for the number π (although the calculator still just uses an approximation of π ). For many calculations, an approximate π value of 3.14 yields sufficient accuracy. As it turns out, π also appears in the formula for the area of a circle. Let's write the area A in terms of the radius r .

A = πr 2

Note again that we have not really derived these formulas; we are simply stating them as fundamental facts upon which we will base the rest of our investigation of the characteristics of circles.

Practice Problem : Find the area and circumference of a circle with a diameter of 4 inches.

Solution : One of the first rules of solving these types of problems involving circles is to carefully note whether we are dealing with the radius or the diameter. In this problem, the circle is described using the diameter, which is 4 inches. The radius is thus 2 inches. Let's now calculate the area A and circumference C using the formulas given above.

A = πr 2 = π (2 in) 2 ≈ (3.14)(4 in 2 ) =12.56 in 2

C = πd = π (4 in) ≈ (3.14) (4 in) = 12.56 in

Coincidentally, the area and circumference have the same numerical values (but not the same units!). This is not generally the case, of course.

Let's take a look at the characteristics of other parts of a circle. For instance, now that we know how to calculate the circumference of a circle, we can also calculate the length of an arc (which is simply a portion of the circumference). An angle α defined by two radii subtends an arc. Let's take a look at several examples, from which we can identify a pattern. The arc K in each case is shown as a bold curve. The circumference of the circle is C .

The expressions under each example can be derived by inspection. We know that if the angle α is 90° (one-quarter of the full 360° of the circle), then the subtended arc is one-quarter of the circumference. The same reasoning applies to determining the arc length K for the other two cases as well. Thus, we can see that the arc length is related to the circumference as the angle α is related to 360°. But this is simply a ratio that we can write as follows.

Thus, the area of sector S is related to the area A according to the ratio of α to 360°. We can once again derive a formula.

Practice Problem : A central angle γ in a circle of radius 10 units forms a sector with an area of 2.62 square units. Find the measure of γ .

Solution : Let's start by drawing a diagram of the problem. This diagram need not be to scale-we can simply use it to more easily identify the parts of the circle discussed in the problem. We'll call the sector S , and we know S = 2.62 units 2 .

We can use the formula presented earlier to relate the area S of the sector to the area A of the circle.

But we also know how to calculate A using the given radius of 10 units.

A = π r 2 = π(10 units) 2 ≈ 3.14(100 units 2 ) ≈ 314 units 2

Now let's find γ .

Thus, the angle has a measure of 3°.

• Course Catalog
• Group Discounts
• Gift Certificates
• For Libraries
• CEU Verification
• Medical Terminology
• Accounting Course
• Writing Basics
• QuickBooks Training
• Proofreading Class
• Sensitivity Training
• Excel Certificate
• Teach Online
• Terms of Service
• Privacy Policy