accuracy precision and measurement homework answers

• Units Of Measurement
• Accuracy Precision Measurement

Accuracy and Precision - The Art of Measurement

Measurement is essential for us to understand the external world, and through millions of years of life, we have developed a sense of measurement. Measurements require tools that provide scientists with a quantity. The problem here is that the result of every measurement by any measuring instrument contains some uncertainty. This uncertainty is referred to as an error. Accuracy and precision are two important factors to consider while taking measurements. Both these terms reflect how close a measurement is to a known or accepted value. In this article, let us learn in detail about precision and accuracy.

The ability of an instrument to measure the accurate value is known as accuracy. In other words, it is the  the closeness of the measured value to a standard or true value . Accuracy is obtained by taking small readings. The small reading reduces the error of the calculation. The accuracy of the system is classified into three types as follows:

• Point Accuracy

The accuracy of the instrument only at a particular point on its scale is known as point accuracy. It is important to note that this accuracy does not give any information about the general accuracy of the instrument.

• Accuracy as Percentage of Scale Range

The uniform scale range determines the accuracy of a measurement. This can be better understood with the help of the following example: Consider a thermometer having the scale range up to 500 ºC . The thermometer has an accuracy of ±0.5 percent of scale range i.e. 0.005 x 500 = ± 2.5 ºC. Therefore, the reading will have a maximum error of ± 2.5 ºC.

• Accuracy as Percentage of True Value

Such type of accuracy of the instruments is determined by identifying the measured value regarding their true value. The accuracy of the instruments is neglected up to ±0.5 percent from the true value.

The closeness of two or more measurements to each other is known as the precision of a substance. If you weigh a given substance five times and get 3.2 kg each time, then your measurement is very precise but not necessarily accurate. Precision is independent of accuracy. The below examples will tell you about how you can be precise but not accurate and vice versa. Precision is sometimes separated into:

• Repeatability

The variation arising when the conditions are kept identical and repeated measurements are taken during a short time period.

• Reproducibility

The variation arises using the same measurement process among different instruments and operators, and over longer time periods.

Accuracy is the degree of closeness between a measurement and its true value. Precision is the degree to which repeated measurements under the same conditions show the same results.

Since you are here, you might want to check out the following articles:

• Errors in Measurement
• Measurement of length

Accuracy and Precision Examples

The top left image shows the target hit at high precision and accuracy. The top right image shows the target hit at a high accuracy but low precision. The bottom left image shows the target hit at a high precision but low accuracy. The bottom right image shows the target hit at low accuracy and low precision.

More Examples

• If the weather temperature reads 28 °C outside and it is 28 °C outside, then the measurement is said to be accurate. If the thermometer continuously registers the same temperature for several days, the measurement is also precise.
• If you take the measurement of the mass of a body of 20 kg and you get 17.4,17,17.3 and 17.1, your weighing scale is precise but not very accurate. If your scale gives you values of 19.8, 20.5, 21.0, and 19.6, it is more accurate than the first balance but not very precise.

Difference between Accuracy and Precision

In the previous few sections having discussed what each term means, let us now look at their differences.

Practice Questions

Q1) The volume of a liquid is 26 mL. A student measures the volume and finds it to be 26.2 mL, 26.1 mL, 25.9 mL, and 26.3 mL in the first, second, third, and fourth trial, respectively. Which of the following statements is true for his measurements?

a. They are neither precise nor accurate. b. They have poor accuracy. c. They have good precision. d. They have poor precision.

Answer: They have good precision.

Q2) The volume of a liquid is 20.5 mL. Which of the following sets of measurement represents the value with good accuracy? 18.6 mL, 17.8 mL, 19.6 mL, 17.2 mL 19.2 mL, 19.3 mL, 18.8 mL, 18.6 mL 18.9 mL, 19.0 mL, 19.2 mL, 18.8 mL 20.2 mL, 20.5 mL, 20.3 mL, 20.1 mL Answer: The set 20.2 mL, 20.5 mL, 20.3 mL, 20.1 mL represents the value with good accuracy.

Frequently Asked Questions – FAQs

What is meant by accuracy.

Accuracy refers to the closeness of the measured value to a standard or true value.

What is the classification of accuracy of the system?

Accuracy of the system are classified into:

State true or false: Multiple measurements or factors are needed.

What is meant by precision.

Precision is the degree to which repeated measurements under the same conditions show the same results.

What is meant by error

The difference between the actual value and the measured value is known as error.

Write the two factors to be considered while taking measurements?

What is point accuracy, can the results be precise and accurate, define reproducibility., if the player shoots ball into the goal in one shot, he is said to be accurate or precise, watch the video to find out what are base measurements.

In this article, you learnt about the concept of accuracy and precision, and you also learnt about how the differences can be seen in real life. Learn more about science, the accurate and the precise way! Download BYJU’S The Learning App.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

1.3 Accuracy, Precision, and Significant Figures

Learning objectives.

By the end of this section, you will be able to:

• Determine the appropriate number of significant figures in both addition and subtraction, as well as multiplication and division calculations.
• Calculate the percent uncertainty of a measurement.

Accuracy and Precision of a Measurement

Science is based on observation and experiment—that is, on measurements. Accuracy is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard computer paper. The packaging in which you purchased the paper states that it is 11.0 inches long. You measure the length of the paper three times and obtain the following measurements: 11.1 in., 11.2 in., and 10.9 in. These measurements are quite accurate because they are very close to the correct value of 11.0 inches. In contrast, if you had obtained a measurement of 12 inches, your measurement would not be very accurate.

The precision of a measurement system refers to how close the agreement is between repeated measurements (which are repeated under the same conditions). Consider the example of the paper measurements. The precision of the measurements refers to the spread of the measured values. One way to analyze the precision of the measurements would be to determine the range, or difference, between the lowest and the highest measured values. In that case, the lowest value was 10.9 in. and the highest value was 11.2 in. Thus, the measured values deviated from each other by at most 0.3 in. These measurements were relatively precise because they did not vary too much in value. However, if the measured values had been 10.9, 11.1, and 11.9, then the measurements would not be very precise because there would be significant variation from one measurement to another.

The measurements in the paper example are both accurate and precise, but in some cases, measurements are accurate but not precise, or they are precise but not accurate. Let us consider an example of a GPS system that is attempting to locate the position of a restaurant in a city. Think of the restaurant location as existing at the center of a bull’s-eye target, and think of each GPS attempt to locate the restaurant as a black dot. In Figure 1.23 , you can see that the GPS measurements are spread out far apart from each other, but they are centered close to the actual location of the restaurant at the center of the target. This indicates a low precision, high accuracy measuring system. However, in Figure 1.24 , the GPS measurements are concentrated quite closely to one another, but they are far away from the target location. This indicates a high precision, low accuracy measuring system.

Accuracy, Precision, and Uncertainty

The degree of accuracy and precision of a measuring system are related to the uncertainty in the measurements. Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high. In more general terms, uncertainty can be thought of as a disclaimer for your measured values. For example, if someone asked you to provide the mileage on your car, you might say that it is 45,000 miles, plus or minus 500 miles. The plus or minus amount is the uncertainty in your value. That is, you are indicating that the actual mileage of your car might be as low as 44,500 miles or as high as 45,500 miles, or anywhere in between. All measurements contain some amount of uncertainty. In our example of measuring the length of the paper, we might say that the length of the paper is 11 in., plus or minus 0.2 in. The uncertainty in a measurement, A A , is often denoted as δA δA (“delta A A ”), so the measurement result would be recorded as A ± δA A ± δA . In our paper example, the length of the paper could be expressed as 11  in. ± 0. 2 . 11  in. ± 0. 2 .

The factors contributing to uncertainty in a measurement include:

• Limitations of the measuring device,
• The skill of the person making the measurement,
• Irregularities in the object being measured,
• Any other factors that affect the outcome (highly dependent on the situation).

In our example, such factors contributing to the uncertainty could be the following: the smallest division on the ruler is 0.1 in., the person using the ruler has bad eyesight, or one side of the paper is slightly longer than the other. At any rate, the uncertainty in a measurement must be based on a careful consideration of all the factors that might contribute and their possible effects.

Making Connections: Real-World Connections – Fevers or Chills?

Uncertainty is a critical piece of information, both in physics and in many other real-world applications. Imagine you are caring for a sick child. You suspect the child has a fever, so you check their temperature with a thermometer. What if the uncertainty of the thermometer were 3 . 0º C 3 . 0º C ? If the child’s temperature reading was 37 . 0º C 37 . 0º C (which is normal body temperature), the “true” temperature could be anywhere from a hypothermic 34 . 0º C 34 . 0º C to a dangerously high 40 . 0º C 40 . 0º C . A thermometer with an uncertainty of 3 . 0º C 3 . 0º C would be useless.

Percent Uncertainty

One method of expressing uncertainty is as a percent of the measured value. If a measurement A A is expressed with uncertainty, δA δA , the percent uncertainty (%unc) is defined to be

Example 1.2

Calculating percent uncertainty: a bag of apples.

A grocery store sells 5-lb 5-lb bags of apples. You purchase four bags over the course of a month and weigh the apples each time. You obtain the following measurements:

• Week 1 weight: 4.8 lb 4.8 lb
• Week 2 weight: 5.3 lb 5.3 lb
• Week 3 weight: 4.9 lb 4.9 lb
• Week 4 weight: 5.4 lb 5.4 lb

You have previously determined, using additional measurements, that the uncertainty in the average weight of the 5-lb 5-lb bag is ± 0 . 4 lb ± 0 . 4 lb . What is the percent uncertainty of the bag’s weight, given these 4 measurements?

First, observe that the expected value of the bag’s weight, A A , is 5 lb. The uncertainty in this value, δA δA , is 0.4 lb. We can use the following equation to determine the percent uncertainty of the weight:

Plug the known values into the equation:

We can conclude that the weight of the apple bag is 5 lb ± 8 % 5 lb ± 8 % . Consider how this percent uncertainty would change if the bag of apples were half as heavy, but the uncertainty in the weight remained the same. Hint for future calculations: when calculating percent uncertainty, always remember that you must multiply the fraction by 100%. If you do not do this, you will have a decimal quantity, not a percent value.

Uncertainties in Calculations

There is an uncertainty in anything calculated from measured quantities. For example, the area of a floor calculated from measurements of its length and width has an uncertainty because the length and width have uncertainties. How big is the uncertainty in something you calculate by multiplication or division? If the measurements going into the calculation have small uncertainties (a few percent or less), then the method of adding percents can be used for multiplication or division. This method says that the percent uncertainty in a quantity calculated by multiplication or division is the sum of the percent uncertainties in the items used to make the calculation . For example, if a floor has a length of 4 . 00 m 4 . 00 m and a width of 3 . 00 m 3 . 00 m , with uncertainties of 2% 2% and 1% 1% , respectively, then the area of the floor is 12 . 0 m 2 12 . 0 m 2 and has an uncertainty of 3% 3% . (Expressed as an area this is 0 . 36 m 2 0 . 36 m 2 , which we round to 0 . 4 m 2 0 . 4 m 2 since the area of the floor is given to a tenth of a square meter.)

Check Your Understanding

A high school track coach has just purchased a new stopwatch. The stopwatch manual states that the stopwatch has an uncertainty of ±0.05 s. The team's top sprinter clocked a 100 meter sprint at 12.04 seconds last week and at 11.96 seconds this week. Can we conclude that this week's time was faster?

No, the uncertainty in the stopwatch is too great to effectively differentiate between the sprint times.

Precision of Measuring Tools and Significant Figures

An important factor in the accuracy and precision of measurements involves the precision of the measuring tool. In general, a precise measuring tool is one that can measure values in very small increments. For example, a standard ruler can measure length to the nearest millimeter, while a caliper can measure length to the nearest 0.01 millimeter. The caliper is a more precise measuring tool because it can measure extremely small differences in length. The more precise the measuring tool, the more precise and accurate the measurements can be.

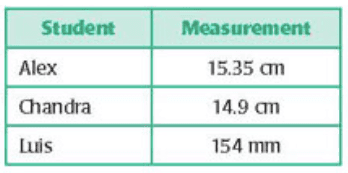
When we express measured values, we can only list as many digits as we initially measured with our measuring tool. For example, if you use a standard ruler to measure the length of a stick, you may measure it to be 36 . 7 cm 36 . 7 cm . You could not express this value as 36 . 71 cm 36 . 71 cm because your measuring tool was not precise enough to measure a hundredth of a centimeter. It should be noted that the last digit in a measured value has been estimated in some way by the person performing the measurement. For example, the person measuring the length of a stick with a ruler notices that the stick length seems to be somewhere in between 36 . 6 cm 36 . 6 cm and 36 . 7 cm 36 . 7 cm , and they must estimate the value of the last digit. Using the method of significant figures , the rule is that the last digit written down in a measurement is the first digit with some uncertainty . In order to determine the number of significant digits in a value, start with the first measured value at the left and count the number of digits through the last digit written on the right. For example, the measured value 36 . 7 cm 36 . 7 cm has three digits, or significant figures. Significant figures indicate the precision of a measuring tool that was used to measure a value.

Special consideration is given to zeros when counting significant figures. The zeros in 0.053 are not significant, because they are only placekeepers that locate the decimal point. There are two significant figures in 0.053. The zeros in 10.053 are not placekeepers but are significant—this number has five significant figures. The zeros in 1300 may or may not be significant depending on the style of writing numbers. They could mean the number is known to the last digit, or they could be placekeepers. So 1300 could have two, three, or four significant figures. (To avoid this ambiguity, write 1300 in scientific notation.) Zeros are significant except when they serve only as placekeepers .

Determine the number of significant figures in the following measurements:

• 6 × 10 3 6 × 10 3

(a) 1; the zeros in this number are placekeepers that indicate the decimal point

(b) 6; here, the zeros indicate that a measurement was made to the 0.1 decimal point, so the zeros are significant

(c) 1; the value 10 3 10 3 signifies the decimal place, not the number of measured values

(d) 5; the final zero indicates that a measurement was made to the 0.001 decimal point, so it is significant

(e) 4; any zeros located in between significant figures in a number are also significant

Significant Figures in Calculations

When combining measurements with different degrees of accuracy and precision, the number of significant digits in the final answer can be no greater than the number of significant digits in the least precise measured value . There are two different rules, one for multiplication and division and the other for addition and subtraction, as discussed below.

1. For multiplication and division: The result should have the same number of significant figures as the quantity having the least significant figures entering into the calculation . For example, the area of a circle can be calculated from its radius using A = πr 2 A = πr 2 . Let us see how many significant figures the area has if the radius has only two—say, r = 1 . 2 m r = 1 . 2 m . Then,

is what you would get using a calculator that has an eight-digit output. But because the radius has only two significant figures, it limits the calculated quantity to two significant figures or

even though π π is good to at least eight digits.

2. For addition and subtraction: The answer can contain no more decimal places than the least precise measurement . Suppose that you buy 7.56-kg of potatoes in a grocery store as measured with a scale with precision 0.01 kg. Then you drop off 6.052-kg of potatoes at your laboratory as measured by a scale with precision 0.001 kg. Finally, you go home and add 13.7 kg of potatoes as measured by a bathroom scale with precision 0.1 kg. How many kilograms of potatoes do you now have, and how many significant figures are appropriate in the answer? The mass is found by simple addition and subtraction:

Next, we identify the least precise measurement: 13.7 kg. This measurement is expressed to the 0.1 decimal place, so our final answer must also be expressed to the 0.1 decimal place. Thus, the answer is rounded to the tenths place, giving us 15.2 kg.

Significant Figures in this Text

In this text, most numbers are assumed to have three significant figures. Furthermore, consistent numbers of significant figures are used in all worked examples. You will note that an answer given to three digits is based on input good to at least three digits, for example. If the input has fewer significant figures, the answer will also have fewer significant figures. Care is also taken that the number of significant figures is reasonable for the situation posed. In some topics, particularly in optics, more accurate numbers are needed and more than three significant figures will be used. Finally, if a number is exact , such as the two in the formula for the circumference of a circle, c = 2π r c = 2π r , it does not affect the number of significant figures in a calculation.

Perform the following calculations and express your answer using the correct number of significant digits.

(a) A woman has three bags: two of the bags weigh 13.5 pounds each, and one bag weighs of 10.2 pounds. What is the total weight of the bags?

(b) The force F F on an object is equal to its mass m m multiplied by its acceleration a a . If a wagon with mass 55 kg accelerates at a rate of 0.0255  m/s 2 0.0255  m/s 2 , what is the force on the wagon? (The unit of force is called the newton, and it is expressed with the symbol N.)

(a) 37.2 pounds; Because the number of bags is an exact value, it is not considered in the significant figures.

(b) 1.4 N; Because the value 55 kg has only two significant figures, the final value must also contain two significant figures.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/1-3-accuracy-precision-and-significant-figures

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.3: Accuracy, Precision, and Significant Figures

• Last updated
• Save as PDF
• Page ID 1479

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Determine the appropriate number of significant figures in both addition and subtraction, as well as multiplication and division calculations.
• Calculate the percent uncertainty of a measurement.

Accuracy and Precision of a Measurement

Science is based on observation and experiment—that is, on measurements. Accuracy is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard computer paper. The packaging in which you purchased the paper states that it is 11.0 inches long. You measure the length of the paper three times and obtain the following measurements: 11.1 in., 11.2 in., and 10.9 in. These measurements are quite accurate because they are very close to the correct value of 11.0 inches. In contrast, if you had obtained a measurement of 12 inches, your measurement would not be very accurate.

The precision of a measurement system refers to how close the agreement is between repeated measurements (which are repeated under the same conditions). Consider the example of the paper measurements. The precision of the measurements refers to the spread of the measured values. One way to analyze the precision of the measurements would be to determine the range, or difference, between the lowest and the highest measured values. In that case, the lowest value was 10.9 in. and the highest value was 11.2 in. Thus, the measured values deviated from each other by at most 0.3 in. These measurements were relatively precise because they did not vary too much in value. However, if the measured values had been 10.9, 11.1, and 11.9, then the measurements would not be very precise because there would be significant variation from one measurement to another.

The measurements in the paper example are both accurate and precise, but in some cases, measurements are accurate but not precise, or they are precise but not accurate. Let us consider an example of a GPS system that is attempting to locate the position of a restaurant in a city. Think of the restaurant location as existing at the center of a bull’s-eye target, and think of each GPS attempt to locate the restaurant as a black dot. In Figure \(\PageIndex{3}\), you can see that the GPS measurements are spread out far apart from each other, but they are all relatively close to the actual location of the restaurant at the center of the target. This indicates a low precision, high accuracy measuring system. However, in Figure 4, the GPS measurements are concentrated quite closely to one another, but they are far away from the target location. This indicates a high precision, low accuracy measuring system.

Accuracy, Precision, and Uncertainty

The degree of accuracy and precision of a measuring system are related to the uncertainty in the measurements. Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high. In more general terms, uncertainty can be thought of as a disclaimer for your measured values. For example, if someone asked you to provide the mileage on your car, you might say that it is 45,000 miles, plus or minus 500 miles. The plus or minus amount is the uncertainty in your value. That is, you are indicating that the actual mileage of your car might be as low as 44,500 miles or as high as 45,500 miles, or anywhere in between. All measurements contain some amount of uncertainty. In our example of measuring the length of the paper, we might say that the length of the paper is 11 in., plus or minus 0.2 in. The uncertainty in a measurement, A, is often denoted as δA (“delta A”), so the measurement result would be recorded as A ± δA. In our paper example, the length of the paper could be expressed as 11 in.± 0.2.

The factors contributing to uncertainty in a measurement include:

• Limitations of the measuring device,
• The skill of the person making the measurement,
• Irregularities in the object being measured,
• Any other factors that affect the outcome (highly dependent on the situation).

In our example, such factors contributing to the uncertainty could be the following: the smallest division on the ruler is 0.1 in., the person using the ruler has bad eyesight, or one side of the paper is slightly longer than the other. At any rate, the uncertainty in a measurement must be based on a careful consideration of all the factors that might contribute and their possible effects.

MAKING CONNECTIONS: REAL-WORLD CONNECTIONS – FEVERS OR CHILLS?

Uncertainty is a critical piece of information, both in physics and in many other real-world applications. Imagine you are caring for a sick child. You suspect the child has a fever, so you check his or her temperature with a thermometer. What if the uncertainty of the thermometer were 3.0ºC? If the child’s temperature reading was 37.0ºC (which is normal body temperature), the “true” temperature could be anywhere from a hypothermic 34.0ºC to a dangerously high 40.0ºC. A thermometer with an uncertainty of 3.0ºC would be useless.

Percent Uncertainty

One method of expressing uncertainty is as a percent of the measured value. If a measurement A is expressed with uncertainty, \(δA\), the percent uncertainty (%uncertainty) is defined to be

\[\% \,\text{unc} =\dfrac {δA}{A} \times 100\%\]

Example \(\PageIndex{1}\): Calculating Percent Uncertainty: A Bag of Apples

A grocery store sells 5-lb bags of apples. You purchase four bags over the course of a month and weigh the apples each time. You obtain the following measurements:

Week 1 weight: 4.8 lb Week 2 weight: 5.3 lb Week 3 weight: 4.9 lb Week 4 weight: 5.4 lb

You determine that the weight of the 5-lb bag has an uncertainty of ±0.4lb. What is the percent uncertainty of the bag’s weight?

First, observe that the expected value of the bag’s weight, \(A\), is 5 lb. The uncertainty in this value, \(δA\), is 0.4 lb. We can use the following equation to determine the percent uncertainty of the weight:

\(\text{% unc} =\frac{δA}{A}×100%\).

Plug the known values into the equation:

\(\text{% unc} =\frac{0.4 lb}{5 lb}×100%=8%\).

We can conclude that the weight of the apple bag is \(5lb±8%\). Consider how this percent uncertainty would change if the bag of apples were half as heavy, but the uncertainty in the weight remained the same. Hint for future calculations: when calculating percent uncertainty, always remember that you must multiply the fraction by 100%. If you do not do this, you will have a decimal quantity, not a percent value.

Uncertainties in Calculations

There is an uncertainty in anything calculated from measured quantities. For example, the area of a floor calculated from measurements of its length and width has an uncertainty because the length and width have uncertainties. How big is the uncertainty in something you calculate by multiplication or division? If the measurements going into the calculation have small uncertainties (a few percent or less), then the method of adding percents can be used for multiplication or division. This method says that the percent uncertainty in a quantity calculated by multiplication or division is the sum of the percent uncertainties in the items used to make the calculation . For example, if a floor has a length of 4.00m and a width of 3.00m, with uncertainties of 2% and 1%, respectively, then the area of the floor is 12.0m2 and has an uncertainty of 3%. (Expressed as an area this is 0.36m2, which we round to \(0.4\,m^2\) since the area of the floor is given to a tenth of a square meter.)

Exercise \(\PageIndex{1}\)

A high school track coach has just purchased a new stopwatch. The stopwatch manual states that the stopwatch has an uncertainty of ±0.05s. Runners on the track coach’s team regularly clock 100-m sprints of 11.49 s to 15.01 s. At the school’s last track meet, the first-place sprinter came in at 12.04 s and the second-place sprinter came in at 12.07 s. Will the coach’s new stopwatch be helpful in timing the sprint team? Why or why not?

No, the uncertainty in the stopwatch is too great to effectively differentiate between the sprint times.

Precision of Measuring Tools and Significant Figures

An important factor in the accuracy and precision of measurements involves the precision of the measuring tool. In general, a precise measuring tool is one that can measure values in very small increments. For example, a standard ruler can measure length to the nearest millimeter, while a caliper can measure length to the nearest 0.01 millimeter. The caliper is a more precise measuring tool because it can measure extremely small differences in length. The more precise the measuring tool, the more precise and accurate the measurements can be.

When we express measured values, we can only list as many digits as we initially measured with our measuring tool. For example, if you use a standard ruler to measure the length of a stick, you may measure it to be 36.7cm. You could not express this value as 36.71cm because your measuring tool was not precise enough to measure a hundredth of a centimeter. It should be noted that the last digit in a measured value has been estimated in some way by the person performing the measurement. For example, the person measuring the length of a stick with a ruler notices that the stick length seems to be somewhere in between 36.6cm and 36.7cm, and he or she must estimate the value of the last digit. Using the method of significant figures, the rule is that the last digit written down in a measurement is the first digit with some uncertainty. In order to determine the number of significant digits in a value, start with the first measured value at the left and count the number of digits through the last digit written on the right. For example, the measured value 36.7cm has three digits, or significant figures. Significant figures indicate the precision of a measuring tool that was used to measure a value.

Special consideration is given to zeros when counting significant figures. The zeros in 0.053 are not significant, because they are only placekeepers that locate the decimal point. There are two significant figures in 0.053. The zeros in 10.053 are not placekeepers but are significant—this number has five significant figures. The zeros in 1300 may or may not be significant depending on the style of writing numbers. They could mean the number is known to the last digit, or they could be placekeepers. So 1300 could have two, three, or four significant figures. (To avoid this ambiguity, write 1300 in scientific notation.) Zeros are significant except when they serve only as placekeepers .

Exercise \(\PageIndex{2}\)

Determine the number of significant figures in the following measurements:

• × 10 3
• 1; the zeros in this number are placekeepers that indicate the decimal point
• 6; here, the zeros indicate that a measurement was made to the 0.1 decimal point, so the zeros are significant
• 1; the value 3 signifies the decimal place, not the number of measured values
• 5; the final zero indicates that a measurement was made to the 0.001 decimal point, so it is significant
• 4; any zeros located in between significant figures in a number are also significant

Significant Figures in Calculations

When combining measurements with different degrees of accuracy and precision, the number of significant digits in the final answer can be no greater than the number of significant digits in the least precise measured value . There are two different rules, one for multiplication and division and the other for addition and subtraction, as discussed below.

1. For multiplication and division: The result should have the same number of significant figures as the quantity having the least significant figures entering into the calculation. For example, the area of a circle can be calculated from its radius using A=πr2. Let us see how many significant figures the area has if the radius has only two—say, r=1.2m. Then,

\[A=πr2=(3.1415927...)×(1.2m)^2=4.5238934\,m^2\]

is what you would get using a calculator that has an eight-digit output. But because the radius has only two significant figures, it limits the calculated quantity to two significant figures or

\[A=4.5\,m^2,\]

even though \( is good to at least eight digits.

2. For addition and subtraction: The answer can contain no more decimal places than the least precise measurement. Suppose that you buy 7.56-kg of potatoes in a grocery store as measured with a scale with precision 0.01 kg. Then you drop off 6.052-kg of potatoes at your laboratory as measured by a scale with precision 0.001 kg. Finally, you go home and add 13.7 kg of potatoes as measured by a bathroom scale with precision 0.1 kg. How many kilograms of potatoes do you now have, and how many significant figures are appropriate in the answer? The mass is found by simple addition and subtraction:

kg − 6.052\, kg + 13.7\, kg \, 15.208\, kg = 15.2\, kg .\]

Next, we identify the least precise measurement: 13.7 kg. This measurement is expressed to the 0.1 decimal place, so our final answer must also be expressed to the 0.1 decimal place. Thus, the answer is rounded to the tenths place, giving us 15.2 kg.

Significant Figures in this Text

In this text, most numbers are assumed to have three significant figures. Furthermore, consistent numbers of significant figures are used in all worked examples. You will note that an answer given to three digits is based on input good to at least three digits, for example. If the input has fewer significant figures, the answer will also have fewer significant figures. Care is also taken that the number of significant figures is reasonable for the situation posed. In some topics, particularly in optics, more accurate numbers are needed and more than three significant figures will be used. Finally, if a number is exact , such as the two in the formula for the circumference of a circle, \( = 2 π r ,\) it does not affect the number of significant figures in a calculation.

Exercise \(\PageIndex{3}\)

Perform the following calculations and express your answer using the correct number of significant digits.

• A woman has two bags weighing 13.5 pounds and one bag with a weight of 10.2 pounds. What is the total weight of the bags?
• The force \(F\) on an object is equal to its mass m multiplied by its acceleration \(a\). If a wagon with mass 55 kg accelerates at a rate of \(0.0255 m/s^2\), what is the force on the wagon? (The unit of force is called the newton, and it is expressed with the symbol N.)

(a) 37.2 pounds; Because the number of bags is an exact value, it is not considered in the significant figures.

(b) 1.4 N; Because the value 55 kg has only two significant figures, the final value must also contain two significant figures.

PHET EXPLORATIONS: ESTIMATION

Explore size estimation in one, two, and three dimensions! Multiple levels of difficulty allow for progressive skill improvement.

• Accuracy of a measured value refers to how close a measurement is to the correct value. The uncertainty in a measurement is an estimate of the amount by which the measurement result may differ from this value.
• Precision of measured values refers to how close the agreement is between repeated measurements.
• The precision of a measuring tool is related to the size of its measurement increments. The smaller the measurement increment, the more precise the tool.
• Significant figures express the precision of a measuring tool.
• When multiplying or dividing measured values, the final answer can contain only as many significant figures as the least precise value.
• When adding or subtracting measured values, the final answer cannot contain more decimal places than the least precise value.

Contributors and Attributions

Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a  Creative Commons Attribution License (by 4.0) .

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

What Is the Difference Between Accuracy and Precision?

Accuracy and precision are two important concepts in science. Both terms apply to any experimental measurement you make. But what do they actually mean? What is the difference between them and which is more important?

What Is Accuracy?

Accuracy is a measure of how closely your experimental measurements agree with known values. The closer your measurements are to the known value, the more accurate the measurement.

If you think of the known value as the bullseye on a target, accurate shots (or measurements) mean the average of your shots is at or near the bullseye. The shots in this picture are accurate, but they are all over the target. This brings up the concept of precision.

What Is Precision?

Precision is a measure of how close your experimental measurements agree with each other. The closer each measurement is to the other measurements, the more precise your measurement.

If the measurements were shots in a target, the closer the holes are to each other, the more precise the shots. Here, the shots are all clustered together. They would be considered a precise collection of shots. The only problem is they are not very accurate.

How to Control Accuracy and Precision

Both accuracy and precision are the goal of any measurement. Variations in accuracy and precision are largely controllable.

In target shooting, you improve accuracy by moving closer to the target, or using an aiming aid like a scope or laser pointer. You improve precision by mounting your gun to a table or bench or shooting indoors out of the wind.

In a lab, improve accuracy and precision by using the same procedure taking each measurement and using tools designed for measurements. For example, you get a more accurate and precise volume measurement using a graduated cylinder than you do using a water glass.

In general, use good tools designed for the measurement you are trying to make and pay close attention to what you are doing when you use them. This helps any measurement you make.

Which Is More Important? Accuracy or Precision?

Accuracy is more important when trying to hit a target. You either hit your target or you don’t. It does no good to be precise if you miss all your shots. You can improve accuracy in future measurements by factoring in a correction factor. If your shots are all going to the left, alter your aim to the right. Accuracy is something you can fix in future measurements.

Precision is more important in calculations. When using a measured value in a calculation, you can only be as precise as your least precise measurement. This is the main idea behind the topic of significant figures  in calculations. You can improve precision by using a better measuring tool and/or improving your skill at using the tool.

Accuracy and precision are both important to good measurements in science. Try to make the best of both in all your measurements. But, no matter how hard you try, measurements always deviate slightly from true values. This is because of error .

Related Posts

• Measurement Practice
• Significant Digit Practice
• Calculation with Sig. Dig.
• Exploring Density

Measurement

• Handout : Condensed notes for Measurement Unit
• Film : Measurement of Flouride Video Clip
• Homework : Read article on the loss of the Mars Orbiter
• Units/Scientific Notation
• Accuracy vs. Precision
• Lab : Measure various objects with different rulers, balances, and cylinders.
• Computer Lab : Practice taking measurements with correct precision.
• Homework : Rulers and Cylinders Practice
• Computer Lab : Practice Counting Significant Digits
• Homework : Units, Precision, and Scientific Notation Sheet
• Computer Lab : Practice Calculating With Significant Digits
• Homework : Calculations with Significant Digits .
• Homework : Label Factoring Practice Sheet
• Homework : Conversions Sheet
• Compuer Lab : Exploring Density
• Lab : Density of Various Objects
• Homework : Lab Questions from Density of Various Objects Lab
• Handout : Putting Data in lab Format
• Lab : Measuring the Thickness of Aluminum Foil: Given three different pieces of foil (generic standard foil, name brand standard foil, and name brand heavy duty foil) determine their thicknesses. You should find at least 2 ways to determine this thickness using only a ruler, a balance, and anything else in your lab drawers. One method for determining the thickness must take into consideration the density of aluminum 2.70g/cm 3.
• Homework : Write up the Foil calculations in correct lab format and give a numerical conclusion about the thickness of each piece of foil.
• Handout : ClarisWorks spreadsheet tutorial.
• Handout : How to create proper graphs.
• Handout : Graphical Analysis software tutorial.
• Handout : Writing a Lab Report.
• Handout : Shorthand remarks I use when correcting your labs.
• Homework : Type a full lab write up for the Coke vs. Diet Coke lab.
• Homework : Review Practice Sheet

Accuracy and Precision

Quiz   by ashley brady.

Feel free to use or edit a copy

includes Teacher and Student dashboards

Measure skills from any curriculum

Tag the questions with any skills you have. Your dashboard will track each student's mastery of each skill.

• edit the questions
• save a copy for later
• start a class game
• automatically assign follow-up activities based on students’ scores
• assign as homework
• share a link with colleagues
• print as a bubble sheet

Our brand new solo games combine with your quiz, on the same screen

Correct quiz answers unlock more play!

• Q 2 ______________ refers to how close the measurement is to the true or accepted value accuracy 30 s
• Q 3 ______________________ refers to how close a group of measurements are to each other precision 30 s
• Q 4 Accuracy is the closeness of a measurement to the true value. the closeness of measurements to each other 30 s
• Q 5 Precision is... how close a set of measurements are to each other the closeness of a measurement to the true value 30 s
• Q 6 Measurements will be close together and close to the accepted value. neither accurate or precise precise but not accurate accurate but not precise accurate & precise 30 s
• Q 7 Measurements will be close together, not close to the accepted value. accurate but not precise neither accurate or precise both accurate and precise precise but not accurate 30 s
• Q 8 Measurements will be random. precise but not accurate both accurate and precise neither accurate or precise accurate but not precise 30 s
• Q 9 If given the data set below determine if it is accurate/precise/both/neither: 32, 33, 32, 31 (Accepted value = 45) accurate but not precise both accurate and precise neither accurate or precise precise but not accurate 30 s
• Q 12 If given the data set below determine if it is accurate/precise/both/neither: 7, 6, 6, 5 (Accepted Value = 6) both accurate and precise precise but not accurate neither accurate or precise accurate but not precise 30 s
• Q 13 If given the data set below determine if it is accurate/precise/both/neither: 119, 32, 21, 57 (Accepted value = 25) neither precise or accurate accurate but not precise precise but not accurate both accurate and precise 30 s
• Q 14 Romy's measurements: 6.02 m, 6. 04 m, 6.03 m Actual Value: 6.02 m How would you define her measurements? accurate but not precise precise but not accurate neither accurate or precise both accurate and precise 30 s

Teachers give this quiz to your class

Chemistry: Accuracy, Precision, & Measurement-Print/Digital |Distance Learning

What educators are saying

Also included in.

Description

Updated: Now includes print and digital options for the lesson. Perfect for distance learning or the paperless classroom. Interactive student notes, exit ticket, and homework for Google Slides™.

In this complete lesson, students will differentiate between accuracy and precision. Accuracy will be related to percentage error, and precision is related to the precision of the measuring instrument. Students will accurately record measurements for mass, liquid volume, temperature, and length. A class activity is described in the teacher notes .

You will notice that within this lesson the words significant figures are not used. This is very important! In order for students to accept that significant figures are not just some torture devise concocted by chemistry teachers, they must have a firm understanding of the importance of sig figs. And, we establish this importance by teaching proper measurement first! At this level, the main focus on measurement is how to record the measurement properly so that anyone that reads the measurement will know the precision of the measuring instrument used.

The main concept of this lesson is precision! Some teachers just teach the dart board analogy, and leave it at that. But this is totally missing the whole point of precision!! By learning the precision of the different measurement tools, and how to correctly record that precision, students will now be in the frame of mind to accept significant figures, in the next lesson, as recording measurement in a standard way that’s used throughout the scientific community.

Lesson Objectives:

• Differentiate between and define accuracy and precision
• Correctly use scientific measuring tools including: electronic balance, triple beam balance, graduated cylinder, lab thermometer, metric ruler, and meter stick
• Correctly record a measurement showing the precision of the measurement tool
• Calculate percentage error

Prior Knowledge:

Basic middle school and high school physical science

Lesson Duration: 1 – 1 ½ class periods depending on discussion and class activity.

Included in This Resource

• PowerPoint-–editable and animated
• Student Notes- Cornell style– Cloze notes
• Student Notes – Blank
• Suggested KEY for Student Notes
• Teacher Notes (3 pages) includes background info, slide-by-slide notes, & a class activity
• Homework Assignment w/ KEY
• Exit Ticket w/ KEY

Teacher Prep Time: Just print and go!

Note on the PowerPoints: The PowerPoints included in this product are editable. They are also animated, which means that they may appear busy or overlapping in the slide edit mode, but will be awesome in the slide show mode! Please don’t edit the PowerPoints until you have seen them in the slide show mode!

This lesson is appropriate for grades 9-12 chemistry & physical science

This will be a lesson you will want to use year after year!

Chemistry Corner

**************************************************************************************

Check out these other products that you may be interested in:

Introduction to Chemistry Lab Unit Bundle

Introduction to Chemistry Mega Unit Bundle

Chemistry Task Cards for the Year – A Growing Bundle

BellWork/WarmUps Editable For the Entire Year: Chemistry

Chemistry Doodle Notes for the Year: A Growing Bundle

High School Chemistry Year Curriculum

*************************************************************************************

Get TPT credit to use on your Future Purchases!

Go to your “My Purchases” page and click on “Provide Feedback” button. Your feedback is greatly appreciated! Click HERE for more information.

Become a follower to receive updates about new products as I add them.

Chemistry Corner’s PowerPoints are perfect for the flipped classroom . However, please read the Copyright Terms below before using it as such. Thanks!

LICENSING TERMS: By downloading this product, you own a license for one teacher only for personal use in your classroom. Licenses are non-transferable, meaning they cannot be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. I you are a coach, principal or district interested in transferable licenses to accommodate yearly staff changes, please contact TpT for Schools at [email protected] or find more information under “Schools” on the Teachers Pay Teachers site.

COPYRIGHT TERMS: ©Chemistry Corner. Please note – all material included in this resource belongs to Chemistry Corner. By downloading, you have a license to use the material, but you do not own the material. This resource, or any portion of this resource, may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students —no other teachers or anyone else on the internet.

Questions & Answers

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think